
【题目】如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.
【答案】
(1)证明:由尺规作∠BAF的角平分线的过程可得AB=AF,∠BAE=∠FAE,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠FAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=FA,
∴四边形ABEF为平行四边形,
∵AB=AF,
∴四边形ABEF为菱形;
(2)解:∵四边形ABEF为菱形,
∴AE⊥BF,BO= ![]() FB=3,AE=2AO,
FB=3,AE=2AO,
在Rt△AOB中,AO= ![]() =4,
=4,
∴AE=2AO=8.
【解析】(1)由尺规作图和已知先证出BE=FA,再由一组对边平行且相等的四边形可得四边形ABEF为平行四边形,又AB=AF可得证;
(2)由菱形的性质易求出BO=3和∠AOB=90°,在Rt△AOB中可求出AO的值,再由菱形的性质可求出AE的长.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.


 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是平行四边形,点C在x轴上,反比例函数y= ![]() (x>0)的图象经过点A(5,12),且与边BC交于点D.若AB=BD,则点D的坐标为 .
(x>0)的图象经过点A(5,12),且与边BC交于点D.若AB=BD,则点D的坐标为 . 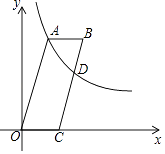
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
小明遇到这样问题:
如图1,在![]() 中,
中,![]() ,在AB上取一点D,在AC延长线上取一点E,若
,在AB上取一点D,在AC延长线上取一点E,若![]() ,判断PD与PE的数量关系.
,判断PD与PE的数量关系.
小明通过思考发现,可以采用两种方法解决向题:
方法一:过点D作![]() ,交BC于F,即可解决向题;
,交BC于F,即可解决向题;
方法二:过点D、点E分别向直线BC引垂钱,垂足分别是F、G,也可解决问题.
![]() 请回答:PD与PE的数量关系是______;
请回答:PD与PE的数量关系是______;
![]() 任选上述两种方法中的一种方法,在图1中补全图象,并给出证明;
任选上述两种方法中的一种方法,在图1中补全图象,并给出证明;
参考小明思考问题的方法,解决问题:
![]() 如图2,在
如图2,在![]() 中,
中,![]() ,将AC绕点A顺时针旋转
,将AC绕点A顺时针旋转![]() 度后得到AD,过点D作
度后得到AD,过点D作![]() ,交AB于点E,
,交AB于点E,![]() ,则图中是否存在与DE相等的线段,请找出来并给出证明.
,则图中是否存在与DE相等的线段,请找出来并给出证明.
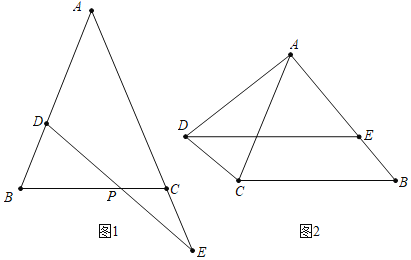
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3(a≠0)过A(4,4),B (2,m)两点,点B到抛物线对称轴的距离记为d,满足0<d≤1,则实数m的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列调查方式中,较为合适的调查方式是( )
A. 为了解深圳市中小学生的视力情况,采用普查的方式
B. 为了解深圳市中小学生的课外阅读习惯情况,采用普査的方式
C. 为了解某校七年级![]() 班学生期末考试数学成绩情况,采用抽样调査的方式
班学生期末考试数学成绩情况,采用抽样调査的方式
D. 为了解深圳市中小学生参加“课外兴趣班”报名情况,采用抽样调查的方式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为原点,点A(﹣![]() ,0),点B(0,1)把△ABO绕点O顺时针旋转,得△A'B'O,点A,B旋转后的对应点为A',B',记旋转角为α(0°<α<360°).
,0),点B(0,1)把△ABO绕点O顺时针旋转,得△A'B'O,点A,B旋转后的对应点为A',B',记旋转角为α(0°<α<360°).
(1)如图①,当点A′,B,B′共线时,求AA′的长.
(2)如图②,当α=90°,求直线AB与A′B′的交点C的坐标;
(3)当点A′在直线AB上时,求BB′与OA′的交点D的坐标(直接写出结果即可)
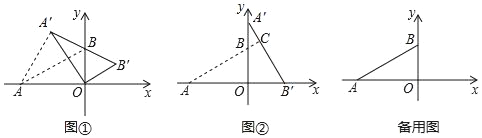
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,点P从点A出发,沿折线ABCD方向以3cm/s的速度匀速运动;点Q从点D出发,沿线段DC方向以2cm/s的速度匀速运动. 已知两点同时出发,当一个点到达终点时,另一点也停止运动,设运动时间为t(s).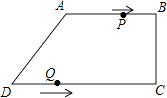
(1)求CD的长;
(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;
(3)在点P、Q的运动过程中,是否存在某一时刻,使得△BPQ的面积为20cm2?若存在,请求出所有满足条件的t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=50°,P是BC边上一点,将△ABP绕点A逆时针旋转50°,点P旋转后的对应点为点P′.
(1)画出旋转后的三角形;
(2)连接PP′,若∠BAP=20°,求∠PP′C的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() ;
;
(2)先化简![]() ,再选一个你喜欢的数求值.
,再选一个你喜欢的数求值.
(1)(﹣2016)0+| ![]() ﹣2|+
﹣2|+ ![]() +3tan30°
+3tan30°
(2)先化简(a2﹣a)÷ ![]() ,再选一个你喜欢的数求值.
,再选一个你喜欢的数求值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com