
【题目】如图,△ABC中,AB=AC,∠BAC=50°,P是BC边上一点,将△ABP绕点A逆时针旋转50°,点P旋转后的对应点为点P′.
(1)画出旋转后的三角形;
(2)连接PP′,若∠BAP=20°,求∠PP′C的度数.

【答案】(1)画图见解析;(2)∠PP′C=30°.
【解析】
(1)如图,作∠PAP′=50°,且AP=AP′,连接PP′,△ACP′即为所求;(2),连接PP′,由旋转的性质可得,∠PAP′=∠BAC=50°,AP=AP′,△ABP≌△ACP′,根据等腰三角形的性质及三角形的内角和定理可得∠APP′=∠AP′P=65°,根据全等三角形的性质可得∠AP′C=∠APB,在△ABC中,∠BAC=50°,AB=AC,可求得∠B=65°,再由∠BAP=20°,根据三角形的内角和定理求得∠APB=95°=∠AP′C,所以∠PP′C=∠AP′C-∠AP′P=30°.
(1)旋转后的△ACP′如图所示.
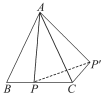
(2)如图,连接PP′.
由旋转可得,∠PAP′=∠BAC=50°,AP=AP′,△ABP≌△ACP′,
∴∠APP′=∠AP′P=65°,∠AP′C=∠APB,
∵∠BAC=50°,AB=AC,
∴∠B=65°,
又∵∠BAP=20°,
∴∠APB=95°=∠AP′C,
∴∠PP′C=∠AP′C-∠AP′P=95°-65°=30°.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AE是△ABC的外角∠CAD的平分线.
(1)若AE∥BC,如图1,试说明∠B=∠C;
(2)若AE交BC的延长线于点E,如图2,直接写出反应∠B、∠ACB、∠AEC之间关系的等式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前,我市城市居民用电收费方式有以下两种:
普通电价付费方式:全天0. 52元/度;
峰谷电价付费方式:峰时(早8:00~晚21:00)0. 65元/度;谷时(晚21:00~早8:00)0. 40元/度.
(1)小丽老师家10月份总用电量为280度.
①若其中峰时电量为80度,则小丽老师家按照哪种方式付电费比较合适?能省多少元?
②若小丽老师交费137元,那么,小丽老师家峰时电量为多少度?
(2)到11月份付费时,小丽老师发现11月份总用电量为320度,用峰谷电价付费方式比普通电价付费方式省了18. 4元,那么,11月份小丽老师家峰时电量为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光合作用是指绿色植物通过叶绿体,利用光能,把二氧化碳和水转化成储存能量的有机物,并释放出氧气的过程.如图是夏季的白天7时~18时的一般的绿色植物的光合作用强度与时间之间的关系的曲线,分析图象回答问题:
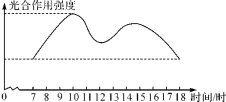
(1)大约几时的光合作用最强?大约几时的光合作用最弱?
(2)说一说绿色植物光合作用的强度从7时到18时是怎样变化的.
查看答案和解析>>
科目:初中数学 来源: 题型:
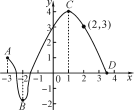
【题目】已知两个变量x,y之间的变化情况如图所示,根据图象回答下列问题:
(1)写出y的变化范围;
(2)求当x=0,-3时,y的对应值;
(3)求当y=0,3时,对应的x的值;
(4)当x为何值时,y的值最大?
(5)当x在什么范围内时,y的值在不断增加?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016年“双十一”期间,某快递公司计划租用甲、乙两种车辆快递货物,从货物量来计算:若租用两种车辆合运,10天可以完成任务;若单独租用乙种车辆,完成任务的天数是单独租用甲种车辆完成任务天数的2倍.
(1)求甲、乙两种车辆单独完成任务分别需要多少天?
(2)已知租用甲、乙两种车辆合运需租金65000元,甲种车辆每天的租金比乙种车辆每天的租金多1500元,试问:租甲和乙两种车辆、单独租甲种车辆、单独租乙种车辆这三种租车方案中,哪一种租金最少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=AC=AD,AC平分∠BAD,点P是AC延长线上一点,且PD⊥AD. 
(1)证明:∠BDC=∠PDC;
(2)若AC与BD相交于点E,AB=1,CE:CP=2:3,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com