
【题目】如图,直线l过正方形ABCD的顶点B,点A,C到直线l的距离AE,CF分别为5和3,则正方形ABCD的面积是________.

【答案】34
【解析】
由ABCD为正方形得到AB=BC,∠ABC为直角,再由AE与CF都垂直于EF,利用同角的余角相等得到一对角相等,再由一对直角相等,;利用AAS得出三角形ABE与三角形BCF全等,由全等三角形对应边相等得到AE=BF,EB=CF,在直角三角形ABE中,利用勾股定理求出AB的长,即可确定出正方形的面积.
∵ABCD为正方形,
∴AB=BC,∠ABC=90°,
∵AE⊥EF,CF⊥EF,
∴∠AEB=∠BFC=90°,
∴∠BAE+∠ABE=90°,∠ABE+∠CBF=90°,
∴∠BAE=∠CBF,
在△ABE和△BCF中,
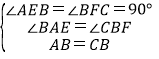 ,
,
∴△ABE≌△BCF(AAS),
∴AE=BF=5,CF=EB=3,
根据勾股定理得:AB=![]() =
=![]() ,
,
则正方形ABCD面积为34.
故答案为:34


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.
(1)求证:△ABE≌△DAF;
(2)若AF=1,四边形ABED的面积为6,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是平行四边形,点C在x轴上,反比例函数y= ![]() (x>0)的图象经过点A(5,12),且与边BC交于点D.若AB=BD,则点D的坐标为 .
(x>0)的图象经过点A(5,12),且与边BC交于点D.若AB=BD,则点D的坐标为 . 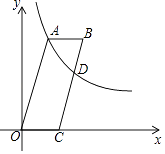
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店购进一批甲、乙两种款型时尚T恤衫,甲种款型共用了7800元,乙种款型共用了6400元,甲种款型的件数是乙种款型件数的1.5倍,甲种款型每件的进价比乙种款型每件的进价少30元.
(1)甲、乙两种款型的T恤衫各购进多少件?
(2)商店进价提高60%标价销售,销售一段时间后,甲款型全部售完,乙款型剩余一半,商店决定对乙款型按标价的五折降价销售,很快全部售完,求售完 这批T恤衫商店共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
小明遇到这样问题:
如图1,在![]() 中,
中,![]() ,在AB上取一点D,在AC延长线上取一点E,若
,在AB上取一点D,在AC延长线上取一点E,若![]() ,判断PD与PE的数量关系.
,判断PD与PE的数量关系.
小明通过思考发现,可以采用两种方法解决向题:
方法一:过点D作![]() ,交BC于F,即可解决向题;
,交BC于F,即可解决向题;
方法二:过点D、点E分别向直线BC引垂钱,垂足分别是F、G,也可解决问题.
![]() 请回答:PD与PE的数量关系是______;
请回答:PD与PE的数量关系是______;
![]() 任选上述两种方法中的一种方法,在图1中补全图象,并给出证明;
任选上述两种方法中的一种方法,在图1中补全图象,并给出证明;
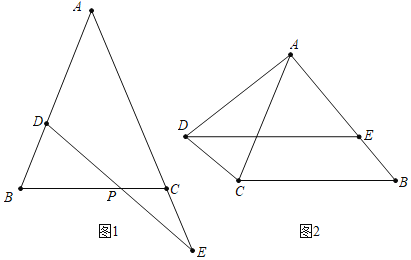
参考小明思考问题的方法,解决问题:
![]() 如图2,在
如图2,在![]() 中,
中,![]() ,将AC绕点A顺时针旋转
,将AC绕点A顺时针旋转![]() 度后得到AD,过点D作
度后得到AD,过点D作![]() ,交AB于点E,
,交AB于点E,![]() ,则图中是否存在与DE相等的线段,请找出来并给出证明.
,则图中是否存在与DE相等的线段,请找出来并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3(a≠0)过A(4,4),B (2,m)两点,点B到抛物线对称轴的距离记为d,满足0<d≤1,则实数m的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=50°,P是BC边上一点,将△ABP绕点A逆时针旋转50°,点P旋转后的对应点为点P′.
(1)画出旋转后的三角形;
(2)连接PP′,若∠BAP=20°,求∠PP′C的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com