
【题目】张庄甲、乙两家草莓采摘园的草莓销售价格相同,“春节期间”,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为![]() (千克),在甲园所需总费用为
(千克),在甲园所需总费用为![]() (元),在乙园所需总费用为
(元),在乙园所需总费用为![]() (元),
(元),![]() 、
、![]() 与
与![]() 之间的函数关系如图所示,折线OAB表示
之间的函数关系如图所示,折线OAB表示![]() 与
与![]() 之间的函数关系.
之间的函数关系.

(1)甲采摘园的门票是 元,两个采摘园优惠前的草莓单价是每千克 元;
(2)当![]() >10时,求
>10时,求![]() 与
与![]() 的函数表达式;
的函数表达式;
(3)游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.
【答案】(1)60,30;(2)y乙=12x+180;(3)采摘5千克或20千克草莓时,甲、乙两家采摘园的总费用相同.
【解析】
(1)(1)根据函数图象可以求得草莓销售价格是每千克的钱数和甲基地的门票;
(2)![]() 与x的函数表达式结合图象利用待定系数法即可解决;
与x的函数表达式结合图象利用待定系数法即可解决;
(3)求出![]() 函数表达式=60+单价×数量,甲、乙两家采摘园的总费用相同即
函数表达式=60+单价×数量,甲、乙两家采摘园的总费用相同即![]() =
=![]() .
.
解:(1)甲、采摘园优惠前的草莓销售价格是每千克![]() =30元.
=30元.
由图像知甲基地的门票是60元/人,
故答案为:30,60;
(2)当x>10时,设![]() =kx+b.
=kx+b.
把点(10,300),(25,480)分别代入,得
![]() ,
,
解得![]() ,
,
当x>10时,![]() =12x+180.
=12x+180.
(3)![]() =30×0.6x+60=18x+60.
=30×0.6x+60=18x+60.
当0<x≤10时,![]() =30x.
=30x.
∴30x=18x+60,解得x=5.
当x>10时,12x+180=18x+60,解得x=20.
∴采摘5千克或20千克草莓时,甲、乙两家采摘园的总费用相同.


科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,点A,B的横坐标分别为a、a+2,二次函数y=﹣x2+(m﹣2)x+2m的图象经过点A,B,且a、m满足2a﹣m=d(d为常数).
(1)若一次函数y1=kx+b的图象经过A、B两点.
①当a=1、d=﹣1时,求k的值;
②若y1随x的增大而减小,求d的取值范围;
(2)当d=﹣4且a≠﹣2、a≠﹣4时,判断直线AB与x轴的位置关系,并说明理由;
(3)点A,B的位置随着a的变化而变化,设点A,B运动的路线与y轴分别相交于点C,D,线段CD的长度会发生变化吗?如果不变,求出CD的长;如果变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校最近发布了新的学生午休方案,为了了解学生方案的了解程度,小明和小颖一起对该学校的学生进行了抽样调査,小明将结果整理后绘制成条形统计图(如图)(A代表“完全清楚”,B代表“知道一些”,C代表,“完全不了解”):
(1)这次抽样调查了______人;
(2)小颖将调查结果绘制成扇形统计图,那么扇形统计图中C部分,对应的扇形的圆心角是多少度?
(3)若该学校一共有1000名学生,则根据此次调查,“完全清楚”的学生大约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四根小木棒,它们的长度分别为5 cm,8 cm,12 cm,13 cm,从中选出三根作为一个三角形的三边,如果所构成的三角形为直角三角形,请回答下列问题:
(1)你所选三根木棒的长度分别为多少?请说明理由;
(2)求你所构成的直角三角形斜边上的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AB的中点,点D在线段CB上.
![]()
(1)图中共有 条线段.
(2)图中AD=AC+CD,BC=AB﹣AC,类似地,请你再写出两个有关线段的和与差的关系式:
① ;② .
(3)若AB=8,DB=1.5,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,已知点A(﹣3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4、…,△16的直角顶点的坐标为( )
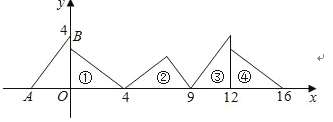
![]()
A. (60,0) B. (72,0) C. (67![]() ,
,![]() ) D. (79
) D. (79![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图象(折线OEFPMN)描述了某汽车在行驶过程中速度与时间的函数关系,下列说法中错误的是( )

A. 第3分时汽车的速度是40千米/时
B. 第12分时汽车的速度是0千米/时
C. 从第3分到第6分,汽车行驶了120千米
D. 从第9分到第12分,汽车的速度从60千米/时减少到0千米/时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.
(1)作出△ABC关于y轴对称的△A1B1C1,并写出点C1的坐标 ;
(2)在(1)的条件下,连接CC1交AB于点D,请标出点D,并直接写出CD的长.
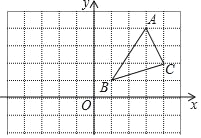
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是双曲线y= ![]() 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 . 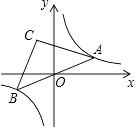
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com