
【题目】平面直角坐标系xOy中,点A,B的横坐标分别为a、a+2,二次函数y=﹣x2+(m﹣2)x+2m的图象经过点A,B,且a、m满足2a﹣m=d(d为常数).
(1)若一次函数y1=kx+b的图象经过A、B两点.
①当a=1、d=﹣1时,求k的值;
②若y1随x的增大而减小,求d的取值范围;
(2)当d=﹣4且a≠﹣2、a≠﹣4时,判断直线AB与x轴的位置关系,并说明理由;
(3)点A,B的位置随着a的变化而变化,设点A,B运动的路线与y轴分别相交于点C,D,线段CD的长度会发生变化吗?如果不变,求出CD的长;如果变化,请说明理由.
【答案】
(1)解:①当a=1、d=﹣1时,m=2a﹣d=3,
所以二次函数的表达式是y=﹣x2+x+6.
∵a=1,
∴点A的横坐标为1,点B的横坐标为3,
把x=1代入抛物线的解析式得:y=6,把x=3代入抛物线的解析式得:y=0,
∴A(1,6),B(3,0).
将点A和点B的坐标代入直线的解析式得: ![]() ,解得:
,解得: ![]() ,
,
所以k的值为﹣3.
②∵y=﹣x2+(m﹣2)x+2m=﹣(x﹣m)(x+2),
∴当x=a时,y=﹣(a﹣m)(a+2);当x=a+2时,y=﹣(a+2﹣4)(a+4),
∵y1随着x的增大而减小,且a<a+2,
∴﹣(a﹣m)(a+2)>﹣(a+2﹣m)(a+4),解得:2a﹣m>﹣4,
又∵2a﹣m=d,
∴d的取值范围为d>﹣4.
(2)解:∵d=﹣4且a≠﹣2、a≠﹣4,2a﹣m=d,
∴m=2a+4.
∴二次函数的关系式为y=﹣x2+(2a+2)x+4a+8.
把x=a代入抛物线的解析式得:y=a2+6a+8.
把x=a+2代入抛物线的解析式得:y=a2+6a+8.
∴A(a,a2+6a+8)、B(a+2,a2+6a+8).
∵点A、点B的纵坐标相同,
∴AB∥x轴.
(3)解:线段CD的长度不变.
∵y=﹣x2+(m﹣2)x+2m过点A、点B,2a﹣m=d,
∴y=﹣x2+(2a﹣d﹣2)x+2(2a﹣d).
∴yA=﹣a2+(2﹣d)a﹣2d,yB=a2+(2﹣d)a﹣4d﹣8.
∵把a=0代入yA=﹣a2+(2﹣d)a﹣2d,得:y=﹣2d,
∴C(0,﹣2d).
∵点D在y轴上,即a+2=0,
∴a=﹣2,.
把a=﹣2代入yB=a2+(2﹣d)a﹣4d﹣8得:y=﹣2d﹣8.
∴D(0,﹣2d﹣8).
∴DC=|﹣2d﹣(﹣2d﹣8)|=8.
∴线段CD的长度不变.
【解析】(1)当a=1、d=﹣1时,m=2a﹣d=3,代入抛物线解析式算出A、B坐标,再代入直线解析式即可;(2)由A、B在抛物线上,得出A、B的含参数a 坐标,纵坐标相同,可判断与x轴平行;(3)分别用a 代数式表示C、D坐标,纵坐标的差是常数8,说明不变.
【考点精析】根据题目的已知条件,利用函数关系式和确定一次函数的表达式的相关知识可以得到问题的答案,需要掌握用来表示函数关系的数学式子叫做函数解析式或函数关系式;确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面内,线段AB=6,P为线段AB上的动点,三角形纸片CDE的边CD所在的直线与线段AB垂直相交于点P,且满足PC=PA.若点P沿AB方向从点A运动到点B,则点E运动的路径长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB>∠ABC.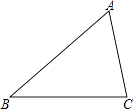
(1)用直尺和圆规在∠ACB的内部作射线CM,使∠ACM=∠ABC(不要求写作法,保留作图痕迹);
(2)若(1)中的射线CM交AB于点D,AB=9,AC=6,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=12cm,C为AB延长线上一点,CP与⊙O相切于点P,过点B作弦BD∥CP,连接PD.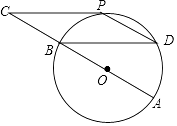
(1)求证:点P为 ![]() 的中点;
的中点;
(2)若∠C=∠D,求四边形BCPD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
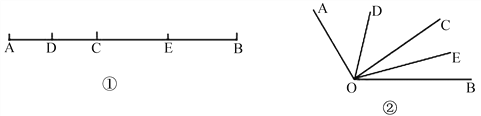
【题目】如图①,已知线段AB=12cm,点C为线段AB上的一个动点,点D、E分别是AC和BC的中点.
(1)若点C恰好是AB的中点,则DE= cm;若AC=4cm,则DE= cm;
(2)随着C点位置的改变,DE的长是否会改变?如果改变,请说明原因;如果不变,请求出DE的长;
(3)知识迁移:如图②,已知∠AOB=120°,过角的内部任意一点C画射线OC,若OD、OE分别平分∠AOC和∠BOC,试说明∠DOE的度数与射线OC的位置无关.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有A,B两点,AB=18,原点O是线段AB上的一点,OA=2OB.
(1)求出A,B两点所表示的数;
(2)若点C是线段AO上一点,且满足 AC=CO+CB,求C点所表示的数;
(3)若点E以3个单位长度/秒的速度从点A沿数轴向点B方向匀速运动,同时点F以1个单位长度/秒的速度从点B沿数轴向右匀速运动,并设运动时间为t秒,问t为多少时,E、F两点重合.并求出此时数轴上所表示的数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)2020年9月的日历如图1所示,用1×3的长方形框出3个数.如果任意圈出一横行左右相邻的三个数,设最小的数为x,用含x的式子表示这三个数的和为 ;如果任意圈出一竖列上下相邻的三个数,设最小的数为y,用含y的式子表示这三个数的和为
(2)如图2,用一个2×2的正方形框出4个数,是否存在被框住的4个数的和为96?如果存在,请求出这四个数中的最小的数字;如果不存在,请说明理由
(3)如图2,用一个3×3的正方形框出9个数,在框出的9个数中,记前两行共6个数的和为a1,最后一行3个数的和为a2.若|a1﹣a2|=6,请求出正方形框中位于最中心的数字m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如右图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格.

(1)请在图中画出平移后的△ABC
(2)再在图中画出△ABC的高CD
(3)![]() =
=
(4)在右图中能使![]() 的格点P的个数有 个(点P异于A) .
的格点P的个数有 个(点P异于A) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张庄甲、乙两家草莓采摘园的草莓销售价格相同,“春节期间”,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为![]() (千克),在甲园所需总费用为
(千克),在甲园所需总费用为![]() (元),在乙园所需总费用为
(元),在乙园所需总费用为![]() (元),
(元),![]() 、
、![]() 与
与![]() 之间的函数关系如图所示,折线OAB表示
之间的函数关系如图所示,折线OAB表示![]() 与
与![]() 之间的函数关系.
之间的函数关系.

(1)甲采摘园的门票是 元,两个采摘园优惠前的草莓单价是每千克 元;
(2)当![]() >10时,求
>10时,求![]() 与
与![]() 的函数表达式;
的函数表达式;
(3)游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com