
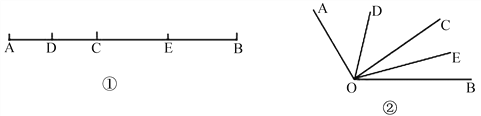
【题目】如图①,已知线段AB=12cm,点C为线段AB上的一个动点,点D、E分别是AC和BC的中点.
(1)若点C恰好是AB的中点,则DE= cm;若AC=4cm,则DE= cm;
(2)随着C点位置的改变,DE的长是否会改变?如果改变,请说明原因;如果不变,请求出DE的长;
(3)知识迁移:如图②,已知∠AOB=120°,过角的内部任意一点C画射线OC,若OD、OE分别平分∠AOC和∠BOC,试说明∠DOE的度数与射线OC的位置无关.
【答案】(1)6,6;(2)DE的长不会改变,理由见解析;(3)理由见解析.
【解析】试题分析:(1)由AB=12cm,点D、E分别是AC和BC的中点,即可推出DE=![]() (AC+BC)=
(AC+BC)= ![]() AB;由AC=4cm,AB=12cm,即可推出BC=8cm,然后根据点D、E分别是AC和BC的中点,即可推出AD=DC,BE=EC,由此即可得到DE的长度;
AB;由AC=4cm,AB=12cm,即可推出BC=8cm,然后根据点D、E分别是AC和BC的中点,即可推出AD=DC,BE=EC,由此即可得到DE的长度;
(2)由(1)知,C点位置的改变后,仍有DE=CD+CE=![]() (AC+BC)=
(AC+BC)= ![]() AB,所以DE的长度不会改变;
AB,所以DE的长度不会改变;
(3)由若OD、OE分别平分∠AOC和∠BOC,即可推出∠DOE=∠DOC+∠COE=![]() (∠AOC+∠COB)=
(∠AOC+∠COB)= ![]() ∠AOB,继而可得到答案.
∠AOB,继而可得到答案.
解:(1)若点C恰好是AB的中点,则DE= 6 cm;
若AC=4cm,则DE= 6 cm;
(2)DE的长不会改变,理由如下:
∵ 点D是线段AC的中点
∴ ![]()
∵ 点E是线段BC的中点
∴ ![]()
∴ DE = DC+CE ![]()
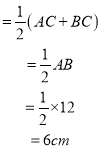
∴ DE的长不会改变;
(3)∵ OD平分∠AOC, OE平分∠BOC
∴![]() ,
, ![]()
∴![]()
![]()
![]()
![]()
![]()
![]()
∴∠DOE的度数与射线OC的位置无关.


科目:初中数学 来源: 题型:
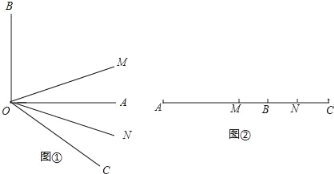
【题目】如图①,∠AOB=90°,∠AOC为∠AOB外的一个角,且∠AOC=30°,射线OM平分∠BOC,ON平分∠AOC.
(1)求∠MON的度数;
(2)如果(1)中∠AOB=α,∠AOC=β.(α,β为锐角),其它条件不变,求出∠MON的度数;
(3)其实线段的计算与角的计算存在着紧密的联系,如图②线段AB=m,延长线段AB到C,使得BC=n,点M,N分别为AC,BC的中点,求MN的长(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强防汛工作,某市对一拦水坝进行加固,如图,加固前拦水坝的横断面是梯形ABCD.已知迎水坡面AB=12米,背水坡面CD=12 ![]() 米,∠B=60°,加固后拦水坝的横断面为梯形ABED,tanE=
米,∠B=60°,加固后拦水坝的横断面为梯形ABED,tanE= ![]() ,则CE的长为米.
,则CE的长为米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在八年级开展环保知识问卷调查活动,问卷一共10道题,八年级(三)班的问卷得分情况统计图如下图所示:

(1)扇形统计图中,a等于多少;
(2)根据以上统计图中的信息,①问卷得分的极差是多少分,②问卷得分的众数是多少分,③问卷得分的中位数是多少分;
(3)请你求出该班同学的平均分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有七个数﹣1,﹣2,﹣2,﹣4,﹣4,﹣8,﹣8将它们填入图1(3个圆两两相交分成7个部分)中,使得每个圆内部的4个数之积相等,设这个积为m,如图2给出了一种填法,此时m=64,在所有的填法中,m的最大值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,点A,B的横坐标分别为a、a+2,二次函数y=﹣x2+(m﹣2)x+2m的图象经过点A,B,且a、m满足2a﹣m=d(d为常数).
(1)若一次函数y1=kx+b的图象经过A、B两点.
①当a=1、d=﹣1时,求k的值;
②若y1随x的增大而减小,求d的取值范围;
(2)当d=﹣4且a≠﹣2、a≠﹣4时,判断直线AB与x轴的位置关系,并说明理由;
(3)点A,B的位置随着a的变化而变化,设点A,B运动的路线与y轴分别相交于点C,D,线段CD的长度会发生变化吗?如果不变,求出CD的长;如果变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列方程:①![]() ;②0.3x=1;③
;②0.3x=1;③![]() ;④x2﹣4x=3;⑤x=6;⑥x+2y=0.其中一元一次方程的个数是( )
;④x2﹣4x=3;⑤x=6;⑥x+2y=0.其中一元一次方程的个数是( )
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AB的中点,点D在线段CB上.
![]()
(1)图中共有 条线段.
(2)图中AD=AC+CD,BC=AB﹣AC,类似地,请你再写出两个有关线段的和与差的关系式:
① ;② .
(3)若AB=8,DB=1.5,求线段CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com