
【题目】某校在八年级开展环保知识问卷调查活动,问卷一共10道题,八年级(三)班的问卷得分情况统计图如下图所示:

(1)扇形统计图中,a等于多少;
(2)根据以上统计图中的信息,①问卷得分的极差是多少分,②问卷得分的众数是多少分,③问卷得分的中位数是多少分;
(3)请你求出该班同学的平均分.
【答案】(1)a=14%;(2)①极差是40(分),②众数是90分,③中位数是85(分);(3)该班同学的平均分为82.6(分).
【解析】
(1)依据扇形统计图中各项目的百分比,即可得到a的值;
(2)依据极差、众数和中位数的定义进行计算,即可得到答案;
(3)依据加权平均数的算法进行计算,即可得到该班同学的平均分.
(1)a=1﹣20%﹣30%﹣20%﹣16%=14%;
故答案为:14%;
(2)①问卷得分的极差是100﹣60=40(分),
②90分所占的比例最大,故问卷得分的众数是90分,
③问卷得分的中位数是![]() =85(分);
=85(分);
故答案为:40;90;85;
(3)该班同学的平均分为:60×14%+70×16%+80×20%+90×30%+100×20%=82.6(分).


 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】(知识生成)
我们已经知道,通过不同的方法表示同一图形的面积,可以探求相应的等式.
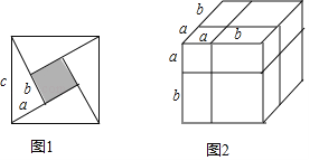
2002年8月在北京召开了国际数学大会,大会会标如图1所示,它是由四个形状大小完全相同的直角三角形与中间的小正方形拼成的一个大正方形,直角三角形的两条直角边长分别为a、b ( a<b ),斜边长为c.
(1)图中阴影部分的面积用两种方法可分别表示为 、 ;
(2)你能得出的a,b,c之间的数量关系是 (等号两边需化为最简形式);
(3)一直角三角形的两条直角边长为6和8,则其斜边长为 .
(知识迁移)
通过不同的方法表示同一几何体的体积,也可以探求相应的等式.如图2是边长为a+b的正方体,被如图所示的分割线分成8块.
(4)用不同方法计算这个正方体体积,就可以得到一个等式,这个等式可以为 .(等号两边需化为最简形式)
(5)已知a+b=3,ab=1,利用上面的规律求a3+b3的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小山岗的斜坡AC的坡角α=45°,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,小山岗的高AB约为(结果取整数,参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50)( )
A.164m
B.178m
C.200m
D.1618m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB>∠ABC.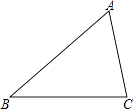
(1)用直尺和圆规在∠ACB的内部作射线CM,使∠ACM=∠ABC(不要求写作法,保留作图痕迹);
(2)若(1)中的射线CM交AB于点D,AB=9,AC=6,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.
(1)求证:△ABE≌△DAF;
(2)若AF=1,四边形ABED的面积为6,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=12cm,C为AB延长线上一点,CP与⊙O相切于点P,过点B作弦BD∥CP,连接PD.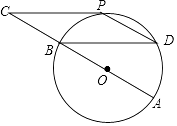
(1)求证:点P为 ![]() 的中点;
的中点;
(2)若∠C=∠D,求四边形BCPD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
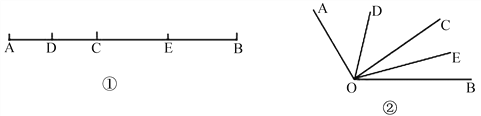
【题目】如图①,已知线段AB=12cm,点C为线段AB上的一个动点,点D、E分别是AC和BC的中点.
(1)若点C恰好是AB的中点,则DE= cm;若AC=4cm,则DE= cm;
(2)随着C点位置的改变,DE的长是否会改变?如果改变,请说明原因;如果不变,请求出DE的长;
(3)知识迁移:如图②,已知∠AOB=120°,过角的内部任意一点C画射线OC,若OD、OE分别平分∠AOC和∠BOC,试说明∠DOE的度数与射线OC的位置无关.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)2020年9月的日历如图1所示,用1×3的长方形框出3个数.如果任意圈出一横行左右相邻的三个数,设最小的数为x,用含x的式子表示这三个数的和为 ;如果任意圈出一竖列上下相邻的三个数,设最小的数为y,用含y的式子表示这三个数的和为
(2)如图2,用一个2×2的正方形框出4个数,是否存在被框住的4个数的和为96?如果存在,请求出这四个数中的最小的数字;如果不存在,请说明理由
(3)如图2,用一个3×3的正方形框出9个数,在框出的9个数中,记前两行共6个数的和为a1,最后一行3个数的和为a2.若|a1﹣a2|=6,请求出正方形框中位于最中心的数字m的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com