【题目】用适当的方法解方程：
（1）（2x﹣5）2﹣9＝0
（2）2x2﹣3x﹣2＝0
（3）x2+2x﹣399＝0
（4）2（x﹣3）＝2x（x﹣3）
【答案】（1）x1＝1，x2＝4；（2）x1＝﹣
，x2＝2；（3）x1＝﹣21，x2＝19；（4）x1＝3，x2＝1．
【解析】
（1）根据因式分解法即可求解；
（2）根据因式分解法即可求解；
（3）根据因式分解法即可求解；
（4）根据因式分解法即可求解.
解：（1）（2x﹣5）2﹣9＝0，
（2x﹣5+3）（2x﹣5﹣3）＝0，
2x﹣5+3＝0，2x﹣5﹣3＝0，
x1＝1，x2＝4；
（2）2x2﹣3x﹣2＝0，
（2x+1）（x﹣2）＝0，
2x+1＝0，x﹣2＝0，
x1＝﹣，x2＝2；
（3）x2+2x﹣399＝0，
（x+21）（x﹣19）＝0，
x+21＝0，x﹣19＝0，
x1＝﹣21，x2＝19；
（4）2（x﹣3）＝2x（x﹣3），
2（x﹣3）﹣2x（x﹣3）＝0，
2（x﹣3）（1﹣x）＝0，
x﹣3＝0，1﹣x＝0，
x1＝3，x2＝1．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】在一次数学课上，张老师出示了一个题目：“如图，ABCD的对角线相交于点O，过点O作EF垂直于BD交AB，CD分别于点F，E，连接DF，
请根据上述条件，写出一个正确结论
”其中四位同学写出的结论如下：
小青：
；小何：四边形DFBE是正方形；
小夏：
；小雨：
．
这四位同学写出的结论中不正确的是
A. 小青 B. 小何 C. 小夏 D. 小雨
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知直线
与抛物线
相交于A，B两点，且点A（1，－4）为抛物线的顶点，点B在x轴上。
（1）求抛物线的解析式；
（2）在（1）中抛物线的第二象限图象上是否存在一点P，使△POB与△POC全等？若存在，求出点P的坐标；若不存在，请说明理由；
（3）若点Q是y轴上一点，且△ABQ为直角三角形，求点Q的坐标。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如果关于x的一元二次方程
有两个实数根，且其中一个根为另一个根的2倍，则称这样的方程为“倍根方程”．以下关于倍根方程的说法，正确的是________．（写出所有正确说法的序号）．
①方程
是倍根方程；
②若
是倍根方程，则
；
③若点
在反比例函数
的图像上，则关于
的方程
是倍根方程；
④若方程
是倍根方程，且相异两点
， 
都在抛物线
上，则方程
的一个根为
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图1，在Rt△ABC 中， 
，D、E是斜边BC上两动点，且∠DAE=45°，将△
绕点
逆时针旋转90后，得到△
，连接
.
（1）试说明：△
≌△
；
（2）当BE=3,CE=9时，求∠BCF的度数和DE的长；
（3）如图2，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，D是斜边BC所在直线上一点，BD=3，BC=8，求DE2的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
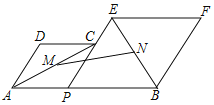
【题目】如图，已知AB=12，P为线段AB上的一个动点，分别以AP、PB为边在AB的同侧作菱形APCD和菱形PBFE，点P、C、E在一条直线上，∠DAP=60°．M、N分别是对角线AC、BE的中点．当点P在线段AB上移动时，点M、N之间的距离最短为______．（结果留根号）
查看答案和解析>>
科目：初中数学 来源： 题型：
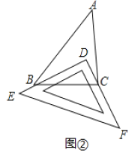
【题目】材料阅读：如图①所示的图形，像我们常见的学习用品—圆规.我们不妨把这样图形叫做“规形图”.
解决问题：
（1）观察“规形图”，试探究
与
，
，
之间的数量关系，并说明理由；
（2）请你直接利用以上结论，解决以下两个问题：
Ⅰ.如图②，把一块三角尺
放置在
上，使三角尺的两条直角边
，
恰好经过点
，
，若
，则
_____
.
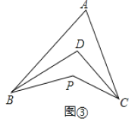
Ⅱ.如图③，
平分
，
平分
，若，
，求的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，直线AB与函数y＝
（x＞0）的图象交于点A（m，2），B（2，n）．过点A作AC平行于x轴交y轴于点C，在y轴负半轴上取一点D，使OD＝
OC，且△ACD的面积是6，连接BC．
（1）求m，k，n的值；
（2）求△ABC的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
