
分析 利用AB=|a-b|,即可求出答案.
解答 解:(1)5-2=3,
-2-(-5)=3,
1-(-3)=4;
(2)∵|a+1|=2,
∴a+1=±2,
∴a=-3或a=1,
∵|a+2|+|a-1|=6,
当a<-2时,
∴-(a+2)-(a-1)=6,
∴a=-$\frac{7}{2}$,
当-2≤a≤1时,
∴a+2-(a-1)=6,
∴3=6,此时矛盾,
当a>1时,
∴a+2+a-1=6,
∴a=$\frac{5}{2}$,
综上所述,a=-$\frac{7}{2}$或a=$\frac{5}{2}$;
(3)当a在数轴上表示-2和1之间时,
此时|a+2|+|a-1|的最小值为3,
此时-2≤a≤1,
(4)由于当-5≤a≤3时,
此时|a+5|+|a-3|最小值为8,
∴若要|a+5|+|a-1|+|a-3|的值最小,
只需要|a-1|的值最小即可,
此时a=1,|a-1|=0,
∴|a+5|+|a-1|+|a-3|最小是为8,
故答案为:(1)3,3,4;
(2)-3或1,-$\frac{7}{2}$或$\frac{5}{2}$;
(3)3,-2≤a≤1;
(4)1,8.
点评 本题考查数轴,涉及绝对值,解方程等知识,综合程度较高.


科目:初中数学 来源: 题型:填空题
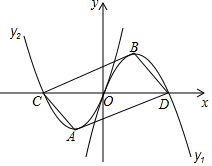 如图,过原点的两条抛物线y1=mx2+nx,(m<0,n>0),y2=-mx2+nx,(m<0,n>0),它们与x轴的另一个交点分别为D、C,顶点分别为B、A,若以点A、B、C、D为顶点的四边形为矩形时,n的值为2$\sqrt{3}$.
如图,过原点的两条抛物线y1=mx2+nx,(m<0,n>0),y2=-mx2+nx,(m<0,n>0),它们与x轴的另一个交点分别为D、C,顶点分别为B、A,若以点A、B、C、D为顶点的四边形为矩形时,n的值为2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 626 | B. | 288 | C. | 168 | D. | 624 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 越来越接近1 | B. | 越来越接近0 | ||
| C. | 没有什么明显的规律 | D. | 越来越大 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
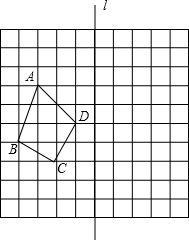 如图,在由边长为1的小正方形组成的10×10的网格中(我们把组成网格的小正方形的顶点称为格点),四边形ABCD在直线l的左侧,其四个顶点A,B,C,D分别在网格的格点上.
如图,在由边长为1的小正方形组成的10×10的网格中(我们把组成网格的小正方形的顶点称为格点),四边形ABCD在直线l的左侧,其四个顶点A,B,C,D分别在网格的格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,AD是△ABC的角平分线,DF⊥AB,垂足为点F,DE=DG.若△ADG和△AED的面积分别为50和30,则△EDF的面积为7.5.
如图,AD是△ABC的角平分线,DF⊥AB,垂足为点F,DE=DG.若△ADG和△AED的面积分别为50和30,则△EDF的面积为7.5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com