
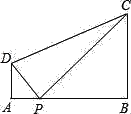
【题目】如图,∠A=∠B=90°,AB=7,AD=2,BC=3,如果边AB上的点P使得以P,A,D为顶点的三角形和以P,B,C为顶点的三角形相似,则这样的P点共有几个( )
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】
根据相似三角形的判定与性质,当若点A,P,D分别与点B,C,P对应,与若点A,P,D分别与点B,P,C对应,分别分析得出AP的长度即可.
若点A,P,D分别与点B,C,P对应,即△APD∽△BCP,
∴![]() ,
,
∴![]() ,
,
∴AP27AP+6=0,
∴AP=1或AP=6,
当AP=1时,由BC=3,AD=2,BP=6,
∴![]() ,
,
又∵∠A=∠B=90°,
∴△APD∽△BCP.
当AP=6时,由BC=3,AD=2,BP=1,
又∵∠A=∠B=90°,
∴△APD∽△BCP.
若点A,P,D分别与点B,P,C对应,即△APD∽△BPC.
∴![]() ,
,
∴![]() ,
,
∴AP=![]() .
.
检验:当AP=![]() 时,∵BP=
时,∵BP=![]() ,AD=2,BC=3,
,AD=2,BC=3,
∴![]() ,
,
又∵∠A=∠B=90°,
∴△APD∽△BPC.
因此,点P的位置有三处,即在线段AP的长为1、![]() 、6,
、6,
故选:C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
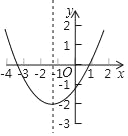
【题目】已知二次函数y=ax2+bx+c(a≠0)图象如图所示,下列结论:
①abc<0;②2a﹣b<0;③a﹣b+c>0;④点(﹣3,y1),(1,y2)都在抛物线上,则有y1>y2.其中正确的结论有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法“①凡正方形都相似;②凡等腰三角形都相似;③凡等腰直角三角形都相似;④直角三角形斜边上的中线与斜边的比为![]() ;⑤两个相似多边形的面积比为
;⑤两个相似多边形的面积比为![]() ,则周长的比为
,则周长的比为![]() .”中,正确的个数有( )个
.”中,正确的个数有( )个
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
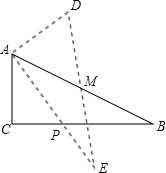
【题目】如图,在△ABC中,∠C=90°,AB=10,cosB=![]() ,点M是AB边的中点,将△ABC绕着点M旋转,使点C与点A重合,点A与点D重合,点B与点E重合,得到△DEA,且AE交CB于点P,那么线段CP的长是__________.
,点M是AB边的中点,将△ABC绕着点M旋转,使点C与点A重合,点A与点D重合,点B与点E重合,得到△DEA,且AE交CB于点P,那么线段CP的长是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
材料![]() .若一元二次方程
.若一元二次方程 ![]() 的两根为
的两根为 ![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
材料![]() .已知实数
.已知实数 ![]() ,
,![]() 满足
满足 ![]() ,
,![]() ,且
,且 ![]() ,求
,求![]() 的值.
的值.
解:由题知 ![]() ,
,![]() 是方程
是方程 ![]() 的两个不相等的实数根,
的两个不相等的实数根,
根据材料 ![]() 得
得 ![]() ,
,![]() ,
,
∴![]() .
.
解决问题:
(1)一元二次方程 ![]() 的两根为
的两根为 ![]() ,
,![]() ,则
,则 ![]() ,
,![]() .
.
(2)已知实数 ![]() ,
,![]() 满足
满足 ![]() ,
,![]() ,且
,且![]() ,求
,求
![]() 的值.
的值.
(3)已知实数 ![]() ,
,![]() 满足
满足 ![]() ,
,![]() ,且
,且 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
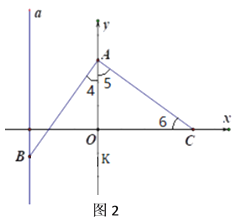
【题目】已知,在平面直角坐标系中,点![]() ,
,![]() ,过
,过![]() 点作直线
点作直线![]() 与
与![]() 轴互相垂直,
轴互相垂直,![]() 为
为![]() 轴上的一个动点,且
轴上的一个动点,且![]() .
.
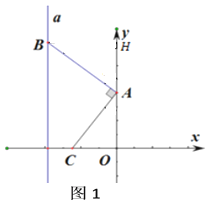
(1)如图1,若点![]() 是第二象限内的一个点,且
是第二象限内的一个点,且![]() 时,求点
时,求点![]() 的坐标;(用
的坐标;(用![]() 的代数式表示)
的代数式表示)
(2)如图2,若点![]() 是第三象限内的一个点,设
是第三象限内的一个点,设![]() 点的坐标
点的坐标![]() ,求
,求![]() 的取值范围:
的取值范围:
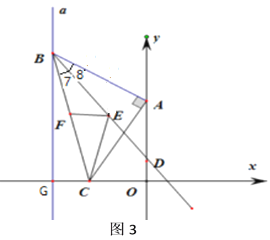
(3)如图3,连接![]() ,作
,作![]() 的平分线
的平分线![]() ,点
,点![]() 、
、![]() 分别是射线
分别是射线![]() 与边
与边![]() 上的两个动点,连接
上的两个动点,连接![]() 、
、![]() ,当
,当![]() 时,试求
时,试求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘渔船正以60海里/小时的速度向正东方向航行,在A处测得岛礁P在东北方向上,继续航行1.5小时后到达B处此时测得岛礁P在北偏东30°方向,同时测得岛礁P正东方向上的避风港M在北偏东60°方向。为了在台风到来之前用最短时间到达M处,渔船立刻加速以75海里/小时的速度继续航行多少小时即可到达? (结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
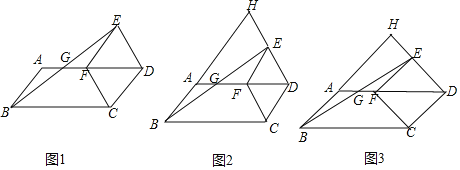
【题目】如图1,以□ABCD的较短边CD为一边作菱形CDEF,使点F落在边AD上,连接BE,交AF于点G.
(1)猜想BG与EG的数量关系.并说明理由;
(2)延长DE,BA交于点H,其他条件不变,
①如图2,若∠ADC=60°,求![]() 的值;
的值;
②如图3,若∠ADC=α(0°<α<90°),直接写出![]() 的值.(用含α的三角函数表示)
的值.(用含α的三角函数表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市对今年“元旦”期间销售A、B、C三种品牌的绿色鸡蛋情况进行了统计,并绘制如图所示的扇形统计图和条形统计图.根据图中信息解答下列问题:
(1)该超市“元旦”期间共销售 个绿色鸡蛋,A品牌绿色鸡蛋在扇形统计图中所对应的扇形圆心角是 度;
(2)补全条形统计图;
(3)如果该超市的另一分店在“元旦”期间共销售这三种品牌的绿色鸡蛋1500个,请你估计这个分店销售的B种品牌的绿色鸡蛋的个数?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com