
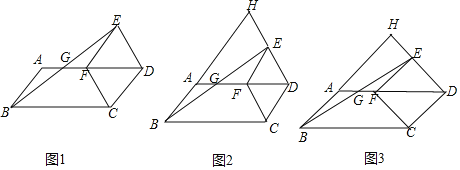
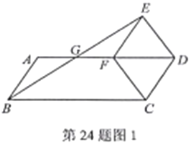
【题目】如图1,以□ABCD的较短边CD为一边作菱形CDEF,使点F落在边AD上,连接BE,交AF于点G.
(1)猜想BG与EG的数量关系.并说明理由;
(2)延长DE,BA交于点H,其他条件不变,
①如图2,若∠ADC=60°,求![]() 的值;
的值;
②如图3,若∠ADC=α(0°<α<90°),直接写出![]() 的值.(用含α的三角函数表示)
的值.(用含α的三角函数表示)
【答案】(1)![]() ,理由见解析;(2)
,理由见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)BG=EG,根据已知条件易证△BAG≌△EFG,根据全等三角形的对应边相等即可得结论;(2)①方法一:过点G作GM∥BH,交DH于点M,证明ΔGME∽ΔBHE,即可得![]() ,再证明
,再证明![]() 是等边三角形,可得
是等边三角形,可得 ![]() ,由此可得
,由此可得![]() ;方法二:延长
;方法二:延长![]() ,
,![]() 交于点
交于点![]() ,证明ΔHBM为等边三角形,再证明
,证明ΔHBM为等边三角形,再证明![]() ∽
∽![]() ,即可得结论;②如图3,连接EC交DF于O根据三角函数定义得cosα=
,即可得结论;②如图3,连接EC交DF于O根据三角函数定义得cosα=![]() ,则OF=bcosα,DG=a+2bcosα,同理表示AH的长,代入
,则OF=bcosα,DG=a+2bcosα,同理表示AH的长,代入![]() 计算即可.
计算即可.
(1)![]() ,
,
理由如下:
∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ∥
∥![]() ,
,![]() .
.
∵四边形![]() 是菱形,
是菱形,
∴![]() ∥
∥![]() ,
,![]() .
.
∴![]() ∥
∥![]() ,
,![]() .
.
∴![]() .
.
又∵![]() ,
,
∴![]() ≌
≌![]()
![]() .
.
∴![]() .
.
(2)方法1:过点![]() 作
作![]() ∥
∥![]() ,交
,交![]() 于点
于点![]() ,
,
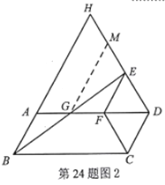
∴![]() .
.
∵![]() ,
,
∴![]() ∽
∽![]() .
.
∴![]() .
.
由(1)结论知![]() .
.
∴![]() .
.
∴![]() .
.
∵四边形![]() 为菱形,
为菱形,
∴![]() .
.
∵四边形![]() 是平行四边形,
是平行四边形,
![]() ∥
∥![]() .
.
∴![]() .
.
∵![]() ∥
∥![]() ,
,
∴![]() .
.
∴![]() ,
,
即![]() .
.
∴![]() 是等边三角形。
是等边三角形。
∴![]() .
.
∴![]() .
.
方法2:延长![]() ,
,![]() 交于点
交于点![]() ,
,
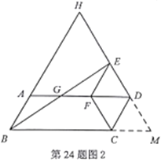
∵四边形![]() 为菱形,
为菱形,
∴![]() .
.
∵四边形![]() 为平形四边形,
为平形四边形,
∴![]() ,
,![]() ∥
∥![]() .
.
∴![]() .
.
![]() ,
,
即![]() .
.
∴![]() 为等边三角形.
为等边三角形.
∴![]() .
.
∵![]() ∥
∥![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ∽
∽![]() ,
,
∴![]() .
.
由(1)结论知![]()
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
(3)![]() . 如图3,连接EC交DF于O,
. 如图3,连接EC交DF于O,
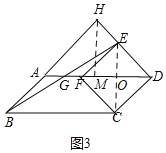
∵四边形CFED是菱形,
∴EC⊥AD,FD=2FO,
设FG=a,AB=b,则FG=a,EF=ED=CD=b,
Rt△EFO中,cosα=![]() ,
,
∴OF=bcosα,
∴DG=a+2bcosα,
过H作HM⊥AD于M,
∵∠ADC=∠HAD=∠ADH=α,
∴AH=HD,
∴AM=![]() AD=
AD=![]() (2a+2bcosα)=a+bcosα,
(2a+2bcosα)=a+bcosα,
Rt△AHM中,cosα=![]() ,
,
∴AH=![]() ,
,
∴![]() =
=![]() =cosα.
=cosα.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B=90°,AB=7,AD=2,BC=3,如果边AB上的点P使得以P,A,D为顶点的三角形和以P,B,C为顶点的三角形相似,则这样的P点共有几个( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD的值最小时,点P的坐标为( )
x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD的值最小时,点P的坐标为( )

A.(﹣1,0)B.(﹣2,0)C.(﹣3,0)D.(﹣4,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是正方形,点E是边BC上的任意一点,AE⊥EF,且直线EF交正方形外角的平分线CF于点F.
(1)如图1,求证:AE=EF;
(2)如图2,当AB=2,点E是边BC的中点时,请直接写出FC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;并写出点A2、B2、C2坐标;
(3)请画出△ABC绕O逆时针旋转90°后的△A3B3C3;并写出点A3、B3、C3坐标.
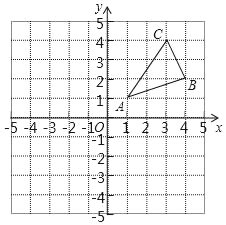
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆高铁与一辆动车组列车在长为1320千米的京沪高速铁路上运行,已知高铁列车比动车组列车平均速度每小时快99千米,且高铁列车比动车组列车全程运行时间少3小时,求这辆高铁列车全程运行的时间和平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 的坐标为
的坐标为![]() ,
,![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 轴,垂足为
轴,垂足为![]() ,点
,点![]() 分别是射线
分别是射线![]() 、
、![]() 上的动点,且点
上的动点,且点![]() 不与点
不与点![]() 、
、![]() 重合,
重合,![]() .
.

(1)如图1,当点![]() 在线段
在线段![]() 上时,求
上时,求![]() 的周长;
的周长;
(2)如图2,当点![]() 在线段
在线段![]() 的延长线上时,设
的延长线上时,设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,请猜想
,请猜想![]() 与
与![]() 之间的等量关系,并证明你的猜想.
之间的等量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )

A. 20° B. 25° C. 30° D. 45°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com