练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】永康市某校在课改中，开设的选修课有：篮球，足球，排球，羽毛球，乒乓球，学生可根据自己的爱好选修一门，李老师对九（1）班全班同学的选课情况进行调查统计，制成了两幅不完整的统计图（如图）．

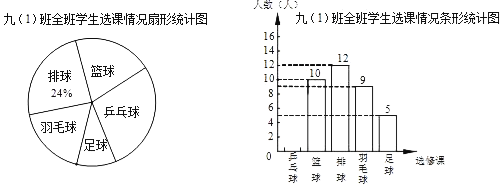
    （1）该班共有学生　 　人，并补全条形统计图；

    （2）求“篮球”所在扇形圆心角的度数；

    （3）九（1）班班委4人中，甲选修篮球，乙和丙选修足球，丁选修排球，从这4人中任选2人，请你用列表或画树状图的方法，求选出的2人中恰好为1人选修篮球，1人选修足球的概率．

    【答案】(1)50,图形见解析；（2）72°；（3）

    【解析】

    （1）用排球的人数除以它所占的百分比即可得到全班人数，用总人数减去其它选课的人数求出乒乓球的人数，从而补全统计图；
    （2）用篮球的所占百分比乘以360°即可得到在扇形统计图中“篮球”对应扇形的圆心角的度数；
    （3）先画树状图展示所有12种等可能的结果数，找出选出的2人恰好1人选修篮球，1人选修足球所占结果数，然后根据概率公式求解．

    （1）该班共有学生（人），

    乒乓球有50﹣10﹣12﹣9﹣5＝14（人），

    补图如下：

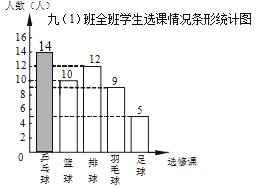
    故答案为：50；

    （2）；

    （3）根据题意画图如下：用A表示篮球，用B表示足球，用C表示排球；

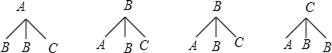
    共有12种等可能的结果数，其中选出的2人恰好1人选修篮球，1人选修足球占4种，

    所以选出的2人恰好1人选修篮球，1人选修足球的概率

    所求的概率为 ．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】2019年3月30日，四川省凉山州木里县境内发生森林火灾，30名左右的扑火英雄牺牲，让人感到痛心，也再次给我们的防火安全意识敲响警钟．为了加强学生的防火安全意识，某校举行了一次“防火安全知识竞赛”（满分100分），赛后从中抽取了部分学生的成绩进行整理，并制作了如下不完整的统计图表：

    组别

    成绩x/分

    组中值

    A

    50≤x＜60

    55

    B

    60≤x＜70

    65

    C

    70≤x＜80

    75

    D

    80≤x＜90

    85

    E

    90≤x＜100

    95

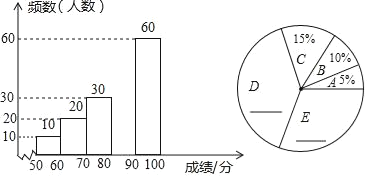
    请根据图表提供的信息，解答下列各题：

    （1）补全频数分布直方图和扇形统计图；

    （2）分数段80≤x＜90对应扇形的圆心角的度数是　 　°，所抽取的学生竞赛成绩的中位数落在　 　区间内；

    （3）若将每组的组中值（各组两个端点的数的平均数）代表各组每位学生的竞赛成绩，请你估计该校参赛学生的平均成绩．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=ax2+bx+c与x轴交于点（-1，0），顶点坐标为（1，m），与y轴交点在（0，3），（0，4）之（不包含端点），现有下列结论：①3a+b＞0；②-＜a＜-1；③关于x的方程ax2+bx+c=m-2有两个不相等的实数根：④若点M（-1.5，y1），N（2.5，y2）是函数图象上的两点，则y1=y2．其中正确结论的个数为（　　）

    A.1B.2C.3D.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD边长为4，点O在对角线DB上运动（不与点B，D重合），连接OA，作OP⊥OA，交直线BC于点P．

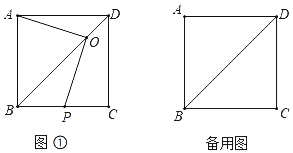
    （1）判断线段OA，OP的数量关系，并说明理由．

    （2）当OD＝时，求CP的长．

    （3）设线段DO，OP，PC，CD围成的图形面积为S1，△AOD的面积为S2，求S1﹣S2的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

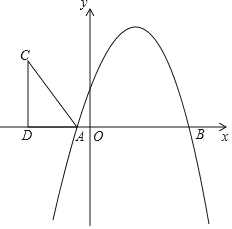
    【题目】如图，抛物线y＝﹣x2+bx+c与x轴分别交于A（﹣1，0），B（5，0）两点．

    （1）求抛物线的解析式；

    （2）在第二象限内取一点C，作CD垂直x轴于点D，连接AC，且AD＝5，CD＝8，将Rt△ACD沿x轴向右平移m个单位，当点C落在抛物线上时，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知CB＝CA，∠ACB＝90°，点D在边BC上（与B，C不重合），四边形ADEF为正方形，过点F作FG⊥CA，交CA的延长线于点G，连接FB，交DE于点Q，得出以下结论：①AC＝FG；②S△FAB：S四边形CBFG＝1：2；③∠ABC＝∠ABF；④AD2＝FQAC．其中正确结论的个数是（　　）

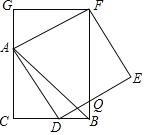
    A. 1B. 2C. 3D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）问题发现

    如图1，在△OAB和△OCD中，OA=OB，OC=OD，∠AOB=∠COD=40°，连接AC，BD交于点M．填空：

    ①的值为　 　；

    ②∠AMB的度数为　 　．

    （2）类比探究

    如图2，在△OAB和△OCD中，∠AOB=∠COD=90°，∠OAB=∠OCD=30°，连接AC交BD的延长线于点M．请判断的值及∠AMB的度数，并说明理由；

    （3）拓展延伸

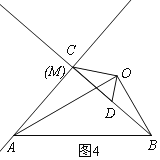
    在（2）的条件下，将△OCD绕点O在平面内旋转，AC，BD所在直线交于点M，若OD=1，OB=，请直接写出当点C与点M重合时AC的长．

    【答案】（1）①1；②40°；（2），90°；（3）AC的长为3或2．

    【解析】

    （1）①证明△COA≌△DOB（SAS），得AC=BD，比值为1；

    ②由△COA≌△DOB，得∠CAO=∠DBO，根据三角形的内角和定理得：∠AMB=180°-（∠DBO+∠OAB+∠ABD）=180°-140°=40°；

    （2）根据两边的比相等且夹角相等可得△AOC∽△BOD，则，由全等三角形的性质得∠AMB的度数；

    （3）正确画图形，当点C与点M重合时，有两种情况：如图3和4，同理可得：△AOC∽△BOD，则∠AMB=90°，，可得AC的长．

    （1）问题发现：

    ①如图1，

    ∵∠AOB=∠COD=40°，

    ∴∠COA=∠DOB，

    ∵OC=OD，OA=OB，

    ∴△COA≌△DOB（SAS），

    ∴AC=BD，

    ∴

    ②∵△COA≌△DOB，

    ∴∠CAO=∠DBO，

    ∵∠AOB=40°，

    ∴∠OAB+∠ABO=140°，

    在△AMB中，∠AMB=180°-（∠CAO+∠OAB+∠ABD）=180°-（∠DBO+∠OAB+∠ABD）=180°-140°=40°，

    （2）类比探究：

    如图2，，∠AMB=90°，理由是：

    Rt△COD中，∠DCO=30°，∠DOC=90°，

    ∴，

    同理得：，

    ∴，

    ∵∠AOB=∠COD=90°，

    ∴∠AOC=∠BOD，

    ∴△AOC∽△BOD，

    ∴ ，∠CAO=∠DBO，

    在△AMB中，∠AMB=180°-（∠MAB+∠ABM）=180°-（∠OAB+∠ABM+∠DBO）=90°；

    （3）拓展延伸：

    ①点C与点M重合时，如图3，

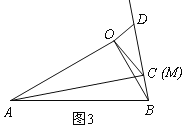
    同理得：△AOC∽△BOD，

    ∴∠AMB=90°，，

    设BD=x，则AC=x，

    Rt△COD中，∠OCD=30°，OD=1，

    ∴CD=2，BC=x-2，

    Rt△AOB中，∠OAB=30°，OB=，

    ∴AB=2OB=2，

    在Rt△AMB中，由勾股定理得：AC2+BC2=AB2，

    (x)2+(x2)2＝(2)2，

    x2-x-6=0，

    （x-3）（x+2）=0，

    x1=3，x2=-2，

    ∴AC=3；

    ②点C与点M重合时，如图4，

    同理得：∠AMB=90°，，

    设BD=x，则AC=x，

    在Rt△AMB中，由勾股定理得：AC2+BC2=AB2，

    (x)2+（x+2）2=(2)2.

    x2+x-6=0，

    （x+3）（x-2）=0，

    x1=-3，x2=2，

    ∴AC=2；.

    综上所述，AC的长为3或2．

    点睛：本题是三角形的综合题，主要考查了三角形全等和相似的性质和判定，几何变换问题，解题的关键是能得出：△AOC∽△BOD，根据相似三角形的性质，并运用类比的思想解决问题，本题是一道比较好的题目．

    【题型】解答题
    【结束】
    25

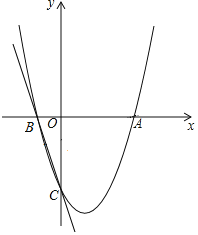
    【题目】如图，已知抛物线y＝ax2+bx﹣3（a≠0）经过点A（3，0），B（﹣1，0）．

    （1）求该抛物线的解析式；

    （2）若以点A为圆心的圆与直线BC相切于点M，求切点M的坐标；

    （3）若点Q在x轴上，点P在抛物线上，是否存在以点B，C，Q，P为顶点的四边形是平行四边形？若存在，直接写出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

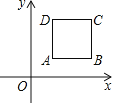
    【题目】如图，正方形ABCD的顶点A（1，1），B（3，1），规定把正方形ABCD“先沿x轴翻折，再向左平移1个单位”为一次变换，这样连续经过2019次变换后，正方形ABCD的顶点C的坐标为（　　）

    A. （﹣2018，3）B. （﹣2018，﹣3）

    C. （﹣2016，3）D. （﹣2016，﹣3）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

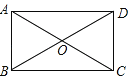
    【题目】已知：如图，矩形ABCD，AB＝2，BC＝4，对角线AC，BD相交于点O，点P在对角线BD上，并且A，O，P组成以OP为腰的等腰三角形，那么OP的长等于___．

    查看答案和解析>>

    同步练习册答案