
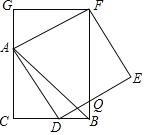
【题目】如图,已知CB=CA,∠ACB=90°,点D在边BC上(与B,C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,得出以下结论:①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQAC.其中正确结论的个数是( )
A. 1B. 2C. 3D. 4
【答案】D
【解析】
由正方形的性质得出∠FAD=90°,AD=AF=EF,证出∠CAD=∠AFG,由AAS证明△FGA≌△ACD,得出AC=FG,①正确;
证明四边形CBFG是矩形,得出S△FAB=![]() FB
FB![]() FG=
FG=![]() S四边形CBFG,②正确;
S四边形CBFG,②正确;
由等腰直角三角形的性质和矩形的性质得出∠ABC=∠ABF=45°,③正确;
证出△ACD∽△FEQ,得出对应边成比例,得出AD![]() FE=AD
FE=AD![]() =FQ
=FQ![]() AC,④正确
AC,④正确
解:∵四边形ADEF为正方形,
∴∠FAD=90°,AD=AF=EF,
∴∠CAD+∠FAG=90°,
∵FG⊥CA,
∴∠GAF+∠AFG=90°,
∴∠CAD=∠AFG,
在△FGA和△ACD中,
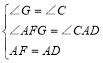 ,
,
∴△FGA≌△ACD(AAS),
∴AC=FG,故①正确;
∵BC=AC,
∴FG=BC,
∵∠ACB=90°,FG⊥CA,
∴FG∥BC,
∴四边形CBFG是矩形,
∴∠CBF=90°,S△FAB=![]() FBFG=
FBFG=![]() S四边形CBFG,故②正确;
S四边形CBFG,故②正确;
∵CA=CB,∠C=∠CBF=90°,
∴∠ABC=∠ABF=45°,故③正确;
∵∠FQE=∠DQB=∠ADC,∠E=∠C=90°,
∴△ACD∽△FEQ,
∴AC:AD=FE:FQ,
∴ADFE=AD2=FQAC,故④正确;
故选:D.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】问题提出:
(1)如图①,已知线段AB和BC,AB=2,BC=5,则线段AC的最小值为 ;
问题探究
(2)如图②,已知扇形COD中,∠COD=90°,DO=CO=6,点A是OC的中点,延长OC到点F,使CF=OC,点P是![]() 上的动点,点B是OD上的一点,BD=1.
上的动点,点B是OD上的一点,BD=1.
(i)求证:△OAP~△OPF;
(ii)求BP+2AP的最小值;
问题解决:
(3)如图③,有一个形状为四边形ABCD的人工湖,BC=9千米,CD=4![]() 千米,∠BCD=150°,现计划在湖中选取一处建造一座假山P,且BP=3千米,为方便游客观光,从C、D分别建小桥PD,PC.已知建桥PD每千米的造价是3万元,建桥PC每千米的造价是1万元,建桥PD和PC的总造价是否存在最小值?若存在,请确定点P的位置并求出总造价的最小值,若不存在,请说明理由.(桥的宽度忽略不计)
千米,∠BCD=150°,现计划在湖中选取一处建造一座假山P,且BP=3千米,为方便游客观光,从C、D分别建小桥PD,PC.已知建桥PD每千米的造价是3万元,建桥PC每千米的造价是1万元,建桥PD和PC的总造价是否存在最小值?若存在,请确定点P的位置并求出总造价的最小值,若不存在,请说明理由.(桥的宽度忽略不计)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有边长为a的正方形卡片①,边长为b的正方形卡片②,两邻边长分别为a,b的矩形卡片③若干张.
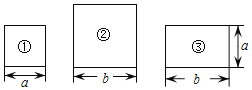
(1)请用2张卡片①,1张卡片②,3张卡片③拼成一个矩形,在方框中画出这个矩形的草图;
(2)请结合拼图前后面积之间的关系写出一个等式;
(3)小明想用类似方法解释多项式乘法(a+3b)(2a+2b)的结果,那么需用卡片①______张,卡片②______张,卡片③______张.
查看答案和解析>>
科目:初中数学 来源: 题型:
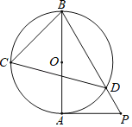
【题目】如图AB是⊙O的直径,PA与⊙O相切于点A,BP与⊙O相交于点D,C为⊙O上的一点,分别连接CB、CD,∠BCD=60°.
(1)求∠ABD的度数;
(2)若AB=6,求PD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】永康市某校在课改中,开设的选修课有:篮球,足球,排球,羽毛球,乒乓球,学生可根据自己的爱好选修一门,李老师对九(1)班全班同学的选课情况进行调查统计,制成了两幅不完整的统计图(如图).
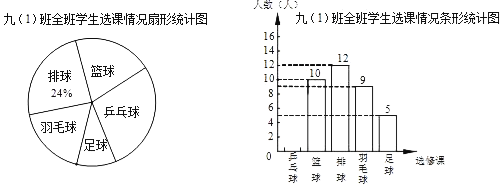
(1)该班共有学生 人,并补全条形统计图;
(2)求“篮球”所在扇形圆心角的度数;
(3)九(1)班班委4人中,甲选修篮球,乙和丙选修足球,丁选修排球,从这4人中任选2人,请你用列表或画树状图的方法,求选出的2人中恰好为1人选修篮球,1人选修足球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣.已知购买甲型机器人1台,乙型机器人2台,共需14万元;购买甲型机器人2台,乙型机器人3台,共需24万元.
(1)求甲、乙两种型号的机器人每台的价格各是多少万元;
(2)已知甲型和乙型机器人每台每小时分拣快递分别是1200件和1000件,该公司计划购买这两种型号的机器人共8台,总费用不超过41万元,并且使这8台机器人每小时分拣快递件数总和不少于8300件,则该公司有哪几种购买方案?哪个方案费用最低,最低费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PQMN的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ.过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=![]() DQ,求点F的坐标.
DQ,求点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
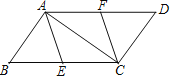
【题目】已知点E、F分别是ABCD的边BC、AD的中点.
(1)求证:四边形AECF是平行四边形;
(2)若BC=10,∠BAC=90°,求AECF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
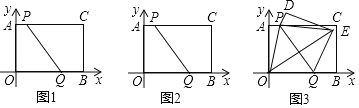
【题目】已知:如图,在平面直角坐标系中,矩形AOBC的顶点C的坐标是(6,4),动点P从点A出发,以每秒1个单位的速度沿线段AC运动,同时动点Q从点B出发,以每秒2个单位的速度沿线段BO运动,当Q到达O点时,P,Q同时停止运动,运动时间是t秒(t>0).
(1)如图1,当时间t= 秒时,四边形APQO是矩形;
(2)如图2,在P,Q运动过程中,当PQ=5时,时间t等于 秒;
(3)如图3,当P,Q运动到图中位置时,将矩形沿PQ折叠,点A,O的对应点分别是D,E,连接OP,OE,此时∠POE=45°,连接PE,求直线OE的函数表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com