
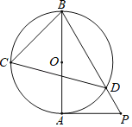
【题目】如图AB是⊙O的直径,PA与⊙O相切于点A,BP与⊙O相交于点D,C为⊙O上的一点,分别连接CB、CD,∠BCD=60°.
(1)求∠ABD的度数;
(2)若AB=6,求PD的长度.
【答案】(1)∠ABD=30°;(2)PD=![]() .
.
【解析】
(1)根据圆周角定理得:∠ADB=90°,由同弧所对的圆周角相等和直角三角形的性质可得结论;
(2)如图1,根据切线的性质可得∠BAP=90°,根据直角三角形30°角的性质可计算AD的长,由勾股定理计算DB的长,由三角函数可得PB的长,从而得PD的长.
(1)如图,连接AD.
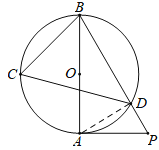
∵BA是⊙O直径,
∴∠BDA=90°.
∵![]() ,
,
∴∠BAD=∠C=60°.
∴∠ABD=90°-∠BAD=90°-60°=30°.
(2)如图,∵AP是⊙O的切线,
∴∠BAP=90°.
在Rt△BAD中,∵∠ABD=30°,
∴DA=![]() BA=
BA=![]() ×6=3.
×6=3.
∴BD=![]() DA=3
DA=3![]() .
.
在Rt△BAP中,∵cos∠ABD=![]() ,
,
∴cos30°=![]() .
.
∴BP=4![]() .
.
∴PD=BP-BD=4![]() -3
-3![]() =
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达![]() 处时,测得小岛
处时,测得小岛![]() 位于它的北偏东
位于它的北偏东![]() 方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛
方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛![]() 位于它的北偏东
位于它的北偏东![]() 方向.如果航母继续航行至小岛
方向.如果航母继续航行至小岛![]() 的正南方向的
的正南方向的![]() 处,求还需航行的距离
处,求还需航行的距离![]() 的长.
的长.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
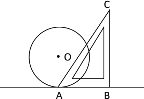
【题目】如图,半径为2的圆O与含30°角的直角三角板ABC的AB边切于点A,将直角三角板沿BA边所在的直线向右平移,当平移到AC与圆O相切时,该直角三角板的平移距离为( )
A. ![]() B.
B. ![]() C. 1D. 2
C. 1D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
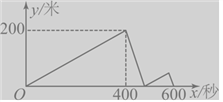
【题目】甲、乙两人在同一直线噵路上同起点,同方向同进出发,分别以不同的速度匀速跑步1500米,当甲超出乙200米时,甲停下来等候乙,甲、乙会合后,两人分别以原来的速度继续跑向终点,先到达终点的人在终点休息,在跑步的整个过程中,甲、乙两人的距离y(米)与出发的时间x(秒)之间的关系如图所示,则甲到终点时,乙距离终点______________米。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD边长为4,点O在对角线DB上运动(不与点B,D重合),连接OA,作OP⊥OA,交直线BC于点P.
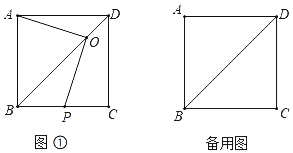
(1)判断线段OA,OP的数量关系,并说明理由.
(2)当OD=![]() 时,求CP的长.
时,求CP的长.
(3)设线段DO,OP,PC,CD围成的图形面积为S1,△AOD的面积为S2,求S1﹣S2的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
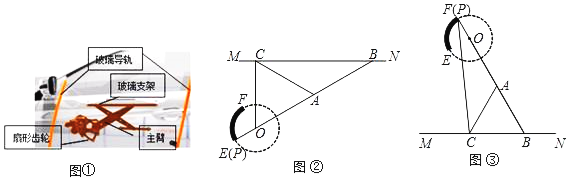
【题目】我们常见的汽车玻璃升降器如图①所示,图②和图③是升降器的示意图,其原理可以看作是主臂PB绕固定的点O旋转,当端点P在固定的扇形齿轮![]() 上运动时,通过叉臂式结构(点B可在MN上滑动)的玻璃支架MN带动玻璃沿导轨作上下运动而达到玻璃升降目的.点O和点P,A,B在同一直线上.当点P与点E重合时,窗户完全闭合(图②),此时∠ABC=30°;当点P与点F重合时,窗户完全打开(图③).已知
上运动时,通过叉臂式结构(点B可在MN上滑动)的玻璃支架MN带动玻璃沿导轨作上下运动而达到玻璃升降目的.点O和点P,A,B在同一直线上.当点P与点E重合时,窗户完全闭合(图②),此时∠ABC=30°;当点P与点F重合时,窗户完全打开(图③).已知![]() 的半径OP=5cm,
的半径OP=5cm,![]() =
=![]() cm,OA=AB=AC=20cm.
cm,OA=AB=AC=20cm.
(1)当窗户完全闭合时,OC=_____cm.
(2)当窗户完全打开时,PC=_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知CB=CA,∠ACB=90°,点D在边BC上(与B,C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,得出以下结论:①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQAC.其中正确结论的个数是( )
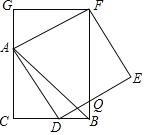
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
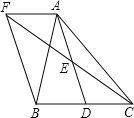
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:BD=CD;
(2)不在原图添加字母和线段,对△ABC只加一个条件使得四边形AFBD是菱形,写出添加条件并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
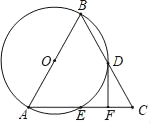
【题目】如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为2,CF=1,求![]() 的长(结果保留π).
的长(结果保留π).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com