
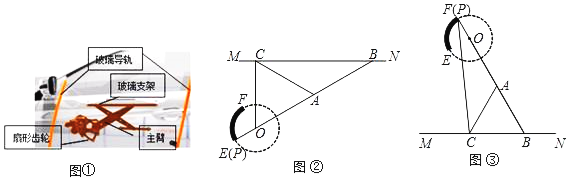
����Ŀ�����dz���������������������ͼ����ʾ��ͼ�ں�ͼ������������ʾ��ͼ����ԭ�����Կ���������PB�ƹ̶��ĵ�O��ת�����˵�P�ڹ̶������γ���![]() ���˶�ʱ��ͨ�����ʽ�ṹ����B����MN�ϻ������IJ���֧��MN���������ص����������˶����ﵽ��������Ŀ�ģ���O�͵�P��A��B��ͬһֱ���ϣ�����P���E�غ�ʱ��������ȫ�պϣ�ͼ�ڣ�����ʱ��ABC��30��������P���F�غ�ʱ��������ȫ��ͼ�ۣ�����֪
���˶�ʱ��ͨ�����ʽ�ṹ����B����MN�ϻ������IJ���֧��MN���������ص����������˶����ﵽ��������Ŀ�ģ���O�͵�P��A��B��ͬһֱ���ϣ�����P���E�غ�ʱ��������ȫ�պϣ�ͼ�ڣ�����ʱ��ABC��30��������P���F�غ�ʱ��������ȫ��ͼ�ۣ�����֪![]() �İ뾶OP��5cm��
�İ뾶OP��5cm��![]() ��
��![]() cm��OA��AB��AC��20cm��
cm��OA��AB��AC��20cm��
��1����������ȫ�պ�ʱ��OC��_____cm��
��2����������ȫ��ʱ��PC��_____cm��
���𰸡�20 5![]()
��������
��1��֤����OCB=90������AOC�ǵȱ������Σ��ɵȱ������ε����ʵó�OC=OA=20cm���ɣ�
��2������PC��OE����PG��MN��G����ͼ��ʾ���ɻ�����ʽ�����EOP=90������������ȫ��ʱ����POC=150�����ó���COE=150��-90��=60������BOC=30������ABC=60�����ó���ABC�ǵȱ������Σ�BC=OA=20�����BP=AB+OA+OP=45��![]() ,
, ![]() ���ó�CG=BG-BC=
���ó�CG=BG-BC=![]() ���ɹ��ɶ������ɵó������
���ɹ��ɶ������ɵó������
�⣺��1����OA��AB��AC��20cm��
���OCB��90����
�ߡ�ABC��30����
���BOC��60����
���AOC�ǵȱ������Σ�
��OC��OA��20cm��
�ʴ�Ϊ20��
��2������PC��OE����PG��MN��G����ͼ����ʾ��

��OCB����PGC��90����
��FG��OC��
���EOP��n����
��![]() �ij���
�ij���![]() ��
��
��ã�n��90��
���EOP��90����
�ɣ�1���ã���������ȫ�պ�ʱ����POC��180����60����150����
���COE��150����90����60����
���BOC��90����60����30����
���ABC��60����
���ABC�ǵȱ������Σ�BC��OA��20��
��BP��AB+OA+OP��45��
![]()
��CG��BG��BC��![]() ��
��
��Rt��PCG�У��ɹ��ɶ����ã�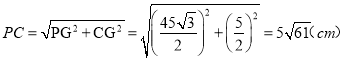 ��
��
�ʴ�Ϊ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ǹ涨���������ߵĶ������������ϣ���Ƹ�������Ϊ�����ắ��������������y��x2��y����x��1��2���������ắ������
��1��������y��x2��4x��4��������y��x2��6x�������ắ������?��˵�����ɣ�
��2����������y��2x2��4mx��m2��16�������ắ��������������ߵı���ʽ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ��ֱ��
��ֱ��![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() ����ֱ��
����ֱ��![]() ��
��![]() ��
��
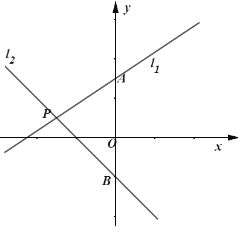
��1����ֱ��![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��2��������![]() ��
��![]() ��Ĵ�����ֱ��
��Ĵ�����ֱ��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ���㣬��
���㣬��![]() ��
��
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
����![]() ��ֱ��д��
��ֱ��д��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���![]() �У�
��![]() ��
��![]() ���Խ���
���Խ���![]() ����
����![]() ��
��![]() ���ϣ�
���ϣ�![]() ��
��![]() ��ƽ�У���
��ƽ�У���![]() ��
��![]() ���ϣ�
���ϣ�
��1����![]() �Ķ�����
�Ķ�����
��2����![]() �ڶԽ���
�ڶԽ���![]() �ϣ���
�ϣ���![]() ���ı���
���ı���![]() �����ڵ�
�����ڵ�![]() ���ұߣ�����
���ұߣ�����![]() ����֪
����֪![]() ��
��![]() ����
����![]() ��
��
����![]() �ij����ú�
�ij����ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
����ijһ����������ͼ��ͬʱ������![]() ��
��![]() ����
����![]() ��ֵ��
��ֵ��
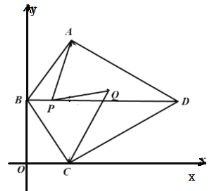
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽����꼶ѧ��������������������꼶���������ȡ�˲���ѧ�����������Գɼ�����![]() �ĸ��ȼ�����ͳ��(˵����
�ĸ��ȼ�����ͳ��(˵����![]() ����90�֡�100�֣�
����90�֡�100�֣�![]() ����75�֡�89�֣�
����75�֡�89�֣�![]() ����60�֡�74�֣�
����60�֡�74�֣�![]() ����60������)������ͳ�ƽ�����Ƴ�������������ͳ��ͼ��������ͳ��ͼ��������Ϣ����������⣺
����60������)������ͳ�ƽ�����Ƴ�������������ͳ��ͼ��������ͳ��ͼ��������Ϣ����������⣺
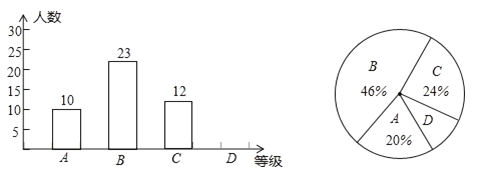
��1��ѧУ�����꼶������������________��ѧ����
��2��������ͳ��ͼ�У�![]() �����ڵ�����Բ�ĽǵĶ�����_________��
�����ڵ�����Բ�ĽǵĶ�����_________��
��3���������ͳ��ͼ����������
��4������У���꼶��500��ѧ���������ͳ�ƽ������ȫУ���꼶����������![]() ��ѧ��Լ�ж�������
��ѧ��Լ�ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
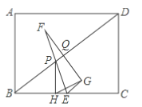
����Ŀ����ͼ���ھ���![]() �У�
��![]() ����
����![]() ��
��![]() ���е㣬��
���е㣬��![]() Ϊ�Խ���
Ϊ�Խ���![]() �ϵĶ��㣬��
�ϵĶ��㣬��![]() ����
����![]() �ڵ�
�ڵ�![]() ������
������![]() ���ӳ�����
���ӳ�����![]() ��ʹ��
��ʹ��![]() ������
������![]() ����
����![]() �ĶԳƵ�
�ĶԳƵ�![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��
��1����֤��![]() ��
��
��2������![]() �˶����Խ���
�˶����Խ���![]() ���е�ʱ����
���е�ʱ����![]() ���ܳ���
���ܳ���
��3���ڵ�![]() ���˶��Ĺ����У�
���˶��Ĺ����У�![]() �Ƿ����Ϊ���������Σ������ԣ����
�Ƿ����Ϊ���������Σ������ԣ����![]() ��ֵ���������ԣ�˵�����ɣ�
��ֵ���������ԣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˵���ѧ�����������༰Ͷ��֪ʶ���˽�������Ӽס�����У�������ȡ40��ѧ�����������֪ʶ���ԣ���������ǵijɼ����ٷ��ƣ����������ݣ��ɼ��������������������ͷ�������������˲�����Ϣ��
a���ס�����У40��ѧ���ɼ���Ƶ���ֲ�ͳ�Ʊ����£�
�ɼ�x ѧУ |
|
|
|
|
|
�� | 4 | 11 | 13 | 10 | 2 |
�� | 6 | 3 | 15 | 14 | 2 |
��˵�����ɼ�80�ּ�����Ϊ���㣬70~79��Ϊ���ã�60~69��Ϊ�ϸ�60������Ϊ���ϸ�
b����У�ɼ���![]() ��һ����ǣ�
��һ����ǣ�
70 70 70 71 72 73 73 73 74 75 76 77 78
c���ס�����У�ɼ���ƽ���֡���λ�����������£�
ѧУ | ƽ���� | ��λ�� | ���� |
�� | 74.2 | n | 5 |
�� | 73.5 | 76 | 84 |
����������Ϣ���ش��������⣺
��1��д������n��ֵ��
��2���ڴ˴β����У�ijѧ���ijɼ���74�֣���������ѧУ����ǰ20�����ɱ������ݿ�֪��ѧ����_____________У��ѧ������������������������������__________��
��3��������У800��ѧ�����μӴ˴β��ԣ����Ƴɼ������ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
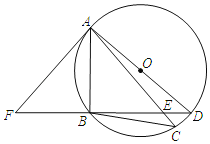
����Ŀ����ͼ��AD����O��ֱ������BA����BC��BD��AC�ڵ�E����F��DB���ӳ����ϣ��ҡ�BAF����C��
��1����֤��AF����O�����ߣ�
��2����֤����ABE�ס�DBA��
��3����BD��8��BE��6����AB�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ�С����һ�λ�У���һ����ѧ����������̽����
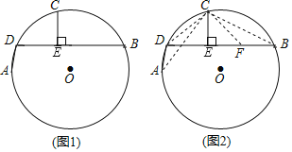
�����ⷢ�֣���ͼ1��AD��BDΪ��O�������ң�AD��BD������CΪ![]() ���е㣬��C��CE��BD������ΪE����֤��BE��DE+AD��
���е㣬��C��CE��BD������ΪE����֤��BE��DE+AD��
������̽����С��ͬѧ��˼·�ǣ���ͼ2����BE�Ͻ�ȡBF��AD������CA��CB��CD��CF���������㰴��С����˼·������������֤�����̣�
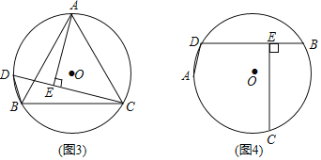
���������ã���ͼ3����ABC�ǡ�O���ڽӵȱ������Σ���D��![]() ��һ�㣬��ACD��45��������BD��CD������A��AE��CD������ΪE����AB��
��һ�㣬��ACD��45��������BD��CD������A��AE��CD������ΪE����AB��![]() ������BCD���ܳ�Ϊ�� ����
������BCD���ܳ�Ϊ�� ����
����ʽ̽������ͼ4�����������ⷢ�֣��С���CΪ![]() ���е㡱��Ϊ����CΪ�Ż�
���е㡱��Ϊ����CΪ�Ż�![]() ���е㡱�������������䣬�������ۡ�BE��DE+AD��������������������˵�����ɣ�������������д��BE��AD��DE֮����µ�����ϵ��������֤����
���е㡱�������������䣬�������ۡ�BE��DE+AD��������������������˵�����ɣ�������������д��BE��AD��DE֮����µ�����ϵ��������֤����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com