
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,对角线
,对角线![]() ,点
,点![]() 在
在![]() 轴上,
轴上,![]() 与
与![]() 轴平行,点
轴平行,点![]() 在
在![]() 轴上.
轴上.
(1)求![]() 的度数.
的度数.
(2)点![]() 在对角线
在对角线![]() 上,点
上,点![]() 在四边形
在四边形![]() 内且在点
内且在点![]() 的右边,连接
的右边,连接![]() ,已知
,已知![]() ,
,![]() ,设
,设![]() .
.
①求![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
②若某一反比例函数图象同时经过点![]() 、
、![]() ,求
,求![]() 的值.
的值.
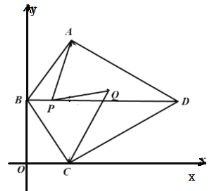
【答案】(1)60°;(2)①![]() ;②
;②![]()
【解析】
(1)连接AC,首先证明![]() ,则有
,则有![]() ,进而可得
,进而可得![]() ,再利用勾股定理即可求出BE,DE的长度,然后利用特殊角的三角函数值即可求出
,再利用勾股定理即可求出BE,DE的长度,然后利用特殊角的三角函数值即可求出![]() 的度数,最后利用
的度数,最后利用![]() 即可求解;
即可求解;
(2)连接AQ,取AD的中点F,连接QF,易证![]() 均为等边三角形,然后证明
均为等边三角形,然后证明![]() ,则有
,则有![]() ,再证明C,Q,F三点共线,然后求出CF的长度,最后利用
,再证明C,Q,F三点共线,然后求出CF的长度,最后利用![]() 即可求解;
即可求解;
(3)先利用平行线分线段成比例求出Q的坐标,然后求出点A的坐标,进而求出反比例函数的解析式,将Q的坐标代入反比例函数解析式中即可求出m的值.
(1)连接AC交BD于点E,
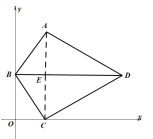
在![]() 和
和![]() 中,
中,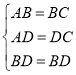
![]()
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
设![]() ,
,
则有![]() ,
,
解得![]() .
.
在![]() 中,
中,
![]() ,
,
![]() ,
,
![]() .
.
(2)①连接AQ,取AD的中点F,连接QF,
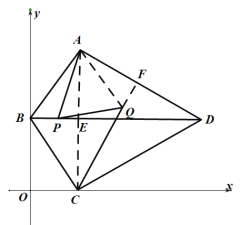
∵![]() ,
,![]() ,
,
![]() 为等边三角形,
为等边三角形,
![]() .
.
∵![]() ,
,![]() ,
,
![]() 为等边三角形,
为等边三角形,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,点F是 AD中点,
,点F是 AD中点,
![]() .
.
在![]() 和
和![]() 中,
中,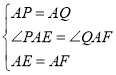
![]()
![]() ,
,
![]() .
.
∵![]() 为等边三角形,点F为AD中点,
为等边三角形,点F为AD中点,
![]() ,
,
∴C,Q,F三点共线.
∵![]() ,
,![]() ,
,
![]() ,
,
![]() ;
;
②过点Q作![]() 交AC于点G,过点F作
交AC于点G,过点F作![]() 交AC于点H,
交AC于点H,
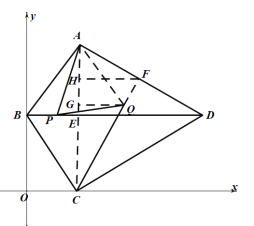
∵![]() ,
,
![]() .
.
∵点F是AD中点,
![]() ,
,
![]() .
.
∵![]() ,
,
![]() ,
,
![]() ,
,
即![]() ,
,
解得![]() ,
,
![]() ,
,
∴点Q的坐标为![]() .
.
![]() ,
,
∴点A的坐标为![]() ,
,
设反比例函数的解析式为![]() ,
,
将点A代入反比例函数中,得![]() ,
,
∴反比例函数的解析式为![]() .
.
将点Q的坐标代入反比例函数的解析式![]() 中,有
中,有
![]() ,
,
解得![]() 或
或![]() (舍去).
(舍去).


科目:初中数学 来源: 题型:
【题目】某校组织数学兴趣探究活动,爱思考的小实同学在探究两条直线的位置关系查阅资料时发现,两条中线互相垂直的三角形称为“中垂三角形”.如图1、图2、图3中,AF、BE是△ABC的中线,AF⊥BE于点P,像△ABC这样的三角形均称为“中垂三角形”.
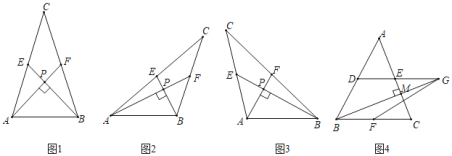
(1)如图1,当∠PAB=45°,AB=6![]() 时,AC= ,BC= ;如图2,当sin∠PAB=
时,AC= ,BC= ;如图2,当sin∠PAB=![]() ,AB=4时,AC= ,BC= ;
,AB=4时,AC= ,BC= ;
(2)请你观察(1)中的计算结果,猜想AB2、BC2、AC2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
(3)如图4,在△ABC中,AB=4![]() ,BC=2
,BC=2![]() ,D、E、F分别是边AB、AC、BC的中点,连结DE并延长至G,使得GE=DE,连结BG,当BG⊥AC于点M时,求GF的长.
,D、E、F分别是边AB、AC、BC的中点,连结DE并延长至G,使得GE=DE,连结BG,当BG⊥AC于点M时,求GF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
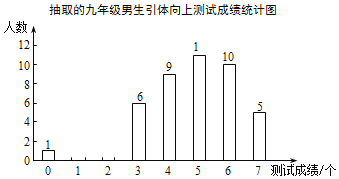
【题目】某中学九年级男生共250人,现随机抽取了部分九年级男生进行引体向上测试,相关数据的统计图如下.设学生引体向上测试成绩为x(单位:个).学校规定:当0≤x<2时成绩等级为不及格,当2≤x<4时成绩等级为及格,当4≤x<6时成绩等级为良好,当x≥6时成绩等级为优秀.样本中引体向上成绩优秀的人数占30%,成绩为1个和2个的人数相同.
(1)补全统计图;
(2)估计全校九年级男生引体向上测试不及格的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
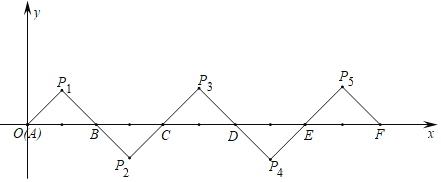
【题目】如图所示,在平面直角坐标系中,![]() ,
,![]() ,
,![]() 是等腰直角三角形且
是等腰直角三角形且![]() ,把
,把![]() 绕点B顺时针旋转
绕点B顺时针旋转![]() ,得到
,得到![]() ,把
,把![]() 绕点C顺时针旋转
绕点C顺时针旋转![]() ,得到
,得到![]() ,依此类推,得到的等腰直角三角形的直角顶点
,依此类推,得到的等腰直角三角形的直角顶点![]() 的坐标为__________.
的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 两点,与
两点,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,点
,点![]() 是第一象限抛物线上的点,连结
是第一象限抛物线上的点,连结![]() 交直线
交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐为
的横坐为![]() ,
,![]() 与
与![]() 的比值为
的比值为![]() .
.
(1)![]() __________;
__________;
(2)当![]() 取最大值时,
取最大值时, __________.
__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
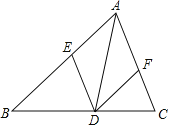
【题目】如图AD是△ABC的角平分线,过点D分别作AC、AB的平行线,交AB于点E,交AC于点F.
(1)求证:四边形AEDF是菱形.
(2)若AF=13,AD=24.求四边形AEDF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
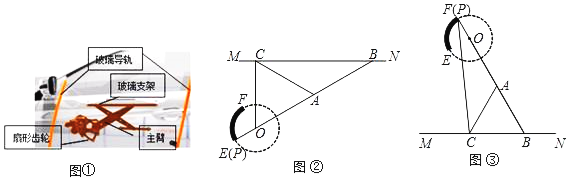
【题目】我们常见的汽车玻璃升降器如图①所示,图②和图③是升降器的示意图,其原理可以看作是主臂PB绕固定的点O旋转,当端点P在固定的扇形齿轮![]() 上运动时,通过叉臂式结构(点B可在MN上滑动)的玻璃支架MN带动玻璃沿导轨作上下运动而达到玻璃升降目的.点O和点P,A,B在同一直线上.当点P与点E重合时,窗户完全闭合(图②),此时∠ABC=30°;当点P与点F重合时,窗户完全打开(图③).已知
上运动时,通过叉臂式结构(点B可在MN上滑动)的玻璃支架MN带动玻璃沿导轨作上下运动而达到玻璃升降目的.点O和点P,A,B在同一直线上.当点P与点E重合时,窗户完全闭合(图②),此时∠ABC=30°;当点P与点F重合时,窗户完全打开(图③).已知![]() 的半径OP=5cm,
的半径OP=5cm,![]() =
=![]() cm,OA=AB=AC=20cm.
cm,OA=AB=AC=20cm.
(1)当窗户完全闭合时,OC=_____cm.
(2)当窗户完全打开时,PC=_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于某点
中,对于某点![]() (
(![]() 不是原点),称以点
不是原点),称以点![]() 为圆心,
为圆心,![]() 长为半径的圆为点
长为半径的圆为点![]() 的半长圆;对于点
的半长圆;对于点![]() ,若将点
,若将点![]() 的半长圆
的半长圆![]() 绕原点旋转,能够使得点
绕原点旋转,能够使得点![]() 位于点
位于点![]() 的半长圆内部或圆上,则称点
的半长圆内部或圆上,则称点![]() 能被点
能被点![]() 半长捕获(或点
半长捕获(或点![]() 能半长捕获点
能半长捕获点![]() ).
).
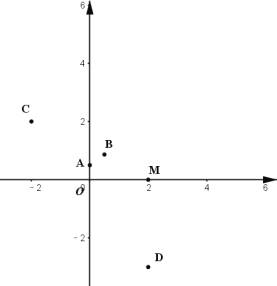
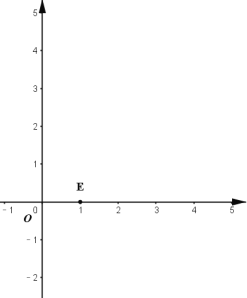
(1)如图,在平面直角坐标系![]() 中,点
中,点![]() ,则点
,则点![]() 的半长圆的面积为__________;下列各点
的半长圆的面积为__________;下列各点![]() 、
、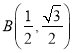 、
、![]() 、
、![]() ,能被点
,能被点![]() 半长捕获的点有__________;
半长捕获的点有__________;
(2)已知点![]() ,
,![]() ,
,![]() ,①如图,点
,①如图,点![]() ,当
,当![]() 时,线段
时,线段![]() 上的所有点均可以被点
上的所有点均可以被点![]() 半长捕获,求
半长捕获,求![]() 的取值范围;②若对于平面上的任意点(原点除外)都不能半长捕获线段
的取值范围;②若对于平面上的任意点(原点除外)都不能半长捕获线段![]() 上的所有点,直接写出
上的所有点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在开发区建设中,要拆除烟囱AB,在地面上事先画定以B为圆心,半径与AB等长的圆形危险区,现在从离B点21米远的建筑物CD顶点C,测得A点的仰角为![]() ,B点的俯角为
,B点的俯角为![]() ,问离B点35米远的文物保护区是否在危险区内,请通过计算说明.
,问离B点35米远的文物保护区是否在危险区内,请通过计算说明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com