
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЖдгкФГЕу
жаЃЌЖдгкФГЕу![]() ЃЈ
ЃЈ![]() ВЛЪЧдЕуЃЉЃЌГЦвдЕу
ВЛЪЧдЕуЃЉЃЌГЦвдЕу![]() ЮЊдВаФЃЌ
ЮЊдВаФЃЌ![]() ГЄЮЊАыОЖЕФдВЮЊЕу
ГЄЮЊАыОЖЕФдВЮЊЕу![]() ЕФАыГЄдВЃЛЖдгкЕу
ЕФАыГЄдВЃЛЖдгкЕу![]() ЃЌШєНЋЕу
ЃЌШєНЋЕу![]() ЕФАыГЄдВ
ЕФАыГЄдВ![]() ШЦдЕуа§зЊЃЌФмЙЛЪЙЕУЕу
ШЦдЕуа§зЊЃЌФмЙЛЪЙЕУЕу![]() ЮЛгкЕу
ЮЛгкЕу![]() ЕФАыГЄдВФкВПЛђдВЩЯЃЌдђГЦЕу
ЕФАыГЄдВФкВПЛђдВЩЯЃЌдђГЦЕу![]() ФмБЛЕу
ФмБЛЕу![]() АыГЄВЖЛёЃЈЛђЕу
АыГЄВЖЛёЃЈЛђЕу![]() ФмАыГЄВЖЛёЕу
ФмАыГЄВЖЛёЕу![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ1ЃЉШчЭМЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЕу
жаЃЌЕу![]() ЃЌдђЕу
ЃЌдђЕу![]() ЕФАыГЄдВЕФУцЛ§ЮЊ__________ЃЛЯТСаИїЕу
ЕФАыГЄдВЕФУцЛ§ЮЊ__________ЃЛЯТСаИїЕу![]() ЁЂ
ЁЂ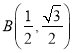 ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌФмБЛЕу
ЃЌФмБЛЕу![]() АыГЄВЖЛёЕФЕуга__________ЃЛ
АыГЄВЖЛёЕФЕуга__________ЃЛ
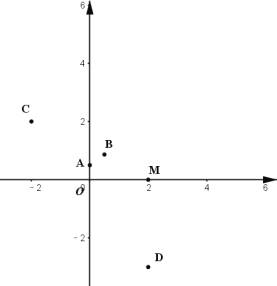
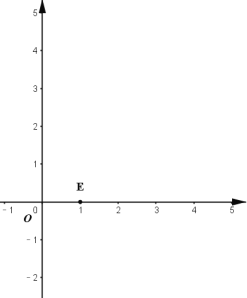
ЃЈ2ЃЉвбжЊЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЂйШчЭМЃЌЕу
ЃЌЂйШчЭМЃЌЕу![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌЯпЖЮ
ЪБЃЌЯпЖЮ![]() ЩЯЕФЫљгаЕуОљПЩвдБЛЕу
ЩЯЕФЫљгаЕуОљПЩвдБЛЕу![]() АыГЄВЖЛёЃЌЧѓ
АыГЄВЖЛёЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЛЂкШєЖдгкЦНУцЩЯЕФШЮвтЕуЃЈдЕуГ§ЭтЃЉЖМВЛФмАыГЄВЖЛёЯпЖЮ
ЕФШЁжЕЗЖЮЇЃЛЂкШєЖдгкЦНУцЩЯЕФШЮвтЕуЃЈдЕуГ§ЭтЃЉЖМВЛФмАыГЄВЖЛёЯпЖЮ![]() ЩЯЕФЫљгаЕуЃЌжБНгаДГі
ЩЯЕФЫљгаЕуЃЌжБНгаДГі![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉS=ІаЃЌBЁЂCСНЕуЃЛЃЈ2ЃЉЂйЃ2ЁмnЁм![]() Лђ
Лђ![]() Ём6nЁм2ЃЛЃЈ2ЃЉЂк
Ём6nЁм2ЃЛЃЈ2ЃЉЂк![]() ЃМtЃМ
ЃМtЃМ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЖЈвхЃЌАыОЖЮЊ1ЃЌжБНгЧѓУцЛ§ЃЛИљОнБЛВЖЛёЕФЖЈвхЃЌЩшЕуЕНдВаФЕФОрРыЮЊdЃЌжЛашrЁмdЁм3rЃЌМДПЩвдВЖЛёЃЛ
ЃЈ2ЃЉЂйРћгУrЁмdЁм3rетИіаджЪЃЌЗжБ№МЦЫуСйНчЕуЃКЕуEКЭЕуFФмЙЛБЛВЖЛёЕФЗЖЮЇЃЌШЛКѓШЅЙЋЙВВПЗжМДПЩЃЛ
ЃЈ2ЃЉЂкдкЩЯвЛЮЪЕФЛљДЁЩЯЃЌжЛашНтЕУЕФВЛЕШЪНЮоЙЋЙВВПЗжЃЌдђВЛФмВЖЛё
ЃЈ1ЃЉЁпЕу![]()
ЁрдВЕФАыОЖЮЊ1ЃЌУцЛ§ЮЊІа
ИљОнБЛВЖЛёЕФЖЈвхЃЌЩшЕуЕНдВаФЕФОрРыЮЊdЃЌжЛашrЁмdЁм3rЃЌМДПЩвдВЖЛё
МДЕБ1ЁмdЁм3ЪБЃЌЕуПЩБЛВЖЛё
![]() ЃЌдђd=
ЃЌдђd=![]() ЃЌВЛЗћКЯЃЛ
ЃЌВЛЗћКЯЃЛ
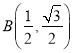 ЃЌd=2ЃЌЗћКЯЃЛ
ЃЌd=2ЃЌЗћКЯЃЛ
![]() ЃЌd=2
ЃЌd=2![]() ЃЌЗћКЯЃЛ
ЃЌЗћКЯЃЛ
![]() ЃЌd=
ЃЌd=![]() ЃЌВЛЗћКЯ
ЃЌВЛЗћКЯ
ЃЈ2ЃЉЂйЁпЕуN(0ЃЌn)
ЁрдВЕФАыОЖЮЊ![]() ЃЌЫљвджЛашТњзу
ЃЌЫљвджЛашТњзу![]() ЁмdЁм
ЁмdЁм![]() ЪБЃЌдђПЩБЛВЖЛё
ЪБЃЌдђПЩБЛВЖЛё
ЕуE(1ЃЌ0)ЃЌдђd=1ЃЌвЊЯыФмЙЛБЛВЖЛёЃЌдђЃК
![]() Ём1Ём
Ём1Ём![]()
НтЕУЃК![]() ЁмnЁм
ЁмnЁм![]() Лђ
Лђ![]() ЁмnЁм
ЁмnЁм![]()
ЕуF(1ЃЌ![]() )ЃЌдђd=2
)ЃЌдђd=2
ЭЌРэЃЌ![]() Ём2Ём
Ём2Ём![]()
НтЕУЃК![]() ЁмnЁм
ЁмnЁм![]() Лђ
Лђ![]() ЁмnЁм
ЁмnЁм![]()
КЯВЂЕУЃК![]() ЁмnЁм
ЁмnЁм![]() Лђ
Лђ![]() ЁмnЁм
ЁмnЁм![]()
ЃЈ2ЃЉЂкЭЌЩЯЃЌдВЕФАыОЖЮЊ![]() ЃЌЫљвджЛашТњзу
ЃЌЫљвджЛашТњзу![]() ЁмdЁм
ЁмdЁм![]() ЪБЃЌдђПЩБЛВЖЛё
ЪБЃЌдђПЩБЛВЖЛё
ЕуE(tЃЌ0)ЃЌдђd=tЃЌвЊЯыФмЙЛБЛВЖЛёЃЌдђЃК![]() ЁмnЁм
ЁмnЁм![]() Лђ
Лђ![]() ЁмnЁм
ЁмnЁм![]()
ЕуF(tЃЌ![]() )ЃЌдђd=
)ЃЌдђd=![]() ЃЌвЊЯыФмЙЛБЛВЖЛёЃЌдђЃК
ЃЌвЊЯыФмЙЛБЛВЖЛёЃЌдђЃК![]() ЁмnЁм
ЁмnЁм![]() Лђ
Лђ![]() ЁмnЁм
ЁмnЁм![]()
ЁпШЮвтжЕЖМВЛФмВЖЛёЃЌЁрЕУЕНЕФСНИіВЛЕШЪНЮоЙЋЙВВПЗжЃЌМДЃК
![]() КЭ
КЭ![]() ЃО
ЃО![]()
дкНсКЯtЃО0ЃЌНтЕУЃК0ЃМtЃМ![]()



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
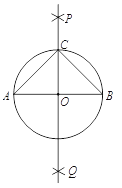
ЁОЬтФПЁПЯТУцЪЧЁАзївдвбжЊЯпЖЮЮЊаББпЕФЕШбќжБНЧШ§НЧаЮЁБЕФГпЙцзїЭМЙ§ГЬЃЎ
вбжЊЃКЯпЖЮ![]() ЃЎ
ЃЎ
![]()
ЧѓзїЃКвд![]() ЮЊаББпЕФвЛИіЕШбќжБНЧШ§НЧаЮ
ЮЊаББпЕФвЛИіЕШбќжБНЧШ§НЧаЮ![]() ЃЎ
ЃЎ
зїЗЈЃКШчЭМЃЌ
ЃЈ1ЃЉЗжБ№вдЕу![]() КЭЕу
КЭЕу![]() ЮЊдВаФЃЌДѓгк
ЮЊдВаФЃЌДѓгк![]() ЕФГЄЮЊАыОЖзїЛЁЃЌСНЛЁЯрНЛгк
ЕФГЄЮЊАыОЖзїЛЁЃЌСНЛЁЯрНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЛ
СНЕуЃЛ
ЃЈ2ЃЉзїжБЯп![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЛ
ЃЛ
ЃЈ3ЃЉвд![]() ЮЊдВаФЃЌ
ЮЊдВаФЃЌ![]() ЕФГЄЮЊАыОЖзїдВЃЌНЛжБЯп
ЕФГЄЮЊАыОЖзїдВЃЌНЛжБЯп![]() гкЕу
гкЕу![]() ЃЛ
ЃЛ
ЃЈ4ЃЉСЌНг![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
дђ![]() МДЮЊЫљЧѓзїЕФШ§НЧаЮЃЎ
МДЮЊЫљЧѓзїЕФШ§НЧаЮЃЎ
ЧыЛиД№ЃКдкЩЯУцЕФзїЭМЙ§ГЬжаЃЌЂй![]() ЪЧжБНЧШ§НЧаЮЕФвРОнЪЧ________ЃЛЂк
ЪЧжБНЧШ§НЧаЮЕФвРОнЪЧ________ЃЛЂк![]() ЪЧЕШбќШ§НЧаЮЕФвРОнЪЧ__________ЃЎ
ЪЧЕШбќШ§НЧаЮЕФвРОнЪЧ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
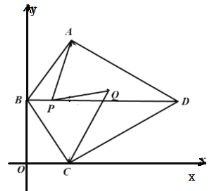
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЖдНЧЯп
ЃЌЖдНЧЯп![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() жсЩЯЃЌ
жсЩЯЃЌ![]() гы
гы![]() жсЦНааЃЌЕу
жсЦНааЃЌЕу![]() дк
дк![]() жсЩЯЃЎ
жсЩЯЃЎ
ЃЈ1ЃЉЧѓ![]() ЕФЖШЪ§ЃЎ
ЕФЖШЪ§ЃЎ
ЃЈ2ЃЉЕу![]() дкЖдНЧЯп
дкЖдНЧЯп![]() ЩЯЃЌЕу
ЩЯЃЌЕу![]() дкЫФБпаЮ
дкЫФБпаЮ![]() ФкЧвдкЕу
ФкЧвдкЕу![]() ЕФгвБпЃЌСЌНг
ЕФгвБпЃЌСЌНг![]() ЃЌвбжЊ
ЃЌвбжЊ![]() ЃЌ
ЃЌ![]() ЃЌЩш
ЃЌЩш![]() ЃЎ
ЃЎ
ЂйЧѓ![]() ЕФГЄЃЈгУКЌ
ЕФГЄЃЈгУКЌ![]() ЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЂкШєФГвЛЗДБШР§КЏЪ§ЭМЯѓЭЌЪБОЙ§Еу![]() ЁЂ
ЁЂ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
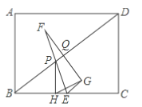
ЁОЬтФПЁПШчЭМЃЌдкОиаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌЕу
ЕФжаЕуЃЌЕу![]() ЮЊЖдНЧЯп
ЮЊЖдНЧЯп![]() ЩЯЕФЖЏЕуЃЌЩш
ЩЯЕФЖЏЕуЃЌЩш![]() ЃЌзї
ЃЌзї![]() гкЕу
гкЕу![]() ЃЌСЌНс
ЃЌСЌНс![]() ВЂбгГЄжСЕу
ВЂбгГЄжСЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЌзїЕу
ЃЌзїЕу![]() Йигк
Йигк![]() ЕФЖдГЦЕу
ЕФЖдГЦЕу![]() ЃЌ
ЃЌ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌСЌНс
ЃЌСЌНс![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБЕу![]() дЫЖЏЕНЖдНЧЯп
дЫЖЏЕНЖдНЧЯп![]() ЕФжаЕуЪБЃЌЧѓ
ЕФжаЕуЪБЃЌЧѓ![]() ЕФжмГЄЃЛ
ЕФжмГЄЃЛ
ЃЈ3ЃЉдкЕу![]() ЕФдЫЖЏЕФЙ§ГЬжаЃЌ
ЕФдЫЖЏЕФЙ§ГЬжаЃЌ![]() ЪЧЗёПЩвдЮЊЕШбќШ§НЧаЮЃПШєПЩвдЃЌЧѓГі
ЪЧЗёПЩвдЮЊЕШбќШ§НЧаЮЃПШєПЩвдЃЌЧѓГі![]() ЕФжЕЃЛШєВЛПЩвдЃЌЫЕУїРэгЩЃЎ
ЕФжЕЃЛШєВЛПЩвдЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫЕїВщбЇЩњЖдРЌЛјЗжРрМАЭЖЗХжЊЪЖЕФСЫНтЧщПіЃЌДгМзЁЂввСНаЃИїЫцЛњГщШЁ40УћбЇЩњНјааСЫЯрЙижЊЪЖВтЪдЃЌЛёЕУСЫЫћУЧЕФГЩМЈЃЈАйЗжжЦЃЉЃЌВЂЖдЪ§ОнЃЈГЩМЈЃЉНјааСЫећРэЁЂУшЪіКЭЗжЮіЃЎЯТУцИјГіСЫВПЗжаХЯЂЃЎ
aЃЎМзЁЂввСНаЃ40УћбЇЩњГЩМЈЕФЦЕЪ§ЗжВМЭГМЦБэШчЯТЃК
ГЩМЈx бЇаЃ |
|
|
|
|
|
Мз | 4 | 11 | 13 | 10 | 2 |
вв | 6 | 3 | 15 | 14 | 2 |
ЃЈЫЕУїЃКГЩМЈ80ЗжМАвдЩЯЮЊгХауЃЌ70~79ЗжЮЊСМКУЃЌ60~69ЗжЮЊКЯИёЃЌ60ЗжвдЯТЮЊВЛКЯИёЃЉ
bЃЎМзаЃГЩМЈдк![]() етвЛзщЕФЪЧЃК
етвЛзщЕФЪЧЃК
70 70 70 71 72 73 73 73 74 75 76 77 78
cЃЎМзЁЂввСНаЃГЩМЈЕФЦНОљЗжЁЂжаЮЛЪ§ЁЂжкЪ§ШчЯТЃК
бЇаЃ | ЦНОљЗж | жаЮЛЪ§ | жкЪ§ |
Мз | 74.2 | n | 5 |
вв | 73.5 | 76 | 84 |
ИљОнвдЩЯаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉаДГіБэжаnЕФжЕЃЛ
ЃЈ2ЃЉдкДЫДЮВтЪджаЃЌФГбЇЩњЕФГЩМЈЪЧ74ЗжЃЌдкЫћЫљЪєбЇаЃХХдкЧА20УћЃЌгЩБэжаЪ§ОнПЩжЊИУбЇЩњЪЧ_____________аЃЕФбЇЩњЃЈЬюЁАМзЁБЛђЁАввЁБЃЉЃЌРэгЩЪЧ__________ЃЛ
ЃЈ3ЃЉМйЩшвваЃ800УћбЇЩњЖМВЮМгДЫДЮВтЪдЃЌЙРМЦГЩМЈгХауЕФбЇЩњШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
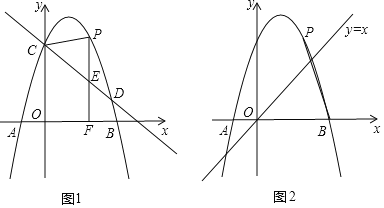
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌвбжЊХзЮяЯп
жаЃЌвбжЊХзЮяЯп![]() .
.
(1)ЧѓХзЮяЯпЕФЖдГЦжс(гУКЌ![]() ЕФЪНзгШЅБэЪО)ЃЛ
ЕФЪНзгШЅБэЪО)ЃЛ
(2)ШєЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЖМдкХзЮяЯп
ЖМдкХзЮяЯп![]() ЩЯЃЌдђ
ЩЯЃЌдђ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЕФДѓаЁЙиЯЕЮЊ_______ЃЛ
ЕФДѓаЁЙиЯЕЮЊ_______ЃЛ
(3)жБЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌгы
ЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зїДЙжБгк
зїДЙжБгк![]() жсЕФжБЯп
жсЕФжБЯп![]() гыХзЮяЯп
гыХзЮяЯп![]() гаСНИіНЛЕуЃЌдкХзЮяЯпЖдГЦжсгвВрЕФЕуМЧЮЊ
гаСНИіНЛЕуЃЌдкХзЮяЯпЖдГЦжсгвВрЕФЕуМЧЮЊ![]() ЃЌЕБ
ЃЌЕБ![]() ЮЊЖлНЧШ§НЧаЮЪБЃЌЧѓ
ЮЊЖлНЧШ§НЧаЮЪБЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
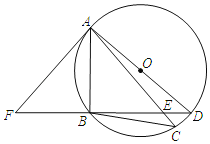
ЁОЬтФПЁПШчЭМЃЌADЪЧЁбOЕФжБОЖЃЌЛЁBAЃНЛЁBCЃЌBDНЛACгкЕуEЃЌЕуFдкDBЕФбгГЄЯпЩЯЃЌЧвЁЯBAFЃНЁЯCЃЎ
ЃЈ1ЃЉЧѓжЄЃКAFЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉЧѓжЄЃКЁїABEЁзЁїDBAЃЛ
ЃЈ3ЃЉШєBDЃН8ЃЌBEЃН6ЃЌЧѓABЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЫљЪОЃЌХзЮяЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() СНЕуЃЌгы
СНЕуЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌжБЯп
ЃЌжБЯп![]() ОЙ§Еу
ОЙ§Еу![]() ЃЌгыХзЮяЯпСэвЛИіНЛЕуЮЊ
ЃЌгыХзЮяЯпСэвЛИіНЛЕуЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЪЧХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЙ§
ЪЧХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЙ§![]() Еузї
Еузї![]() жсгкЕу
жсгкЕу![]() ЃЌНЛжБЯп
ЃЌНЛжБЯп![]() гкЕу
гкЕу![]()
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪН
ЃЈ2ЃЉЕБЕу![]() дкжБЯп
дкжБЯп![]() ЩЯЗНЃЌЧв
ЩЯЗНЃЌЧв![]() ЪЧвд
ЪЧвд![]() ЮЊбќЕФЕШбќШ§НЧаЮЪБЃЌЧѓ
ЮЊбќЕФЕШбќШ§НЧаЮЪБЃЌЧѓ![]() ЕФзјБъ
ЕФзјБъ
ЃЈ3ЃЉШчЭМ2ЫљЪОЃЌШєЕу![]() ЮЊЖдГЦжсгвВрХзЮяЯпЩЯвЛЕуЃЌСЌНг
ЮЊЖдГЦжсгвВрХзЮяЯпЩЯвЛЕуЃЌСЌНг![]() ЃЌвд
ЃЌвд![]() ЮЊжБНЧЖЅЕуЃЌЯпЖЮ
ЮЊжБНЧЖЅЕуЃЌЯпЖЮ![]() ЮЊНЯГЄжБНЧБпЃЌЙЙдьСНжБНЧБпБШЮЊ
ЮЊНЯГЄжБНЧБпЃЌЙЙдьСНжБНЧБпБШЮЊ![]() ЕФ
ЕФ![]() ЃЌЪЧЗёДцдкЕу
ЃЌЪЧЗёДцдкЕу![]() ЃЌЪЙЕу
ЃЌЪЙЕу![]() ЧЁКУТфдкжБЯп
ЧЁКУТфдкжБЯп![]() ЩЯЃПШєДцдкЃЌЧыжБНгаДГіЯргІЕу
ЩЯЃПШєДцдкЃЌЧыжБНгаДГіЯргІЕу![]() ЕФКсзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФКсзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
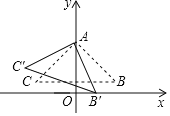
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯCABЃН90ЁуЃЌABЃНACЃЌЕуAдкyжсЩЯЃЌBCЁЮxжсЃЌЕуB![]() ЃЎНЋЁїABCШЦЕуAЫГЪБеыа§зЊЕФЁїABЁфCЁфЃЌЕБЕуBЁфТфдкxжсЕФе§АыжсЩЯЪБЃЌЕуCЁфЕФзјБъЮЊЃЈЁЁЁЁЃЉ
ЃЎНЋЁїABCШЦЕуAЫГЪБеыа§зЊЕФЁїABЁфCЁфЃЌЕБЕуBЁфТфдкxжсЕФе§АыжсЩЯЪБЃЌЕуCЁфЕФзјБъЮЊЃЈЁЁЁЁЃЉ
A.ЃЈЉ![]() ЃЌ
ЃЌ![]() Љ1ЃЉB.ЃЈЉ
Љ1ЃЉB.ЃЈЉ![]() ЃЌ
ЃЌ![]() Љ1ЃЉ
Љ1ЃЉ
C.ЃЈЉ![]() ЃЌ
ЃЌ![]() +1ЃЉD.ЃЈЉ
+1ЃЉD.ЃЈЉ![]() ЃЌ
ЃЌ![]() Љ1ЃЉ
Љ1ЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com