练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

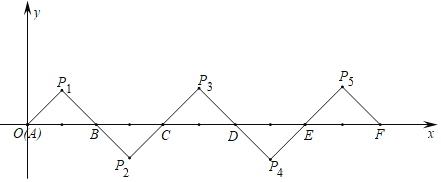
    【题目】如图所示，在平面直角坐标系中，，，是等腰直角三角形且，把绕点B顺时针旋转，得到，把绕点C顺时针旋转，得到，依此类推，得到的等腰直角三角形的直角顶点的坐标为__________．

    【答案】

    【解析】

    根据题意可以求得P2的纵坐标为﹣1，P3的纵坐标为1，P4的纵坐标为﹣1，P5的纵坐标为1，…，从而发现其中的变化的规律，从而可以求得P2019的坐标．

    作P1⊥x轴于H．

    ∵A（0，0），B（2，0），∴AB=2．

    ∵△AP1B是等腰直角三角形，∴P1HAB=1，AH=BH=1，∴P1的纵坐标为1．

    ∵△AP1B绕点B顺时针旋转180°，得到△BP2C；把△BP2C绕点C顺时针旋转180°，得到△CP3D，∴P2的纵坐标为﹣1，P3的纵坐标为1，P4的纵坐标为﹣1，P5的纵坐标为1，…，∴P2019的纵坐标为1，横坐标为2019×2﹣1=4037，即P2019（4037，1）．

    故答案为：（4037，1）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某学校八、九两个年级各有学生180人，为了解这两个年级学生的体质健康情况，进行了抽样调查，具体过程如下：

    　　收集数据

    从八、九两个年级各随机抽取20名学生进行体质健康测试，测试成绩（百分制）如下：

    八年级

    78

    86

    74

    81

    75

    76

    87

    70

    75

    90

    75

    79

    81

    70

    74

    80

    86

    69

    83

    77

    九年级

    93

    73

    88

    81

    72

    81

    94

    83

    77

    83

    80

    81

    70

    81

    73

    78

    82

    80

    70

    40

    整理、描述数据

    将成绩按如下分段整理、描述这两组样本数据：

    成绩（x）

    40≤x≤49

    50≤x≤59

    60≤x≤69

    70≤x≤79

    80≤x≤89

    90≤x≤100

    八年级人数

    0

    0

    1

    11

    7

    1

    九年级人数

    1

    0

    0

    7

    10

    2

    （说明：成绩80分及以上为体质健康优秀，70～79分为体质健康良好，60～69分为体质健康合格，60分以下为体质健康不合格）

    　　分析数据

    两组样本数据的平均数、中位数、众数、方差如表所示：

    年级

    平均数

    中位数

    众数

    方差

    八年级

    78.3

    77.5

    75

    33.6

    九年级

    78

    80.5

    a

    52.1

    （1）表格中a的值为______；

    （2）请你估计该校九年级体质健康优秀的学生人数为多少？

    （3）根据以上信息，你认为哪个年级学生的体质健康情况更好一些？请说明理由．（请从两个不同的角度说明推断的合理性）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面是“作以已知线段为斜边的等腰直角三角形”的尺规作图过程．

    已知：线段．

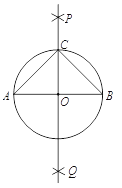
    求作：以为斜边的一个等腰直角三角形．

    作法：如图，

    （1）分别以点和点为圆心，大于的长为半径作弧，两弧相交于，两点；

    （2）作直线，交于点；

    （3）以为圆心，的长为半径作圆，交直线于点；

    （4）连接，．

    则即为所求作的三角形．

    请回答：在上面的作图过程中，①是直角三角形的依据是________；②是等腰三角形的依据是__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数学概念

    在两个等腰三角形中，如果其中一个三角形的底边长和底角的度数分别等于另一个三角形的腰长和顶角的度数，那么称这两个等腰三角形互为姊妹三角形．

    概念理解

    （1）如图①，在△ABC中，AB＝AC，请用直尺和圆规作出它的姊妹三角形（保留作图痕迹，不写作法）．

    特例分析

    （2）①在△ABC中，AB＝AC，∠A＝30°，，求它的姊妹三角形的顶角的度数和腰长；

    ②如图②，在△ABC中，AB＝AC，D是AC上一点，连接BD．若△ABC与△ABD互为姊妹三角形，且△ABC∽△BCD，则∠A＝　 　°．

    深入研究

    （3）下列关于姊妹三角形的结论：

    ①每一个等腰三角形都有姊妹三角形；

    ②等腰三角形的姊妹三角形是锐角三角形；

    ③如果两个等腰三角形互为姊妹三角形，那么这两个三角形可能全等；

    ④如果一个等腰三角形存在两个不同的姊妹三角形，那么这两个三角形也一定互为姊妹三角形．

    其中所有正确结论的序号是　 　．

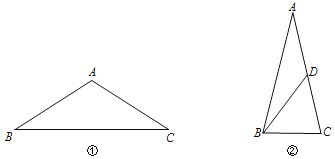
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线与轴交于点，直线：交轴于点，交直线点．

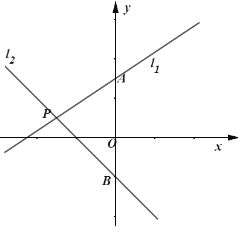
    （1）求直线的函数解析式；

    （2）过动点作轴的垂线与直线、分别交于、两点，且．

    ①求的取值范围；

    ②若，直接写出的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线的对称轴为直线，图象过点，部分图象如图所示，下列判断：①；②；③；④若点，均在抛物线上，则，其中正确的个数是（ ）

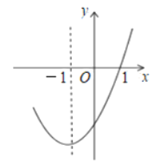
    A.1B.2C.3D.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

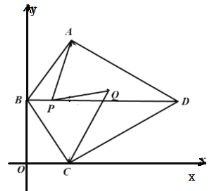
    【题目】如图，在四边形中，，，对角线，点在轴上，与轴平行，点在轴上．

    （1）求的度数．

    （2）点在对角线上，点在四边形内且在点的右边，连接，已知，，设．

    ①求的长（用含的代数式表示）；

    ②若某一反比例函数图象同时经过点、，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

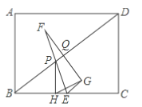
    【题目】如图，在矩形中，，点是的中点，点为对角线上的动点，设，作于点，连结并延长至点，使得，作点关于的对称点，交于点，连结．

    （1）求证：；

    （2）当点运动到对角线的中点时，求的周长；

    （3）在点的运动的过程中，是否可以为等腰三角形？若可以，求出的值；若不可以，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

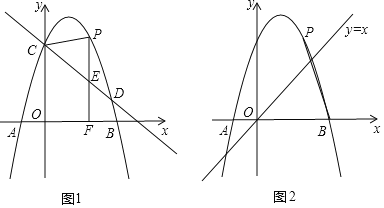
    【题目】如图1所示，抛物线与轴交于点两点，与轴交于点，直线经过点，与抛物线另一个交点为，点是抛物线上的一个动点，过点作轴于点，交直线于点

    （1）求抛物线的解析式

    （2）当点在直线上方，且是以为腰的等腰三角形时，求的坐标

    （3）如图2所示，若点为对称轴右侧抛物线上一点，连接，以为直角顶点，线段为较长直角边，构造两直角边比为的，是否存在点，使点恰好落在直线上？若存在，请直接写出相应点的横坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案