
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() :
:![]() 交
交![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 点
点![]() .
.
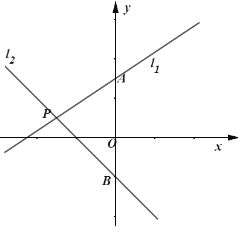
(1)求直线![]() 的函数解析式;
的函数解析式;
(2)过动点![]() 作
作![]() 轴的垂线与直线
轴的垂线与直线![]() 、
、![]() 分别交于
分别交于![]() 、
、![]() 两点,且
两点,且![]() .
.
①求![]() 的取值范围;
的取值范围;
②若![]() ,直接写出
,直接写出![]() 的值.
的值.
【答案】(1)![]() ;(2)①
;(2)①![]() 且
且![]() ;②
;② ![]() 或
或![]()
【解析】
(1)利用![]() 求出
求出![]() 点坐标为
点坐标为![]() ,再设直线
,再设直线![]() 的函数解析式为y=kx+b,将点A、P的坐标代入解答;
的函数解析式为y=kx+b,将点A、P的坐标代入解答;
(2)①由已知可得:![]() 、
、![]() 两点的坐标分别为:
两点的坐标分别为:![]() ,
,![]() ,分两种情况:当点
,分两种情况:当点![]() 在点
在点![]() 右侧时,点
右侧时,点![]() 在点
在点![]() 的上方,求出
的上方,求出![]() 解得
解得![]() ,当点
,当点![]() 在点
在点![]() 左侧时,点
左侧时,点![]() 在点
在点![]() 的下方,求得
的下方,求得![]() 解得
解得![]() ,由此动点a的取值范围;
,由此动点a的取值范围;
②设![]() ,连接AN1,作N1D⊥y轴于D,PC⊥y轴于C,根据
,连接AN1,作N1D⊥y轴于D,PC⊥y轴于C,根据![]() ,求出OD=1+3=4,由此得到点N1的横坐标是-6,即a=-6;设
,求出OD=1+3=4,由此得到点N1的横坐标是-6,即a=-6;设![]() ,,连接AN2,作N2D⊥y轴于D,PC⊥y轴于C,根据
,,连接AN2,作N2D⊥y轴于D,PC⊥y轴于C,根据![]() ,求出CD=
,求出CD=![]() CB=1,得到点N2的纵坐标是0,由此解得x=-2,得到a=-2.
CB=1,得到点N2的纵坐标是0,由此解得x=-2,得到a=-2.
(1)将点P的坐标代入![]() 中,得t=3-2=1,
中,得t=3-2=1,
∴![]() 点坐标为
点坐标为![]() ,
,
设直线![]() 的函数解析式为y=kx+b,将点A、P的坐标代入,得
的函数解析式为y=kx+b,将点A、P的坐标代入,得
![]() ,解得
,解得![]() ,
,
∴直线![]() 的函数解析式为
的函数解析式为![]() ;
;
(2)①由已知可得:![]() 、
、![]() 两点的坐标分别为:
两点的坐标分别为:![]() ,
,![]() ,
,
当点![]() 在点
在点![]() 右侧时,点
右侧时,点![]() 在点
在点![]() 的上方,
的上方,
∴![]() 解得
解得![]() ,
,
当点![]() 在点
在点![]() 左侧时,点
左侧时,点![]() 在点
在点![]() 的下方,
的下方,
∴![]() 解得
解得![]() ,
,
综上![]() 的取值范围是:
的取值范围是:![]() 且
且![]() (注:没有
(注:没有![]() 不扣分);
不扣分);
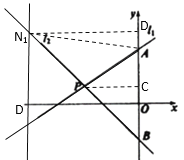
②设![]() ,连接AN1,作N1D⊥y轴于D,PC⊥y轴于C,
,连接AN1,作N1D⊥y轴于D,PC⊥y轴于C,
∵![]() ,
,
∴N1P=PB,
∵B(0,-2),
∴CD=CB=1-(-2)=3,
∴OD=1+3=4,
将y=4代入y=-x-2中得-x-2=4,
解得x=-6,
∴点N1的横坐标是-6,即a=-6;
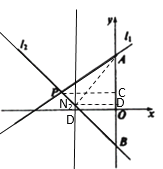
设![]() ,连接AN2,作N2D⊥y轴于D,PC⊥y轴于C,
,连接AN2,作N2D⊥y轴于D,PC⊥y轴于C,
∵![]() ,
,
∴PN2=![]() PB,
PB,
∴CD=![]() CB=1,
CB=1,
∴点N2的纵坐标是0,
将y=0代入y=-x-2中,得x=-2,
∴a=-2,
综上,![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
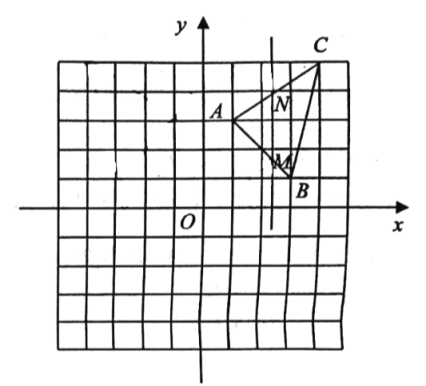
【题目】如图,在平面直角坐标系中,点![]() ,点
,点![]() ,点
,点![]() .
.
(1)画出![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() ,并写出点
,并写出点![]() 的对称点
的对称点![]() 的坐标;
的坐标;
(2)若点![]() 在
在![]() 轴上,连接
轴上,连接![]() 、
、![]() ,则
,则![]() 的最小值是 ;
的最小值是 ;
(3)若直线![]() 轴,与线段
轴,与线段![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() (点
(点![]() 不与点
不与点![]() 重合),若将
重合),若将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 的对称点为点
的对称点为点![]() ,当点
,当点![]() 落在
落在![]() 的内部(包含边界)时,点
的内部(包含边界)时,点 的横坐标
的横坐标![]() 的取值范围是 .
的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P(2,﹣3)在抛物线L:y=ax2﹣2ax+a+k(a,k均为常数且a≠0)上,L交y轴于点C,连接CP.
(1)用a表示k,并求L的对称轴;
(2)当L经过点(4,﹣7)时,求此时L的表达式及其顶点坐标;
(3)横,纵坐标都是整数的点叫做整点.如图,当a<0时,若L在点C,P之间的部分与线段CP所围成的区域内(不含边界)恰有5个整点,求a的取值范围;
(4)点M(x1,y1),N(x2,y2)是L上的两点,若t≤x1≤t+1,当x2≥3时,均有y1≥y2,直接写出t的取值范围.
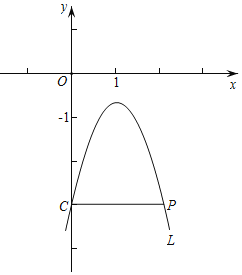
查看答案和解析>>
科目:初中数学 来源: 题型:
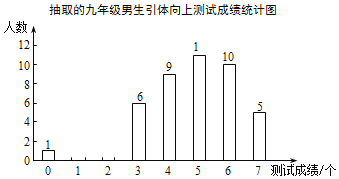
【题目】某中学九年级男生共250人,现随机抽取了部分九年级男生进行引体向上测试,相关数据的统计图如下.设学生引体向上测试成绩为x(单位:个).学校规定:当0≤x<2时成绩等级为不及格,当2≤x<4时成绩等级为及格,当4≤x<6时成绩等级为良好,当x≥6时成绩等级为优秀.样本中引体向上成绩优秀的人数占30%,成绩为1个和2个的人数相同.
(1)补全统计图;
(2)估计全校九年级男生引体向上测试不及格的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
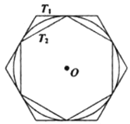
【题目】如图,有一个圆![]() 和两个正六边形
和两个正六边形![]() ,
,![]() .
.![]() 的6个顶点都在圆周上,
的6个顶点都在圆周上,![]() 的6条边都和圆
的6条边都和圆![]() 相切(我们称
相切(我们称![]() ,
,![]() 分别为圆
分别为圆![]() 的外切正六边形和内接正六边形),若设
的外切正六边形和内接正六边形),若设![]() ,
,![]() 的周长分别为
的周长分别为![]() ,
,![]() ,圆
,圆![]() 的半径为
的半径为![]() ,则
,则![]() ___;
___;![]() ____;正六边形
____;正六边形![]() ,
,![]() 的面积比
的面积比![]() 的值是____.
的值是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
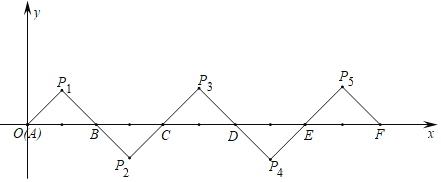
【题目】如图所示,在平面直角坐标系中,![]() ,
,![]() ,
,![]() 是等腰直角三角形且
是等腰直角三角形且![]() ,把
,把![]() 绕点B顺时针旋转
绕点B顺时针旋转![]() ,得到
,得到![]() ,把
,把![]() 绕点C顺时针旋转
绕点C顺时针旋转![]() ,得到
,得到![]() ,依此类推,得到的等腰直角三角形的直角顶点
,依此类推,得到的等腰直角三角形的直角顶点![]() 的坐标为__________.
的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 两点,与
两点,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,点
,点![]() 是第一象限抛物线上的点,连结
是第一象限抛物线上的点,连结![]() 交直线
交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐为
的横坐为![]() ,
,![]() 与
与![]() 的比值为
的比值为![]() .
.
(1)![]() __________;
__________;
(2)当![]() 取最大值时,
取最大值时, __________.
__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
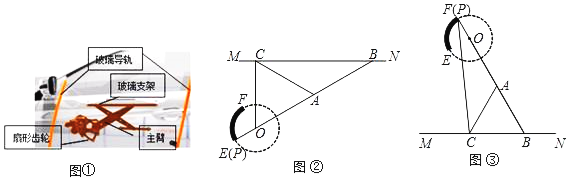
【题目】我们常见的汽车玻璃升降器如图①所示,图②和图③是升降器的示意图,其原理可以看作是主臂PB绕固定的点O旋转,当端点P在固定的扇形齿轮![]() 上运动时,通过叉臂式结构(点B可在MN上滑动)的玻璃支架MN带动玻璃沿导轨作上下运动而达到玻璃升降目的.点O和点P,A,B在同一直线上.当点P与点E重合时,窗户完全闭合(图②),此时∠ABC=30°;当点P与点F重合时,窗户完全打开(图③).已知
上运动时,通过叉臂式结构(点B可在MN上滑动)的玻璃支架MN带动玻璃沿导轨作上下运动而达到玻璃升降目的.点O和点P,A,B在同一直线上.当点P与点E重合时,窗户完全闭合(图②),此时∠ABC=30°;当点P与点F重合时,窗户完全打开(图③).已知![]() 的半径OP=5cm,
的半径OP=5cm,![]() =
=![]() cm,OA=AB=AC=20cm.
cm,OA=AB=AC=20cm.
(1)当窗户完全闭合时,OC=_____cm.
(2)当窗户完全打开时,PC=_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校开展“书香校园”活动以来,受到同学们的广泛关注,学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如图不完整的统计表
学生借阅图书的次数
借阅图书的次数 | 0次 | 1次 | 2次 | 3次 | 4次及以上 |
人数 | 7 | 13 | a | 10 | 3 |
学生借阅图书的次数统计表

请你根据统计图表的信息,解答下列问题:
(1)a= ;b=
(2)该调查统计数据的中位数是__________次
(3)扇形统计图中,“3次”所对应的扇形圆心角度数是______________;
(4)若该校共有2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次以上”的人数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com