
【题目】已知点P(2,﹣3)在抛物线L:y=ax2﹣2ax+a+k(a,k均为常数且a≠0)上,L交y轴于点C,连接CP.
(1)用a表示k,并求L的对称轴;
(2)当L经过点(4,﹣7)时,求此时L的表达式及其顶点坐标;
(3)横,纵坐标都是整数的点叫做整点.如图,当a<0时,若L在点C,P之间的部分与线段CP所围成的区域内(不含边界)恰有5个整点,求a的取值范围;
(4)点M(x1,y1),N(x2,y2)是L上的两点,若t≤x1≤t+1,当x2≥3时,均有y1≥y2,直接写出t的取值范围.
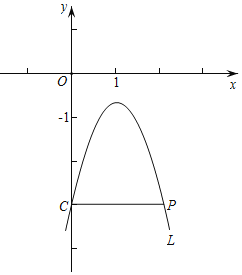
【答案】(1)k=﹣3﹣a,x=1;(2)y=﹣![]() x2+x﹣3,顶点坐标为(1,﹣
x2+x﹣3,顶点坐标为(1,﹣![]() );(3)﹣6≤a<﹣5;(4)﹣1≤t≤2
);(3)﹣6≤a<﹣5;(4)﹣1≤t≤2
【解析】
(1)点![]() 代入抛物线上,则
代入抛物线上,则![]() ;抛物线
;抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,即
,即![]() ;
;
(2)点![]() ,代入抛物线上,则有
,代入抛物线上,则有![]() ,解得
,解得![]() ,
,![]() ,即可求解;
,即可求解;
(3)顶点坐标![]() ,
,![]() 时在指定区域内有5个整数点;
时在指定区域内有5个整数点;
(4)当![]() 时,
时,![]() 或
或![]() ;当
;当![]() 时,
时,![]() 或
或![]() .
.
解:(1)∵点P(2,﹣3)在抛物线L:y=ax2﹣2ax+a+k(a,k均为常数且a≠0)上,
∴﹣3=4a﹣4a+a+k,
∴k=﹣3﹣a;
抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,即
,即![]() ;
;
(2)∵L经过点(4,﹣7),
∴16a﹣8a+a+k=﹣7,
∵k=﹣3﹣a,
![]() ,解得
,解得![]() ,
,![]() ,
,
∴L的表达式为y=﹣![]() x2+x﹣3;
x2+x﹣3;
![]() ,
,
∴顶点坐标为(1,﹣![]() );
);
(3)顶点坐标(1,﹣a﹣3),
∵在点C,P之间的部分与线段CP所围成的区域内(不含边界)恰有5个整点,
∴2<﹣a﹣3≤3,
∴﹣6≤a<﹣5;
(4)当a>0时,t≥3或t+1≤﹣1,
∴t≥3或t≤﹣2;
代入检验,此时有不符合条件的点使y1≥y2,
故此情况舍去;
当a<0时,t+1≤3且t≥﹣1,
∴﹣1≤t≤2;
综上所述,﹣1≤t≤2;


科目:初中数学 来源: 题型:
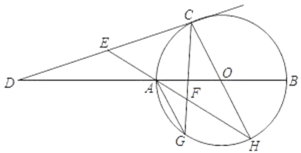
【题目】如图,已知AB为⊙O的直径,C为⊙O上异于A、B的一点,过C点的切线与BA的延长线交于D点,E为CD上一点,连接EA并延长交⊙O于H,F为EH上一点,且EF=CE,CF交延长线交⊙O于G.
(1)求证:弧AG=弧GH;
(2)若E为DC的中点,sim∠CDO=![]() ,AH=2
,AH=2![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
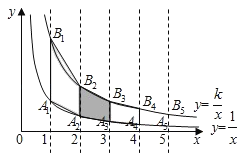
【题目】在滑草过程中,小明发现滑道两边形如两条双曲线,如图,点A1,A2,A3…在反比例函数y=![]() (x>0)的图象上,点B1,B2,B3…反比例函数y=
(x>0)的图象上,点B1,B2,B3…反比例函数y=![]() (k>1,x>0)的图象上,A1B1∥A2B2…∥y轴,已知点A1,A2…的横坐标分别为1,2,…,令四边形A1B1B2A2、A2B2B3A3、…的面积分别为S1、S2、…
(k>1,x>0)的图象上,A1B1∥A2B2…∥y轴,已知点A1,A2…的横坐标分别为1,2,…,令四边形A1B1B2A2、A2B2B3A3、…的面积分别为S1、S2、…
(1)用含k的代数式表示S1=_____.
(2)若S19=39,则k=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:若抛物线的顶点在坐标轴上,则称该抛物线为“数轴函数”例如抛物线y=x2和y=(x-1)2都是“数轴函数”.
(1)抛物线y=x2-4x+4和抛物线y=x2-6x是“数轴函数“吗?请说明理由;
(2)若抛物线y=2x2+4mx+m2+16是“数轴函数”,求该抛物线的表达式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题)若a+b=10,则ab的最大值是多少?
(探究)
探究一:当a﹣b=0时,求ab值.
显然此时,a=b=5,则ab=5×5=25
探究二:当a﹣b=±1时,求ab值.
①a﹣b=1,则a=b+1,
由已知得b+1+b=10
解得 b=![]() ,
,
a=b+l=![]() +1=
+1=![]()
则ab=![]() =
=![]()
②a﹣b=﹣1,即b﹣a=1,由①可得,b=![]() ,a=
,a=![]()
则ab=![]() =
=![]() .
.
探究三:当a﹣b=±2时,求ab值(仿照上述方法,写出探究过程).
探究四:完成下表:
a﹣b | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
ab | … |
|
|
| 25 |
|
|
| … |
(结论)若a+b=10,则ab的最大值是 (观察上面表格,直接写出结果).
(拓展)若a+b=m,则ab的最大值是 .
(应用)用一根长为12m的铁丝围成一个长方形,这个长方形面积的最大值是 m2.
查看答案和解析>>
科目:初中数学 来源: 题型:
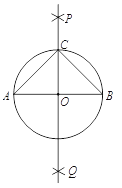
【题目】下面是“作以已知线段为斜边的等腰直角三角形”的尺规作图过程.
已知:线段![]() .
.
![]()
求作:以![]() 为斜边的一个等腰直角三角形
为斜边的一个等腰直角三角形![]() .
.
作法:如图,
(1)分别以点![]() 和点
和点![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧相交于
的长为半径作弧,两弧相交于![]() ,
,![]() 两点;
两点;
(2)作直线![]() ,交
,交![]() 于点
于点![]() ;
;
(3)以![]() 为圆心,
为圆心,![]() 的长为半径作圆,交直线
的长为半径作圆,交直线![]() 于点
于点![]() ;
;
(4)连接![]() ,
,![]() .
.
则![]() 即为所求作的三角形.
即为所求作的三角形.
请回答:在上面的作图过程中,①![]() 是直角三角形的依据是________;②
是直角三角形的依据是________;②![]() 是等腰三角形的依据是__________.
是等腰三角形的依据是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上的A、B、C三点所表示的数分别为a、b、1,且|a﹣1|+|b﹣1|=|a﹣b|,则下列选项中,满足A、B、C三点位置关系的数轴为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() :
:![]() 交
交![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 点
点![]() .
.
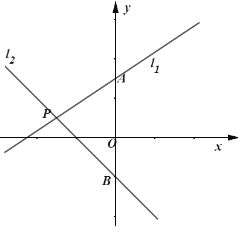
(1)求直线![]() 的函数解析式;
的函数解析式;
(2)过动点![]() 作
作![]() 轴的垂线与直线
轴的垂线与直线![]() 、
、![]() 分别交于
分别交于![]() 、
、![]() 两点,且
两点,且![]() .
.
①求![]() 的取值范围;
的取值范围;
②若![]() ,直接写出
,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲、乙两校40名学生成绩的频数分布统计表如下:
成绩x 学校 |
|
|
|
|
|
甲 | 4 | 11 | 13 | 10 | 2 |
乙 | 6 | 3 | 15 | 14 | 2 |
(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)
b.甲校成绩在![]() 这一组的是:
这一组的是:
70 70 70 71 72 73 73 73 74 75 76 77 78
c.甲、乙两校成绩的平均分、中位数、众数如下:
学校 | 平均分 | 中位数 | 众数 |
甲 | 74.2 | n | 5 |
乙 | 73.5 | 76 | 84 |
根据以上信息,回答下列问题:
(1)写出表中n的值;
(2)在此次测试中,某学生的成绩是74分,在他所属学校排在前20名,由表中数据可知该学生是_____________校的学生(填“甲”或“乙”),理由是__________;
(3)假设乙校800名学生都参加此次测试,估计成绩优秀的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com