
【题目】(问题)若a+b=10,则ab的最大值是多少?
(探究)
探究一:当a﹣b=0时,求ab值.
显然此时,a=b=5,则ab=5×5=25
探究二:当a﹣b=±1时,求ab值.
①a﹣b=1,则a=b+1,
由已知得b+1+b=10
解得 b=![]() ,
,
a=b+l=![]() +1=
+1=![]()
则ab=![]() =
=![]()
②a﹣b=﹣1,即b﹣a=1,由①可得,b=![]() ,a=
,a=![]()
则ab=![]() =
=![]() .
.
探究三:当a﹣b=±2时,求ab值(仿照上述方法,写出探究过程).
探究四:完成下表:
a﹣b | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
ab | … |
|
|
| 25 |
|
|
| … |
(结论)若a+b=10,则ab的最大值是 (观察上面表格,直接写出结果).
(拓展)若a+b=m,则ab的最大值是 .
(应用)用一根长为12m的铁丝围成一个长方形,这个长方形面积的最大值是 m2.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:
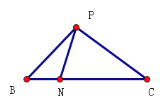
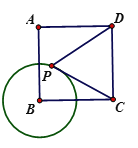
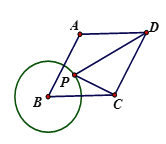
图1 图2 图3
(1)初步思考:
如图1, 在![]() 中,已知
中,已知![]() ,BC=4,N为BC上一点且
,BC=4,N为BC上一点且![]() ,试说明:
,试说明:![]()
(2)问题提出:
如图2,已知正方形ABCD的边长为4,圆B的半径为2,点P是圆B上的一个动点,求![]() 的最小值.
的最小值.
(3)推广运用:
如图3,已知菱形ABCD的边长为4,∠B﹦60°,圆B的半径为2,点P是圆B上的一个动点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆圆O的直径,C是弧AB的中点,M是弦AC的中点,CH⊥BM,垂足为H.求证
(1)∠AHO=90°
(2)求证:CH=AHOH.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(x1,y1)、B(x2,y2)在二次函数y=x2+mx+n的图像上,当x1=1、x2=3时,y1=y2.
(1)若P(a,b1),Q(3,b2)是函数图象上的两点,b1>b2,则实数a的取值范围是( )
A.a<1 B.a>3 C.a<1或a>3 D.1<a<3
(2)若抛物线与x轴只有一个公共点,求二次函数的表达式.
(3)若对于任意实数x1、x2都有y1+y2≥2,则n的范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郑奶奶提着篮子去农贸市场买鸡蛋,摊主按郑奶奶的要求,用电子秤称了5千克鸡蛋,郑奶奶怀疑重量不对,把鸡蛋放入自带的质量为0.6千克的篮子中(篮子质量准确),要求放在电子秤上再称一遍,称得为5.75千克,老板客气地说:“除去篮子后为5.15千克,老顾客啦,多0.15千克就算了”,郑奶奶高兴地付了钱,满意地回家了。以下说法正确的是( )

A.郑奶奶赚了,鸡蛋的实际质量为5.15千克
B.郑奶奶亏了,鸡蛋的实际质量为4千克
C.郑奶奶亏了,鸡蛋的实际质量为4.85千克
D.郑奶奶不亏也不赚,鸡蛋的实际质量为5千克
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P(2,﹣3)在抛物线L:y=ax2﹣2ax+a+k(a,k均为常数且a≠0)上,L交y轴于点C,连接CP.
(1)用a表示k,并求L的对称轴;
(2)当L经过点(4,﹣7)时,求此时L的表达式及其顶点坐标;
(3)横,纵坐标都是整数的点叫做整点.如图,当a<0时,若L在点C,P之间的部分与线段CP所围成的区域内(不含边界)恰有5个整点,求a的取值范围;
(4)点M(x1,y1),N(x2,y2)是L上的两点,若t≤x1≤t+1,当x2≥3时,均有y1≥y2,直接写出t的取值范围.
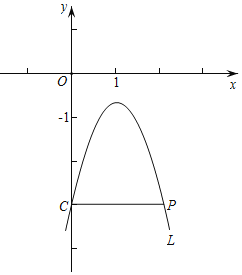
查看答案和解析>>
科目:初中数学 来源: 题型:
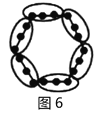
【题目】“分块计数法”:对有规律的图形进行计数时,有些题可以采用“分块计数”的方法.
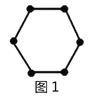
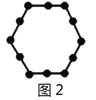
例如:图1有6个点,图2有12个点,图3有18个点,…,按此规律,求图8、图![]() 有多少个点?
有多少个点?
我们将每个图形分成完全相同的6块,每块黑点的个数相同(如图),这样图1中黑点个数是![]() 个;图2中黑点个数是
个;图2中黑点个数是![]() 个;图3中黑点个数是
个;图3中黑点个数是![]() 个;…,所以容易求出图8、图
个;…,所以容易求出图8、图![]() 中黑点的个数分别是______、_________.
中黑点的个数分别是______、_________.

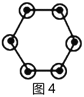
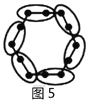
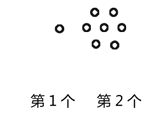
请你参考以上“分块计数法”,先将下面的点阵进行分块(画在答题卡上),再完成以下问题:
(1)第6个点阵中有______个圆圈;第![]() 个点阵中有______个圆圈.
个点阵中有______个圆圈.
(2)小圆圈的个数会等于331吗?请求出是第几个点阵.


查看答案和解析>>
科目:初中数学 来源: 题型:
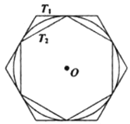
【题目】如图,有一个圆![]() 和两个正六边形
和两个正六边形![]() ,
,![]() .
.![]() 的6个顶点都在圆周上,
的6个顶点都在圆周上,![]() 的6条边都和圆
的6条边都和圆![]() 相切(我们称
相切(我们称![]() ,
,![]() 分别为圆
分别为圆![]() 的外切正六边形和内接正六边形),若设
的外切正六边形和内接正六边形),若设![]() ,
,![]() 的周长分别为
的周长分别为![]() ,
,![]() ,圆
,圆![]() 的半径为
的半径为![]() ,则
,则![]() ___;
___;![]() ____;正六边形
____;正六边形![]() ,
,![]() 的面积比
的面积比![]() 的值是____.
的值是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
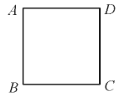
【题目】数学课上,王老师让同学们对给定的正方形![]() ,建立合适的平面直角坐标系,并表示出各顶点的坐标.下面是4名同学表示各顶点坐标的结果:
,建立合适的平面直角坐标系,并表示出各顶点的坐标.下面是4名同学表示各顶点坐标的结果:
甲同学:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
乙同学:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
丙同学:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
丁同学:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
上述四名同学表示的结果中,四个点的坐标都表示正确的同学是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com