
【题目】在滑草过程中,小明发现滑道两边形如两条双曲线,如图,点A1,A2,A3…在反比例函数y=![]() (x>0)的图象上,点B1,B2,B3…反比例函数y=
(x>0)的图象上,点B1,B2,B3…反比例函数y=![]() (k>1,x>0)的图象上,A1B1∥A2B2…∥y轴,已知点A1,A2…的横坐标分别为1,2,…,令四边形A1B1B2A2、A2B2B3A3、…的面积分别为S1、S2、…
(k>1,x>0)的图象上,A1B1∥A2B2…∥y轴,已知点A1,A2…的横坐标分别为1,2,…,令四边形A1B1B2A2、A2B2B3A3、…的面积分别为S1、S2、…
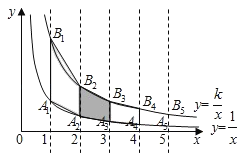
(1)用含k的代数式表示S1=_____.
(2)若S19=39,则k=_____.
【答案】![]() 761
761
【解析】
(1)根据反比例函数图象上点的特征和平行于y轴的直线的性质计算A1B1、A2B2、…,最后根据梯形面积公式可得S1的面积;
(2)分别计算S2、S3、…Sn的值并找规律,根据已知S19=39列方程可得k的值.
解:(1)∵A1B1∥A2B2…∥y轴,
∴A1和B1的横坐标相等,A2和B2的横坐标相等,…,An和Bn的横坐标相等,
∵点A1,A2…的横坐标分别为1,2,…,
∴点B1,B2…的横坐标分别为1,2,…,
∵点A1,A2,A3…在反比例函数y=![]() (x>0)的图象上,点B1,B2,B3…反比例函数y=
(x>0)的图象上,点B1,B2,B3…反比例函数y=![]() (k>1,x>0)的图象上,
(k>1,x>0)的图象上,
∴A1B1=k﹣1,A2B2=![]() ,
,
∴S1=![]() ×1×(
×1×(![]() +k﹣1)=
+k﹣1)=![]() (
(![]() k﹣
k﹣![]() )=
)=![]() ,
,
故答案为:![]() ;
;
(2)由(1)同理得:A3B3=![]() ﹣
﹣![]() =
=![]() ,A4B4=
,A4B4=![]() ,…,
,…,
∴S2=![]() [
[![]() +
+![]() (k﹣1)]=
(k﹣1)]=![]() (k﹣1),
(k﹣1),
S3=![]() [
[![]() ]=
]=![]() …,
…,
∴Sn=![]() ,
,
∵S19=39,
∴![]() ×(k﹣1)=39,
×(k﹣1)=39,
解得:k=761,
故答案为:761.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:
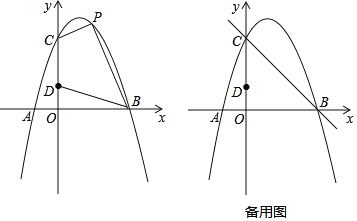
【题目】如图,对称轴为直线![]() 的抛物线经过
的抛物线经过![]() 、
、![]() 两点,与
两点,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,点
,点![]() 在
在![]() 轴上,且
轴上,且![]() .
.
(1)求该抛物线的表达式;
(2)设该抛物线上的一个动点![]() 的横坐标为
的横坐标为![]() .
.
①当![]() 时,求四边形
时,求四边形![]() 的面积
的面积![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值;
的最大值;
②点![]() 在直线
在直线![]() 上,若以
上,若以![]() 为边,点
为边,点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,请求出所有符合条件的点
为顶点的四边形是平行四边形,请求出所有符合条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
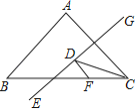
【题目】如图,等腰△ABC的底边BC=20,面积为120,点F在边BC上,且BF=3FC,EG是腰AC的垂直平分线,若点D在EG上运动,则△CDF周长的最小值为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
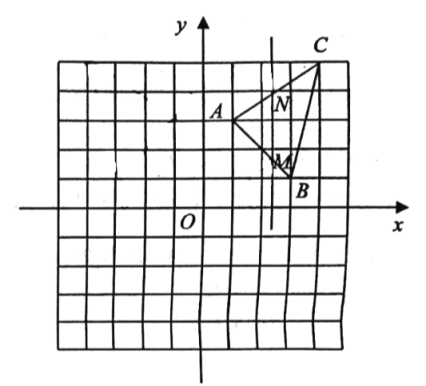
【题目】如图,在平面直角坐标系中,点![]() ,点
,点![]() ,点
,点![]() .
.
(1)画出![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() ,并写出点
,并写出点![]() 的对称点
的对称点![]() 的坐标;
的坐标;
(2)若点![]() 在
在![]() 轴上,连接
轴上,连接![]() 、
、![]() ,则
,则![]() 的最小值是 ;
的最小值是 ;
(3)若直线![]() 轴,与线段
轴,与线段![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() (点
(点![]() 不与点
不与点![]() 重合),若将
重合),若将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 的对称点为点
的对称点为点![]() ,当点
,当点![]() 落在
落在![]() 的内部(包含边界)时,点
的内部(包含边界)时,点 的横坐标
的横坐标![]() 的取值范围是 .
的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆圆O的直径,C是弧AB的中点,M是弦AC的中点,CH⊥BM,垂足为H.求证
(1)∠AHO=90°
(2)求证:CH=AHOH.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织数学兴趣探究活动,爱思考的小实同学在探究两条直线的位置关系查阅资料时发现,两条中线互相垂直的三角形称为“中垂三角形”.如图1、图2、图3中,AF、BE是△ABC的中线,AF⊥BE于点P,像△ABC这样的三角形均称为“中垂三角形”.
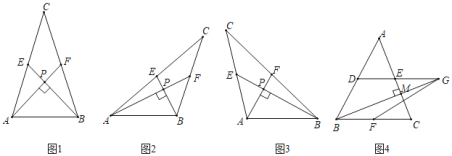
(1)如图1,当∠PAB=45°,AB=6![]() 时,AC= ,BC= ;如图2,当sin∠PAB=
时,AC= ,BC= ;如图2,当sin∠PAB=![]() ,AB=4时,AC= ,BC= ;
,AB=4时,AC= ,BC= ;
(2)请你观察(1)中的计算结果,猜想AB2、BC2、AC2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
(3)如图4,在△ABC中,AB=4![]() ,BC=2
,BC=2![]() ,D、E、F分别是边AB、AC、BC的中点,连结DE并延长至G,使得GE=DE,连结BG,当BG⊥AC于点M时,求GF的长.
,D、E、F分别是边AB、AC、BC的中点,连结DE并延长至G,使得GE=DE,连结BG,当BG⊥AC于点M时,求GF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(x1,y1)、B(x2,y2)在二次函数y=x2+mx+n的图像上,当x1=1、x2=3时,y1=y2.
(1)若P(a,b1),Q(3,b2)是函数图象上的两点,b1>b2,则实数a的取值范围是( )
A.a<1 B.a>3 C.a<1或a>3 D.1<a<3
(2)若抛物线与x轴只有一个公共点,求二次函数的表达式.
(3)若对于任意实数x1、x2都有y1+y2≥2,则n的范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P(2,﹣3)在抛物线L:y=ax2﹣2ax+a+k(a,k均为常数且a≠0)上,L交y轴于点C,连接CP.
(1)用a表示k,并求L的对称轴;
(2)当L经过点(4,﹣7)时,求此时L的表达式及其顶点坐标;
(3)横,纵坐标都是整数的点叫做整点.如图,当a<0时,若L在点C,P之间的部分与线段CP所围成的区域内(不含边界)恰有5个整点,求a的取值范围;
(4)点M(x1,y1),N(x2,y2)是L上的两点,若t≤x1≤t+1,当x2≥3时,均有y1≥y2,直接写出t的取值范围.
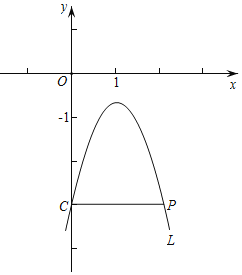
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 两点,与
两点,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,点
,点![]() 是第一象限抛物线上的点,连结
是第一象限抛物线上的点,连结![]() 交直线
交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐为
的横坐为![]() ,
,![]() 与
与![]() 的比值为
的比值为![]() .
.
(1)![]() __________;
__________;
(2)当![]() 取最大值时,
取最大值时,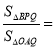 __________.
__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com