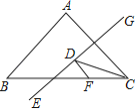
【题目】如图，等腰△ABC的底边BC=20，面积为120，点F在边BC上，且BF=3FC，EG是腰AC的垂直平分线，若点D在EG上运动，则△CDF周长的最小值为__．
芝麻开花课程新体验系列答案科目：初中数学 来源： 题型：
【题目】如图，已知二次函数
的图象经过点
．
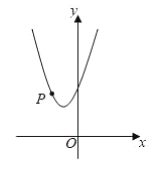
（1）求
的值和图象的顶点坐标；
（2）点
在该二次函数图象上．
①当
时，求
的值；
②若点
到
轴的距离小于2，请根据图象直接写出的取值范围；
③直接写出点与直线
的距离小于
时
的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为落实疫情期间的垃圾分类，树立全面环保意识，某校举行了“垃圾分类，绿色环保”知识竞赛活动，根据学生的成绩划分为
，
，
，
四个等级，并绘制了不完整的两种统计图：
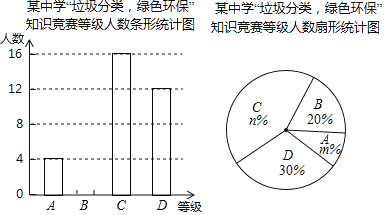
根据图中提供的信息，回答下列问题：
（1）参加知识竞赛的学生共有______人，并把条形统计图补充完整；
（2）扇形统计图中，
______，
______，等级对应的圆心角为______度；
（3）小明是四名获等级的学生中的一位，学校将从获等级的学生中任选取2人，参加市举办的知识竞赛，请用列表法或画树状图，求小明被选中参加区知识竞赛的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
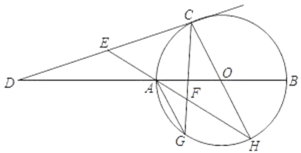
【题目】如图，已知AB为⊙O的直径，C为⊙O上异于A、B的一点，过C点的切线与BA的延长线交于D点，E为CD上一点，连接EA并延长交⊙O于H，F为EH上一点，且EF＝CE，CF交延长线交⊙O于G．
（1）求证：弧AG＝弧GH；
（2）若E为DC的中点，sim∠CDO＝
，AH＝2
，求⊙O的半径．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】快递公司为提高快递分拣的速度，决定购买机器人来代替人工分拣，两种型号的机器人的工作效率和价格如表：
型号 | 甲 | 乙 |
每台每小时分拣快递件数(件) | 1000 | 800 |
每台价格(万元) | 5 | 3 |
该公司计划购买这两种型号的机器人共10台，并且使这10台机器人每小时分拣快递件数总和不少于8500件
(1)设购买甲种型号的机器人x台，购买这10台机器人所花的费用为y万元，求y与x之间的关系式；
(2)购买几台甲种型号的机器人，能使购买这10台机器人所花总费用最少？最少费用是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
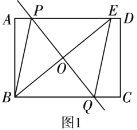
【题目】（1）如图1，矩形
中，点
、
分别在线段
、
上，点
与点
关于
对称，点在线段上，连接
、
、交
于点
．求证：四边形
是菱形；
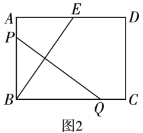
（2）如图2，矩形中，
，点、分别在线段
、上，点与点关于对称，点在线段上，
，求
的长；
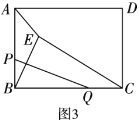
（3）如图3，有一块矩形空地，
，
，点是一个休息站且在线段上，
，点在线段上，现要在点关于对称的点处修建一口水井，并且修建水渠
和
，以便于在四边形空地
上种植花草，余下部分贴上地砖．种植花草的四边形空地的面积是否存在最小值，若存在，请求出最小值，若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
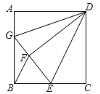
【题目】如图，已知正方形ABCD的边长为6，BE=EC，将正方形边CD沿DE折叠到DF，延长EF交AB于G，连接DG，现在有如下4个结论：①
；②
；③
；④
在以上4个结论中，正确的有（ ）
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在滑草过程中，小明发现滑道两边形如两条双曲线，如图，点A1，A2，A3…在反比例函数y＝
（x＞0）的图象上，点B1，B2，B3…反比例函数y＝
（k＞1，x＞0）的图象上，A1B1∥A2B2…∥y轴，已知点A1，A2…的横坐标分别为1，2，…，令四边形A1B1B2A2、A2B2B3A3、…的面积分别为S1、S2、…
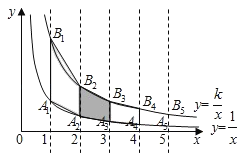
（1）用含k的代数式表示S1＝_____．
（2）若S19＝39，则k＝_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】数轴上的A、B、C三点所表示的数分别为a、b、1，且|a﹣1|+|b﹣1|＝|a﹣b|，则下列选项中，满足A、B、C三点位置关系的数轴为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
