
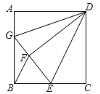
【题目】如图,已知正方形ABCD的边长为6,BE=EC,将正方形边CD沿DE折叠到DF,延长EF交AB于G,连接DG,现在有如下4个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 在以上4个结论中,正确的有( )
在以上4个结论中,正确的有( )
A. 1B. 2C. 3D. 4
【答案】C
【解析】
根据正方形的性质和折叠的性质可得AD=DF,∠A=∠GFD=90°,于是根据“HL”判定△ADG≌△FDG,再由GF+GB=GA+GB=12,EB=EF,△BGE为直角三角形,可通过勾股定理列方程求出AG=4,BG=8,进而求出△BEF的面积,再抓住△BEF是等腰三角形,而△GED显然不是等腰三角形,判断③是错误的.
解:由折叠可知,DF=DC=DA,∠DFE=∠C=90,
∴∠DFG=∠A=90,
在Rt△ADG与Rt△FDG中![]()
∴Rt△ADG≌Rt△FDG(HL),故①正确;
∵正方形边长为6,
∴BE=EC=EF=3,
设AG=FG=x,则EG=x+3,BG=6x,
由勾股定理得:![]() ,
,
即:![]() ,
,
解得:![]() ;
;
∴AG=GF=2,BG=4,BG=2AG,故②正确;
BE=EF=3,△BEF是等腰三角形,易知△GED不是等腰三角形,故③错误;
S△GBE=![]() ,
,![]() ,S△BEF
,S△BEF![]() ,故④正确。
,故④正确。
故正确的有①②④,选C.


科目:初中数学 来源: 题型:
【题目】某校开设了“3D”打印、数学史、诗歌欣赏、陶艺制作四门校本课程,为了解学生对这四门校本课程的喜爱情况,对学生进行了随机问卷调查(问卷调查表如图所示),将调查结果整理后绘制了(图1)、(图2)两幅均不完整的统计图.
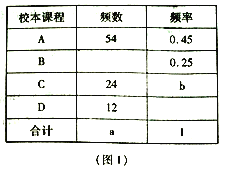
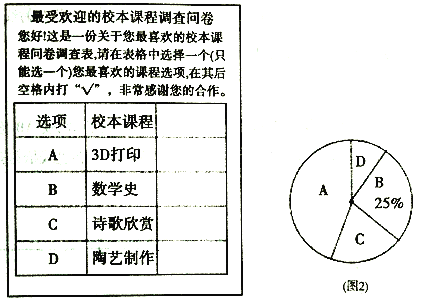
请您根据图中提供的信息回答下列问题:
(1)统计图中的a= ,b= ;
(2)“D”对应扇形的圆心角为 度;
(3)根据调查结果,请您估计该校1200名学生中最喜欢“数学史”校本课程的人数;
(4)小明和小亮参加校本课程学习,若每人从“A”、“B”、“C”三门校本课程中随机选取一门,请用画树状图或列表格的方法,求两人恰好选中同一门校本课程的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:
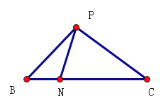
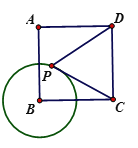
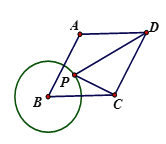
图1 图2 图3
(1)初步思考:
如图1, 在![]() 中,已知
中,已知![]() ,BC=4,N为BC上一点且
,BC=4,N为BC上一点且![]() ,试说明:
,试说明:![]()
(2)问题提出:
如图2,已知正方形ABCD的边长为4,圆B的半径为2,点P是圆B上的一个动点,求![]() 的最小值.
的最小值.
(3)推广运用:
如图3,已知菱形ABCD的边长为4,∠B﹦60°,圆B的半径为2,点P是圆B上的一个动点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
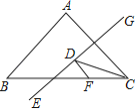
【题目】如图,等腰△ABC的底边BC=20,面积为120,点F在边BC上,且BF=3FC,EG是腰AC的垂直平分线,若点D在EG上运动,则△CDF周长的最小值为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
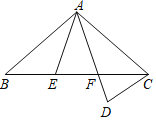
【题目】如图,△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.
(1)求证:△ABE≌△ACF;
(2)若∠BAE=30°,则∠ADC= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
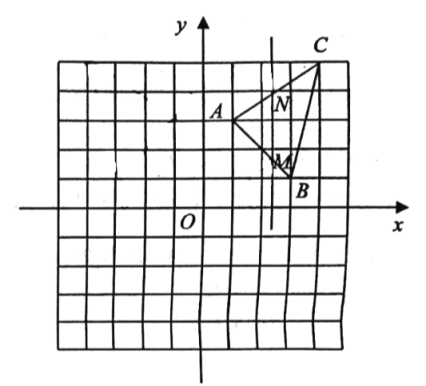
【题目】如图,在平面直角坐标系中,点![]() ,点
,点![]() ,点
,点![]() .
.
(1)画出![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() ,并写出点
,并写出点![]() 的对称点
的对称点![]() 的坐标;
的坐标;
(2)若点![]() 在
在![]() 轴上,连接
轴上,连接![]() 、
、![]() ,则
,则![]() 的最小值是 ;
的最小值是 ;
(3)若直线![]() 轴,与线段
轴,与线段![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() (点
(点![]() 不与点
不与点![]() 重合),若将
重合),若将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 的对称点为点
的对称点为点![]() ,当点
,当点![]() 落在
落在![]() 的内部(包含边界)时,点
的内部(包含边界)时,点 的横坐标
的横坐标![]() 的取值范围是 .
的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆圆O的直径,C是弧AB的中点,M是弦AC的中点,CH⊥BM,垂足为H.求证
(1)∠AHO=90°
(2)求证:CH=AHOH.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(x1,y1)、B(x2,y2)在二次函数y=x2+mx+n的图像上,当x1=1、x2=3时,y1=y2.
(1)若P(a,b1),Q(3,b2)是函数图象上的两点,b1>b2,则实数a的取值范围是( )
A.a<1 B.a>3 C.a<1或a>3 D.1<a<3
(2)若抛物线与x轴只有一个公共点,求二次函数的表达式.
(3)若对于任意实数x1、x2都有y1+y2≥2,则n的范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
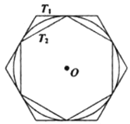
【题目】如图,有一个圆![]() 和两个正六边形
和两个正六边形![]() ,
,![]() .
.![]() 的6个顶点都在圆周上,
的6个顶点都在圆周上,![]() 的6条边都和圆
的6条边都和圆![]() 相切(我们称
相切(我们称![]() ,
,![]() 分别为圆
分别为圆![]() 的外切正六边形和内接正六边形),若设
的外切正六边形和内接正六边形),若设![]() ,
,![]() 的周长分别为
的周长分别为![]() ,
,![]() ,圆
,圆![]() 的半径为
的半径为![]() ,则
,则![]() ___;
___;![]() ____;正六边形
____;正六边形![]() ,
,![]() 的面积比
的面积比![]() 的值是____.
的值是____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com