
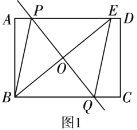
【题目】(1)如图1,矩形![]() 中,点
中,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上,点
上,点![]() 与点
与点![]() 关于
关于![]() 对称,点
对称,点![]() 在线段
在线段![]() 上,连接
上,连接![]() 、
、![]() 、
、![]() 交
交![]() 于点
于点![]() .求证:四边形
.求证:四边形![]() 是菱形;
是菱形;
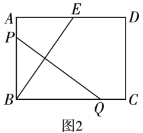
(2)如图2,矩形![]() 中,
中,![]() ,点
,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上,点
上,点![]() 与点
与点![]() 关于
关于![]() 对称,点
对称,点![]() 在线段
在线段![]() 上,
上,![]() ,求
,求![]() 的长;
的长;
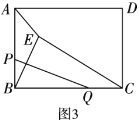
(3)如图3,有一块矩形空地![]() ,
,![]() ,
,![]() ,点
,点![]() 是一个休息站且在线段
是一个休息站且在线段![]() 上,
上,![]() ,点
,点![]() 在线段
在线段![]() 上,现要在点
上,现要在点![]() 关于
关于![]() 对称的点
对称的点![]() 处修建一口水井,并且修建水渠
处修建一口水井,并且修建水渠![]() 和
和![]() ,以便于在四边形空地
,以便于在四边形空地![]() 上种植花草,余下部分贴上地砖.种植花草的四边形空地
上种植花草,余下部分贴上地砖.种植花草的四边形空地![]() 的面积是否存在最小值,若存在,请求出最小值,若不存在,请说明理由.
的面积是否存在最小值,若存在,请求出最小值,若不存在,请说明理由.
【答案】(1)见解析;(2)![]() ;(3)3000.
;(3)3000.
【解析】
(1)先证![]() ,证明四边形
,证明四边形![]() 是平行四边形,再根据
是平行四边形,再根据![]() 即可证明是菱形;
即可证明是菱形;
(2)连接![]() ,设
,设![]() ,在Rt△APE中,根据勾股定理解出x即可;
,在Rt△APE中,根据勾股定理解出x即可;
(3)先表示出四边形的面积得到![]() 最小时,四边形
最小时,四边形![]() 的面积最小,当点
的面积最小,当点![]() ,
,![]() ,
,![]() 在同一条线上时,
在同一条线上时,![]() 最小,再证
最小,再证![]() ,根据相似比求出EG,从而求出面积的最小值.
,根据相似比求出EG,从而求出面积的最小值.
解:(1)证明:由对称可知:![]() ,
,
在矩形![]() 中,
中,![]() ,
,
∴![]() ,
,
在 △POE和△QOB中,

∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∵点![]() 与点
与点![]() 关于
关于![]() 对称,
对称,
∴![]() ,
,
∴四边形![]() 是菱形;
是菱形;
(2)连接![]() ,由对称知,
,由对称知,![]() ,
,
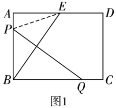
设![]() ,
,
∴![]() ,
,
在Rt△APE中,根据勾股定理得,![]() 即
即![]() ,
,
∴解得:![]() ,
,
∴![]() ;
;
(3)连接![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
连接![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,
,

∴![]() 四边形
四边形![]()
![]()
![]()
![]() ,
,
∴![]() 最小时,四边形
最小时,四边形![]() 的面积最小,
的面积最小,
对称可知,![]() ,
,
∴点![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的一段弧上的一点,
为半径的一段弧上的一点,
∴点![]() ,
,![]() ,
,![]() 在同一条线上时,
在同一条线上时,![]() 最小,
最小,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() 最小
最小![]() ,
,
∴四边形![]() 的面积最小值S
的面积最小值S![]()
![]() .
.


科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②3a+c=0;③4a+2b+c<0;④若(-5,y1),(![]() ,y2)是抛物线上两点,则y1> y2.其中说法正确的是( )
,y2)是抛物线上两点,则y1> y2.其中说法正确的是( )
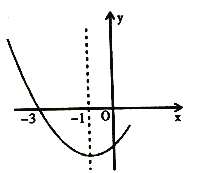
A.①②B.②③C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
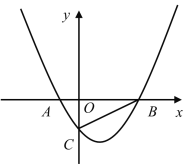
【题目】如图,已知二次函数![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(
两点(![]() 点在
点在![]() 点左),与
点左),与![]() 轴交于
轴交于![]() 点,连接
点,连接![]() ,点
,点![]() 为二次函数图象上的动点.
为二次函数图象上的动点.
(1)若![]() 的面积为3,求抛物线的解析式;
的面积为3,求抛物线的解析式;
(2)在(1)的条件下,若在![]() 轴上存在点
轴上存在点![]() ,使得
,使得![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若![]() 为对称轴右侧抛物线上的动点,直线
为对称轴右侧抛物线上的动点,直线![]() 交
交![]() 轴于
轴于![]() 点,直线
点,直线![]() 交
交![]() 轴于点
轴于点![]() ,判断
,判断![]() 的值是否为定值,若是,求出定值,若不是请说明理由.
的值是否为定值,若是,求出定值,若不是请说明理由.
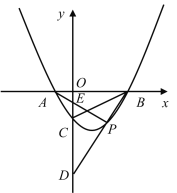
查看答案和解析>>
科目:初中数学 来源: 题型:
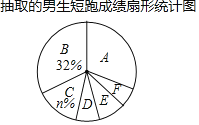
【题目】中国飞人苏炳添以6秒47获得2019年国际田联伯明翰室内赛男子60米冠军,苏炳添夺冠掀起跑步热潮某校为了解该校八年级男生的短跑水平,全校八年级男生中随机抽取了部分男生,对他们的短跑水平进行测试,并将测试成绩(满分10分)绘制成如下不完整的统计图表:
组别 | 成绩/分 | 人数/人 |
A | 5 | 36 |
B | 6 | 32 |
C | 7 | 15 |
D | 8 | 8 |
E | 9 | 5 |
F | 10 | m |
请你根据统计图表中的信息,解答下列问题:
(1)填空:m=_____,n=_____;
(2)所抽取的八年级男生短跑成绩的众数是_____分,扇形统计图中E组的扇形圆心角的度数为____°;
(3)求所抽取的八年级男生短跑的平均成绩.
查看答案和解析>>
科目:初中数学 来源: 题型:
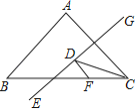
【题目】如图,等腰△ABC的底边BC=20,面积为120,点F在边BC上,且BF=3FC,EG是腰AC的垂直平分线,若点D在EG上运动,则△CDF周长的最小值为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() .
.
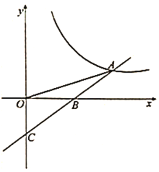
(1)求反比例函数与一次函数的表达式;
(2)若点![]() 为x轴上一点,
为x轴上一点,![]() 是等腰三角形,求点
是等腰三角形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
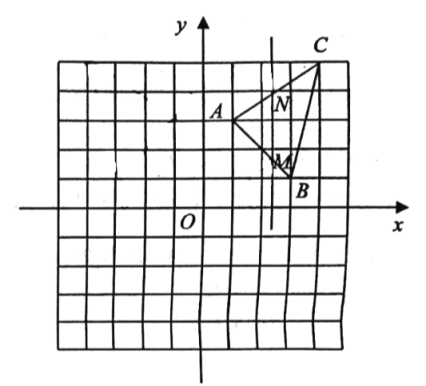
【题目】如图,在平面直角坐标系中,点![]() ,点
,点![]() ,点
,点![]() .
.
(1)画出![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() ,并写出点
,并写出点![]() 的对称点
的对称点![]() 的坐标;
的坐标;
(2)若点![]() 在
在![]() 轴上,连接
轴上,连接![]() 、
、![]() ,则
,则![]() 的最小值是 ;
的最小值是 ;
(3)若直线![]() 轴,与线段
轴,与线段![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() (点
(点![]() 不与点
不与点![]() 重合),若将
重合),若将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 的对称点为点
的对称点为点![]() ,当点
,当点![]() 落在
落在![]() 的内部(包含边界)时,点
的内部(包含边界)时,点 的横坐标
的横坐标![]() 的取值范围是 .
的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织数学兴趣探究活动,爱思考的小实同学在探究两条直线的位置关系查阅资料时发现,两条中线互相垂直的三角形称为“中垂三角形”.如图1、图2、图3中,AF、BE是△ABC的中线,AF⊥BE于点P,像△ABC这样的三角形均称为“中垂三角形”.
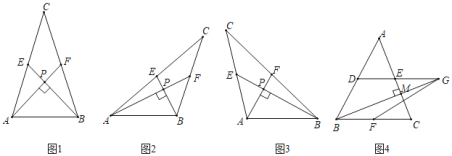
(1)如图1,当∠PAB=45°,AB=6![]() 时,AC= ,BC= ;如图2,当sin∠PAB=
时,AC= ,BC= ;如图2,当sin∠PAB=![]() ,AB=4时,AC= ,BC= ;
,AB=4时,AC= ,BC= ;
(2)请你观察(1)中的计算结果,猜想AB2、BC2、AC2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
(3)如图4,在△ABC中,AB=4![]() ,BC=2
,BC=2![]() ,D、E、F分别是边AB、AC、BC的中点,连结DE并延长至G,使得GE=DE,连结BG,当BG⊥AC于点M时,求GF的长.
,D、E、F分别是边AB、AC、BC的中点,连结DE并延长至G,使得GE=DE,连结BG,当BG⊥AC于点M时,求GF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
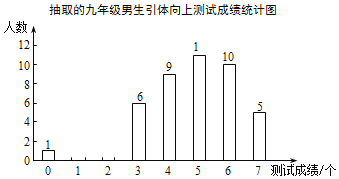
【题目】某中学九年级男生共250人,现随机抽取了部分九年级男生进行引体向上测试,相关数据的统计图如下.设学生引体向上测试成绩为x(单位:个).学校规定:当0≤x<2时成绩等级为不及格,当2≤x<4时成绩等级为及格,当4≤x<6时成绩等级为良好,当x≥6时成绩等级为优秀.样本中引体向上成绩优秀的人数占30%,成绩为1个和2个的人数相同.
(1)补全统计图;
(2)估计全校九年级男生引体向上测试不及格的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com