
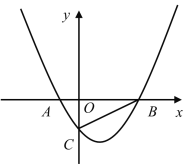
【题目】如图,已知二次函数![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(
两点(![]() 点在
点在![]() 点左),与
点左),与![]() 轴交于
轴交于![]() 点,连接
点,连接![]() ,点
,点![]() 为二次函数图象上的动点.
为二次函数图象上的动点.
(1)若![]() 的面积为3,求抛物线的解析式;
的面积为3,求抛物线的解析式;
(2)在(1)的条件下,若在![]() 轴上存在点
轴上存在点![]() ,使得
,使得![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若![]() 为对称轴右侧抛物线上的动点,直线
为对称轴右侧抛物线上的动点,直线![]() 交
交![]() 轴于
轴于![]() 点,直线
点,直线![]() 交
交![]() 轴于点
轴于点![]() ,判断
,判断![]() 的值是否为定值,若是,求出定值,若不是请说明理由.
的值是否为定值,若是,求出定值,若不是请说明理由.
【答案】(1)![]() ;(2)(-2,
;(2)(-2,![]() )或(6,
)或(6,![]() );(3)
);(3)![]() 的值为定值
的值为定值![]()
【解析】
(1)令y=0,求出点A和点B的坐标,得到AB和OC,再根据△ABC的面积求出a的值;
(2)分当点F在y轴正半轴时,当点F在y轴负半轴两种情况,过点P作y轴垂线于点Q,设点P坐标为(x,![]() ),证明△PQC∽△COB,通过比例关系求出点P的横坐标,从而得出结果;
),证明△PQC∽△COB,通过比例关系求出点P的横坐标,从而得出结果;
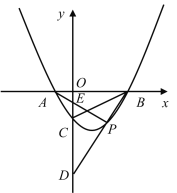
(3)设PA的解析式为:y=kx+k,PB的解析式为:y=mx-3m,分别和抛物线表达式联立,利用根与系数的关系得出点P横坐标的两种表示方法,再根据函数表达式得出点C、D、E的坐标,得到EC和DE的长,从而证明![]() 为定值.
为定值.
解:(1)令y=0,则![]() ,
,
解得:x1=-1,x2=3,
∴A(-1,0),B(3,0),
∴AB=4,OC=-3a,
∴S△ABC=![]() ,
,
解得a=![]() ,
,
∴抛物线的表达式为![]() ;
;
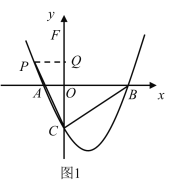
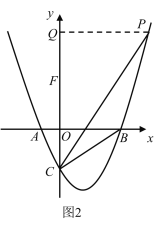
(2) 如图1、2,当点F在y轴正半轴时,
过点P作y轴垂线于点Q,
∵∠PCF=∠ABC,∠PQC=∠BOC,
∴△PQC∽△COB,
∴![]() ,
,
设点P坐标为(x,![]() ),
),
∴图1中,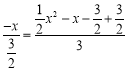 ,解得:x=-2或0(舍),
,解得:x=-2或0(舍),
图2中,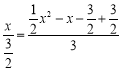 ,解得:x=6或0(舍),
,解得:x=6或0(舍),
代入抛物线表达式中可得:
点P的坐标为(-2,![]() )或(6,
)或(6,![]() );
);
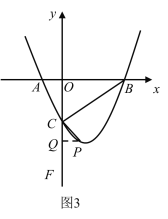
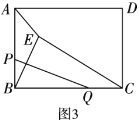
如图3,当点F在y轴负半轴时,过点P作y轴垂线于点Q,
同理可知:△PQC∽△COB,
则![]() ,设点P坐标为(x,
,设点P坐标为(x,![]() ),
),
∴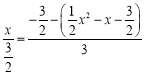 ,解得:x=-2或0,
,解得:x=-2或0,
由于此时点P只能在y轴右侧,所以x≠-2,
综上:点P的坐标为(-2,![]() )或(6,
)或(6,![]() );
);
(3)∵A(-1,0),B(3,0),
设PA的解析式为:y=kx+k,PB的解析式为:y=mx-3m,
联立:![]() ,
,![]() ,
,
可得:![]() ,
,![]() ,
,
∴点P的横坐标为![]() 或
或![]() ,且
,且![]() =
=![]() ,
,
∴m-k=4a,即k=m-4a,
E(0,k),D(0,-3m),C(0,-3a),
∴EC=k+3a,DE=k+3m,
∴![]() ,
,
故![]() 的值为定值
的值为定值![]() .
.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
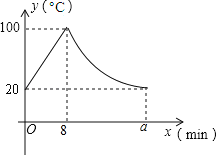
【题目】某小学为每个班级配备了一种可以加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10℃,待加热到100℃,饮水机自动停止加热,水温开始下降,水温y(℃)与通电时间x(min)成反比例关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温为20℃,接通电源后,水温y(℃)与通电时间x(min)的关系如下图所示,回答下列问题:
(1)当0≤x≤8时,求y与x之间的函数关系式;
(2)求出图中a的值;
(3)某天早上7:20,李老师将放满水后的饮水机电源打开,若他想在8:00上课前能喝到不超过40℃的温开水,问:他应在什么时间段内接水?
查看答案和解析>>
科目:初中数学 来源: 题型:
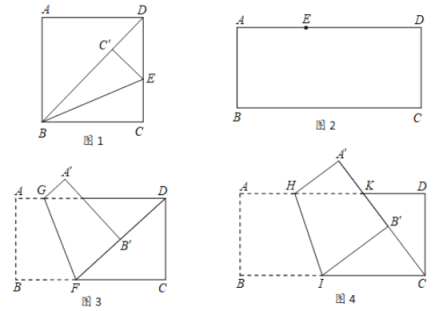
【题目】(1)如图1,将矩形ABCD折叠,使BC落在对角线BD上,折痕为BE,点C落在点C'处,若∠ADB=54°,则∠DBE的度数为 °.
(2)小明手中有一张矩形纸片ABCD,AB=4,AD=9.(画一画)如图2,点E在这张矩形纸片的边AD上,将纸片折叠,使AB落在CE所在直线上,折痕设为MN(点M,N分别在边AD,BC上),利用直尺和圆规画出折痕MN(不写作法,保留作图痕迹,并用黑色水笔把线段MN描清楚);
(3)(算一算)如图3,点F在这张矩形纸片的边BC上,将纸片折叠,使FB落在射线FD上,折痕为GF,点A,B分别落在点A',B'处,若AG=![]() ,求B'D的长;
,求B'D的长;
(4)(验一验)如图4,点K在这张矩形纸片的边AD上,DK=3,将纸片折叠,使AB落在CK所在直线上,折痕为HI,点A,B分别落在点A',B'处,小明认为B'I所在直线恰好经过点D,他的判断是否正确,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
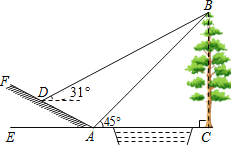
【题目】数学活动课上,小明和小红要测量小河对岸大树BC的高度,小红在点A测得大树顶端B的仰角为45°,小明从A点出发沿斜坡走3![]() 米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2.
米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2.
(1)求小明从点A到点D的过程中,他上升的高度;
(2)依据他们测量的数据能否求出大树BC的高度?若能,请计算;若不能,请说明理由.(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实疫情期间的垃圾分类,树立全面环保意识,某校举行了“垃圾分类,绿色环保”知识竞赛活动,根据学生的成绩划分为![]() ,
,![]() ,
,![]() ,
,![]() 四个等级,并绘制了不完整的两种统计图:
四个等级,并绘制了不完整的两种统计图:
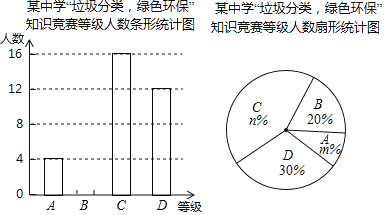
根据图中提供的信息,回答下列问题:
(1)参加知识竞赛的学生共有______人,并把条形统计图补充完整;
(2)扇形统计图中,![]() ______,
______,![]() ______,
______,![]() 等级对应的圆心角为______度;
等级对应的圆心角为______度;
(3)小明是四名获![]() 等级的学生中的一位,学校将从获
等级的学生中的一位,学校将从获![]() 等级的学生中任选取2人,参加市举办的知识竞赛,请用列表法或画树状图,求小明被选中参加区知识竞赛的概率.
等级的学生中任选取2人,参加市举办的知识竞赛,请用列表法或画树状图,求小明被选中参加区知识竞赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC 中,AB=AC,点 M 在 BA 的延长线上,点 N 在 BC 的延长线上,过点 C 作CD∥AB 交∠CAM 的平分线于点 D.
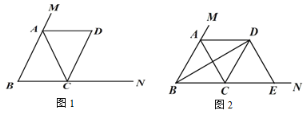
(1)如图 1,求证:四边形 ABCD 是平行四边形;
(2)如图 2,当∠ABC=60°时,连接 BD,过点 D 作 DE⊥BD,交 BN 于点 E,在不添加任何辅助线的情况下,请直接写出图 2 中四个三角形(不包含△CDE),使写出的每个三角形的面积与△CDE 的面积相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
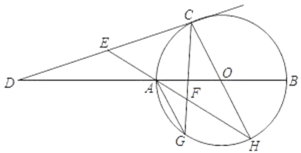
【题目】如图,已知AB为⊙O的直径,C为⊙O上异于A、B的一点,过C点的切线与BA的延长线交于D点,E为CD上一点,连接EA并延长交⊙O于H,F为EH上一点,且EF=CE,CF交延长线交⊙O于G.
(1)求证:弧AG=弧GH;
(2)若E为DC的中点,sim∠CDO=![]() ,AH=2
,AH=2![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
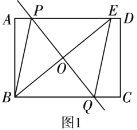
【题目】(1)如图1,矩形![]() 中,点
中,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上,点
上,点![]() 与点
与点![]() 关于
关于![]() 对称,点
对称,点![]() 在线段
在线段![]() 上,连接
上,连接![]() 、
、![]() 、
、![]() 交
交![]() 于点
于点![]() .求证:四边形
.求证:四边形![]() 是菱形;
是菱形;
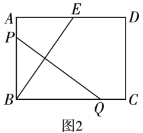
(2)如图2,矩形![]() 中,
中,![]() ,点
,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上,点
上,点![]() 与点
与点![]() 关于
关于![]() 对称,点
对称,点![]() 在线段
在线段![]() 上,
上,![]() ,求
,求![]() 的长;
的长;
(3)如图3,有一块矩形空地![]() ,
,![]() ,
,![]() ,点
,点![]() 是一个休息站且在线段
是一个休息站且在线段![]() 上,
上,![]() ,点
,点![]() 在线段
在线段![]() 上,现要在点
上,现要在点![]() 关于
关于![]() 对称的点
对称的点![]() 处修建一口水井,并且修建水渠
处修建一口水井,并且修建水渠![]() 和
和![]() ,以便于在四边形空地
,以便于在四边形空地![]() 上种植花草,余下部分贴上地砖.种植花草的四边形空地
上种植花草,余下部分贴上地砖.种植花草的四边形空地![]() 的面积是否存在最小值,若存在,请求出最小值,若不存在,请说明理由.
的面积是否存在最小值,若存在,请求出最小值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:若抛物线的顶点在坐标轴上,则称该抛物线为“数轴函数”例如抛物线y=x2和y=(x-1)2都是“数轴函数”.
(1)抛物线y=x2-4x+4和抛物线y=x2-6x是“数轴函数“吗?请说明理由;
(2)若抛物线y=2x2+4mx+m2+16是“数轴函数”,求该抛物线的表达式
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com