
【题目】在△ABC 中,AB=AC,点 M 在 BA 的延长线上,点 N 在 BC 的延长线上,过点 C 作CD∥AB 交∠CAM 的平分线于点 D.
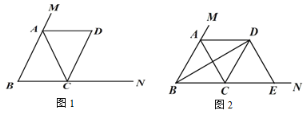
(1)如图 1,求证:四边形 ABCD 是平行四边形;
(2)如图 2,当∠ABC=60°时,连接 BD,过点 D 作 DE⊥BD,交 BN 于点 E,在不添加任何辅助线的情况下,请直接写出图 2 中四个三角形(不包含△CDE),使写出的每个三角形的面积与△CDE 的面积相等.
【答案】(1)见解析;(2)△ABC、△DBC、△ABD、△ACD.
【解析】
(1)根据等腰三角形的性质和三角形外角的性质可得∠CAM=2∠ABC,根据角平分线的定义可得∠CAM=2∠MAD,等量代换得到∠ABC=∠MAD,进而证得AD∥BC即可解决问题;
(2)首先证明平行四边形ABCD是菱形,然后证明△DCE是等边三角形,得到CE=CD=BC=AD,根据等底等高的三角形面积相等可得答案.
解:(1)∵AB=AC,
∴∠ABC=∠ACB,
∴∠CAM=∠ABC+∠ACB=2∠ABC,
∵AD是∠CAM 的平分线,
∴∠CAM=2∠MAD,
∴∠ABC=∠MAD,
∴AD∥BC,
∵CD∥AB,
∴四边形ABCD是平行四边形;
(2)∵∠ABC=60°,AB=AC,四边形ABCD是平行四边形,
∴△ABC是等边三角形,∠DCE=∠ABC=60°,
∴AB=BC,
∴平行四边形ABCD是菱形,
∴∠DBE=30°,
∵DE⊥BD,
∴∠DEB=60°,
∴△DCE是等边三角形,
∴CE=CD=BC=AD,
∵AD∥BC,
∴△ABC、△DBC、△ABD、△ACD的面积都与△CDE的面积相等.


科目:初中数学 来源: 题型:
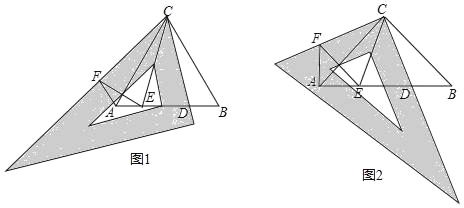
【题目】(操作发现)
(1)如图1,△ABC为等边三角形,先将三角板中的60°角与∠ACB重合,再将三角板绕点C按顺时针方向旋转(旋转角大于0°且小于30°),旋转后三角板的一直角边与AB交于点D,在三角板斜边上取一点F,使CF=CD,线段AB上取点E,使∠DCE=30°,连接AF,EF.
①求∠EAF的度数;
②DE与EF相等吗?请说明理由;
(类比探究)
(2)如图2,△ABC为等腰直角三角形,∠ACB=90°,先将三角板的90°角与∠ACB重合,再将三角板绕点C按顺时针方向旋转(旋转角大于0°且小于45°),旋转后三角板的一直角边与AB交于点D,在三角板另一直角边上取一点F,使CF=CD,线段AB上取点E,使∠DCE=45°,连接AF,EF.请直接写出探究结果:
①∠EAF的度数;
②线段AE,ED,DB之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 的四个顶点分别在矩形
的四个顶点分别在矩形![]() 的各条边上,
的各条边上,![]() ,
,![]() ,
,![]() .有以下四个结论:①
.有以下四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④矩形
;④矩形![]() 的面积是
的面积是![]() .其中正确的结论为( )
.其中正确的结论为( )
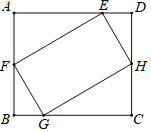
A.①②B.①②③C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
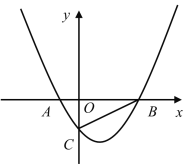
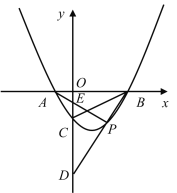
【题目】如图,已知二次函数![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(
两点(![]() 点在
点在![]() 点左),与
点左),与![]() 轴交于
轴交于![]() 点,连接
点,连接![]() ,点
,点![]() 为二次函数图象上的动点.
为二次函数图象上的动点.
(1)若![]() 的面积为3,求抛物线的解析式;
的面积为3,求抛物线的解析式;
(2)在(1)的条件下,若在![]() 轴上存在点
轴上存在点![]() ,使得
,使得![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若![]() 为对称轴右侧抛物线上的动点,直线
为对称轴右侧抛物线上的动点,直线![]() 交
交![]() 轴于
轴于![]() 点,直线
点,直线![]() 交
交![]() 轴于点
轴于点![]() ,判断
,判断![]() 的值是否为定值,若是,求出定值,若不是请说明理由.
的值是否为定值,若是,求出定值,若不是请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
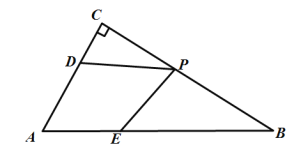
【题目】如图,在Rt△ABC中,∠C=90°,∠B=30°,点D、E分别在边AC、AB上,AD=14,点P是边BC上一动点,当PD+PE的值最小时,AE=15,则BE为( )
A.30B.29C.28D.27
查看答案和解析>>
科目:初中数学 来源: 题型:
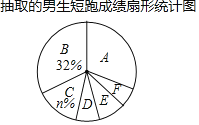
【题目】中国飞人苏炳添以6秒47获得2019年国际田联伯明翰室内赛男子60米冠军,苏炳添夺冠掀起跑步热潮某校为了解该校八年级男生的短跑水平,全校八年级男生中随机抽取了部分男生,对他们的短跑水平进行测试,并将测试成绩(满分10分)绘制成如下不完整的统计图表:
组别 | 成绩/分 | 人数/人 |
A | 5 | 36 |
B | 6 | 32 |
C | 7 | 15 |
D | 8 | 8 |
E | 9 | 5 |
F | 10 | m |
请你根据统计图表中的信息,解答下列问题:
(1)填空:m=_____,n=_____;
(2)所抽取的八年级男生短跑成绩的众数是_____分,扇形统计图中E组的扇形圆心角的度数为____°;
(3)求所抽取的八年级男生短跑的平均成绩.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() .
.
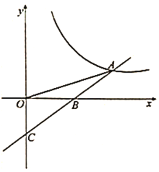
(1)求反比例函数与一次函数的表达式;
(2)若点![]() 为x轴上一点,
为x轴上一点,![]() 是等腰三角形,求点
是等腰三角形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一元二次方程ax2+bx+c=0(a≠0),下列说法:
①若b=2![]() ,则方程ax2+bx+c=0一定有两个相等的实数根;
,则方程ax2+bx+c=0一定有两个相等的实数根;
②若方程ax2+bx+c=0有两个不等的实数根,则方程x2﹣bx+ac=0也一定有两个不等的实数根;
③若c是方程ax2+bx+c=0的一个根,则一定有ac+b+1=0成立;
④若x0是一元二次方程ax2+bx+c=0的根,则b2﹣4ac=(2ax0+b)2,其中正确的( )
A.只有①②③B.只有①②④C.①②③④D.只有③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com