
ЁОЬтФПЁПЃЈВйзїЗЂЯжЃЉ
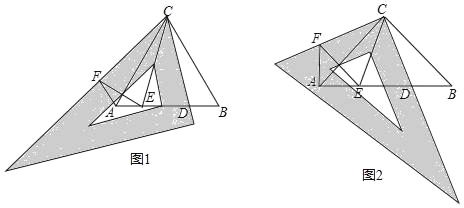
ЃЈ1ЃЉШчЭМ1ЃЌЁїABCЮЊЕШБпШ§НЧаЮЃЌЯШНЋШ§НЧАхжаЕФ60ЁуНЧгыЁЯACBжиКЯЃЌдйНЋШ§НЧАхШЦЕуCАДЫГЪБеыЗНЯђа§зЊЃЈа§зЊНЧДѓгк0ЁуЧваЁгк30ЁуЃЉЃЌа§зЊКѓШ§НЧАхЕФвЛжБНЧБпгыABНЛгкЕуDЃЌдкШ§НЧАхаББпЩЯШЁвЛЕуFЃЌЪЙCF=CDЃЌЯпЖЮABЩЯШЁЕуEЃЌЪЙЁЯDCE=30ЁуЃЌСЌНгAFЃЌEFЃЎ
ЂйЧѓЁЯEAFЕФЖШЪ§ЃЛ
ЂкDEгыEFЯрЕШТ№ЃПЧыЫЕУїРэгЩЃЛ
ЃЈРрБШЬНОПЃЉ
ЃЈ2ЃЉШчЭМ2ЃЌЁїABCЮЊЕШбќжБНЧШ§НЧаЮЃЌЁЯACB=90ЁуЃЌЯШНЋШ§НЧАхЕФ90ЁуНЧгыЁЯACBжиКЯЃЌдйНЋШ§НЧАхШЦЕуCАДЫГЪБеыЗНЯђа§зЊЃЈа§зЊНЧДѓгк0ЁуЧваЁгк45ЁуЃЉЃЌа§зЊКѓШ§НЧАхЕФвЛжБНЧБпгыABНЛгкЕуDЃЌдкШ§НЧАхСэвЛжБНЧБпЩЯШЁвЛЕуFЃЌЪЙCF=CDЃЌЯпЖЮABЩЯШЁЕуEЃЌЪЙЁЯDCE=45ЁуЃЌСЌНгAFЃЌEFЃЎЧыжБНгаДГіЬНОПНсЙћЃК
ЂйЁЯEAFЕФЖШЪ§ЃЛ
ЂкЯпЖЮAEЃЌEDЃЌDBжЎМфЕФЪ§СПЙиЯЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂй120ЁуЂкDE=EFЃЛЃЈ2ЃЉЂй90ЁуЂкAE2+DB2=DE2
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉЂйгЩЕШБпШ§НЧаЮЕФаджЪЕУГіAC=BCЃЌЁЯBAC=ЁЯB=60ЁуЃЌЧѓГіЁЯACF=ЁЯBCDЃЌжЄУїЁїACFЁеЁїBCDЃЌЕУГіЁЯCAF=ЁЯB=60ЁуЃЌЧѓГіЁЯEAF=ЁЯBAC+ЁЯCAF=120ЁуЃЛ
ЂкжЄГіЁЯDCE=ЁЯFCEЃЌгЩSASжЄУїЁїDCEЁеЁїFCEЃЌЕУГіDE=EFМДПЩЃЛ
ЃЈ2ЃЉЂйгЩЕШбќжБНЧШ§НЧаЮЕФаджЪЕУГіAC=BCЃЌЁЯBAC=ЁЯB=45ЁуЃЌжЄГіЁЯACF=ЁЯBCDЃЌгЩSASжЄУїЁїACFЁеЁїBCDЃЌЕУГіЁЯCAF=ЁЯB=45ЁуЃЌAF=DBЃЌЧѓГіЁЯEAF=ЁЯBAC+ЁЯCAF=90ЁуЃЛ
ЂкжЄГіЁЯDCE=ЁЯFCEЃЌгЩSASжЄУїЁїDCEЁеЁїFCEЃЌЕУГіDE=EFЃЛдкRtЁїAEFжаЃЌгЩЙДЙЩЖЈРэЕУГіAE2+AF2=EF2ЃЌМДПЩЕУГіНсТлЃЎ
ЪдЬтНтЮіЃКНтЃКЃЈ1ЃЉЂйЁпЁїABCЪЧЕШБпШ§НЧаЮЃЌЁрAC=BCЃЌЁЯBAC=ЁЯB=60ЁуЃЎЁпЁЯDCF=60ЁуЃЌЁрЁЯACF=ЁЯBCDЃЎ
дкЁїACFКЭЁїBCDжаЃЌЁпAC=BCЃЌЁЯACF=ЁЯBCDЃЌCF=CDЃЌЁрЁїACFЁеЁїBCDЃЈSASЃЉЃЌЁрЁЯCAF=ЁЯB=60ЁуЃЌЁрЁЯEAF=ЁЯBAC+ЁЯCAF=120ЁуЃЛ
ЂкDE=EFЃЎРэгЩШчЯТЃК
ЁпЁЯDCF=60ЁуЃЌЁЯDCE=30ЁуЃЌЁрЁЯFCE=60ЁуЉ30Ёу=30ЁуЃЌЁрЁЯDCE=ЁЯFCEЃЎдкЁїDCEКЭЁїFCEжаЃЌЁпCD=CFЃЌЁЯDCE=ЁЯFCEЃЌCE=CEЃЌЁрЁїDCEЁеЁїFCEЃЈSASЃЉЃЌЁрDE=EFЃЛ
ЃЈ2ЃЉЂйЁпЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЌЁЯACB=90ЁуЃЌЁрAC=BCЃЌЁЯBAC=ЁЯB=45ЁуЃЎЁпЁЯDCF=90ЁуЃЌЁрЁЯACF=ЁЯBCDЃЎдкЁїACFКЭЁїBCDжаЃЌЁпAC=BCЃЌЁЯACF=ЁЯBCDЃЌCF=CDЃЌЁрЁїACFЁеЁїBCDЃЈSASЃЉЃЌЁрЁЯCAF=ЁЯB=45ЁуЃЌAF=DBЃЌЁрЁЯEAF=ЁЯBAC+ЁЯCAF=90ЁуЃЛ
ЂкAE2+DB2=DE2ЃЌРэгЩШчЯТЃК
ЁпЁЯDCF=90ЁуЃЌЁЯDCE=45ЁуЃЌЁрЁЯFCE=90ЁуЉ45Ёу=45ЁуЃЌЁрЁЯDCE=ЁЯFCEЃЎдкЁїDCEКЭЁїFCEжаЃЌЁпCD=CFЃЌЁЯDCE=ЁЯFCEЃЌCE=CEЃЌЁрЁїDCEЁеЁїFCEЃЈSASЃЉЃЌЁрDE=EFЃЎдкRtЁїAEFжаЃЌAE2+AF2=EF2ЃЌгжЁпAF=DBЃЌЁрAE2+DB2=DE2ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЩш
ЃЌЩш![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЕБЕу![]() дк
дк![]() ФкЃЌ
ФкЃЌ
ЂйШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
аЁУїЭЌбЇЭЈЙ§ЗжЮівбжЊЬѕМўЗЂЯжЃК![]() ЪЧЖЅНЧЮЊ
ЪЧЖЅНЧЮЊ![]() ЕФЕШбќШ§НЧаЮЃЌЧв
ЕФЕШбќШ§НЧаЮЃЌЧв![]() ЃЌДгЖјШнвзСЊЯыЕНЙЙдьвЛИіЖЅНЧЮЊ
ЃЌДгЖјШнвзСЊЯыЕНЙЙдьвЛИіЖЅНЧЮЊ![]() ЕФЕШбќШ§НЧаЮЃЎгкЪЧЃЌЫћЙ§Еу
ЕФЕШбќШ§НЧаЮЃЎгкЪЧЃЌЫћЙ§Еу![]() зї
зї![]() ЃЌЧв
ЃЌЧв![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌЗЂЯжСНИіВЛЭЌЕФШ§НЧаЮШЋЕШЃК______
ЃЌЗЂЯжСНИіВЛЭЌЕФШ§НЧаЮШЋЕШЃК______![]() _______дйРћгУШЋЕШШ§НЧаЮМАЕШбќШ§НЧаЮЕФЯрЙижЊЪЖПЩЧѓГі
_______дйРћгУШЋЕШШ§НЧаЮМАЕШбќШ§НЧаЮЕФЯрЙижЊЪЖПЩЧѓГі![]() ЕФЖШЪ§
ЕФЖШЪ§
ЧыРћгУаЁЭѕЭЌбЇЗжЮіЕФЫМТЗЃЌЭЈЙ§МЦЫуЧѓЕУ![]() ЕФЖШЪ§ЮЊ_____ЃЛ
ЕФЖШЪ§ЮЊ_____ЃЛ
ЂкаЁЭѕдкЂйЕФЛљДЁЩЯНјвЛВННјааЬНЫїЃЌЗЂЯж![]() жЎМфДцдквЛжжЬиЪтЕФЕШСПЙиЯЕЃЌЧыаДГіетИіЕШСПЙиЯЕЃЌВЂМгвджЄУїЃЎ
жЎМфДцдквЛжжЬиЪтЕФЕШСПЙиЯЕЃЌЧыаДГіетИіЕШСПЙиЯЕЃЌВЂМгвджЄУїЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌЕу![]() дк
дк![]() ЭтЃЌФЧУД
ЭтЃЌФЧУД![]() жЎМфЕФЪ§СПЙиЯЕЪЧЗёИФБфЃПШєИФБфЃЌЧыжБНгаДГіЫќУЧЕФЪ§СПЙиЯЕЃЛШєВЛБфЃЌЧыЫЕУїРэгЩЃЎ
жЎМфЕФЪ§СПЙиЯЕЪЧЗёИФБфЃПШєИФБфЃЌЧыжБНгаДГіЫќУЧЕФЪ§СПЙиЯЕЃЛШєВЛБфЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЕШбќ![]() жаЃЌ
жаЃЌ![]() ЃЌАб
ЃЌАб![]() би
би![]() елЕўЃЌЕу
елЕўЃЌЕу![]() ЕФЖдгІЕуЮЊ
ЕФЖдгІЕуЮЊ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌЪЙ
ЃЌЪЙ![]() ЦНЗж
ЦНЗж![]() ЃЌШє
ЃЌШє![]() ЃЌдђЕу
ЃЌдђЕу![]() ЪЧЃЈ ЃЉ
ЪЧЃЈ ЃЉ
A.![]() ЕФФкаФB.
ЕФФкаФB.![]() ЕФЭтаФC.
ЕФЭтаФC.![]() ЕФФкаФD.
ЕФФкаФD.![]() ЕФЭтаФ
ЕФЭтаФ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌAB=4ЃЌAD=3ЃЌОиаЮФкВПгавЛЖЏЕуPТњзуSЁїPAB=![]() SОиаЮABCDЃЌдђЕуPЕНAЁЂBСНЕуЕФОрРыжЎКЭPA+PBЕФзюаЁжЕЮЊ______ЃЎ
SОиаЮABCDЃЌдђЕуPЕНAЁЂBСНЕуЕФОрРыжЎКЭPA+PBЕФзюаЁжЕЮЊ______ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
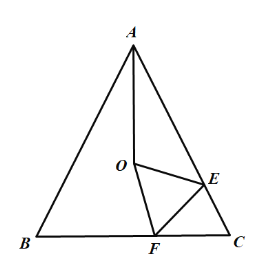
ЁОЬтФПЁПЃЈ1ЃЉШчЭМ1ЃЌНЋОиаЮABCDелЕўЃЌЪЙBCТфдкЖдНЧЯпBDЩЯЃЌелКлЮЊBEЃЌЕуCТфдкЕуC'ДІЃЌШєЁЯADB=54ЁуЃЌдђЁЯDBEЕФЖШЪ§ЮЊ ЁуЃЎ
ЃЈ2ЃЉаЁУїЪжжагавЛеХОиаЮжНЦЌABCDЃЌAB=4ЃЌAD=9ЃЎЃЈЛвЛЛЃЉШчЭМ2ЃЌЕуEдкетеХОиаЮжНЦЌЕФБпADЩЯЃЌНЋжНЦЌелЕўЃЌЪЙABТфдкCEЫљдкжБЯпЩЯЃЌелКлЩшЮЊMNЃЈЕуMЃЌNЗжБ№дкБпADЃЌBCЩЯЃЉЃЌРћгУжБГпКЭдВЙцЛГіелКлMNЃЈВЛаДзїЗЈЃЌБЃСєзїЭМКлМЃЃЌВЂгУКкЩЋЫЎБЪАбЯпЖЮMNУшЧхГўЃЉЃЛ
ЃЈ3ЃЉЃЈЫувЛЫуЃЉШчЭМ3ЃЌЕуFдкетеХОиаЮжНЦЌЕФБпBCЩЯЃЌНЋжНЦЌелЕўЃЌЪЙFBТфдкЩфЯпFDЩЯЃЌелКлЮЊGFЃЌЕуAЃЌBЗжБ№ТфдкЕуA'ЃЌB'ДІЃЌШєAG=![]() ЃЌЧѓB'DЕФГЄЃЛ
ЃЌЧѓB'DЕФГЄЃЛ
ЃЈ4ЃЉЃЈбщвЛбщЃЉШчЭМ4ЃЌЕуKдкетеХОиаЮжНЦЌЕФБпADЩЯЃЌDK=3ЃЌНЋжНЦЌелЕўЃЌЪЙABТфдкCKЫљдкжБЯпЩЯЃЌелКлЮЊHIЃЌЕуAЃЌBЗжБ№ТфдкЕуA'ЃЌB'ДІЃЌаЁУїШЯЮЊB'IЫљдкжБЯпЧЁКУОЙ§ЕуDЃЌЫћЕФХаЖЯЪЧЗёе§ШЗЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌФГГЌЪаДгвЛТЅЕНЖўТЅгавЛздЖЏЗіЬнЃЌЭМ2ЪЧВрУцЪОвтЭМЃЎвбжЊздЖЏЗіЬнABЕФЦТЖШЮЊ1ЃК2ЃЎ4ЃЌABЕФГЄЖШЪЧ13УзЃЌMNЪЧЖўТЅТЅЖЅЃЌMNЁЮPQЃЌCЪЧMNЩЯДІдкздЖЏЗіЬнЖЅЖЫBЕуе§ЩЯЗНЕФвЛЕуЃЌBCЁЭMNЃЌдкздЖЏЗіЬнЕзЖЫAДІВтЕУCЕуЕФбіНЧЮЊ42ЁуЃЌЧѓЖўТЅЕФВуИпBCдМЮЊЖрЩйУзЃПЃЈ sin42ЁуЁж0ЃЎ7ЃЌtan42ЁуЁж0ЃЎ9ЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
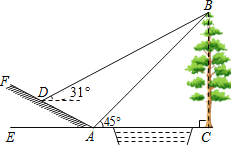
ЁОЬтФПЁПЪ§бЇЛюЖЏПЮЩЯЃЌаЁУїКЭаЁКьвЊВтСПаЁКгЖдАЖДѓЪїBCЕФИпЖШЃЌаЁКьдкЕуAВтЕУДѓЪїЖЅЖЫBЕФбіНЧЮЊ45ЁуЃЌаЁУїДгAЕуГіЗЂбиаБЦТзп3![]() УзЕНДяаБЦТЩЯЕуDЃЌдкДЫДІВтЕУЪїЖЅЖЫЕуBЕФбіНЧЮЊ31ЁуЃЌЧваБЦТAFЕФЦТБШЮЊ1ЃК2ЃЎ
УзЕНДяаБЦТЩЯЕуDЃЌдкДЫДІВтЕУЪїЖЅЖЫЕуBЕФбіНЧЮЊ31ЁуЃЌЧваБЦТAFЕФЦТБШЮЊ1ЃК2ЃЎ
ЃЈ1ЃЉЧѓаЁУїДгЕуAЕНЕуDЕФЙ§ГЬжаЃЌЫћЩЯЩ§ЕФИпЖШЃЛ
ЃЈ2ЃЉвРОнЫћУЧВтСПЕФЪ§ОнФмЗёЧѓГіДѓЪїBCЕФИпЖШЃПШєФмЃЌЧыМЦЫуЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎЃЈВЮПМЪ§ОнЃКsin31ЁуЁж0.52ЃЌcos31ЁуЁж0.86ЃЌtan31ЁуЁж0.60ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
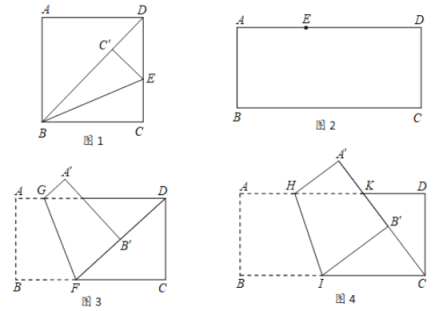
ЁОЬтФПЁПдкЁїABC жаЃЌAB=ACЃЌЕу M дк BA ЕФбгГЄЯпЩЯЃЌЕу N дк BC ЕФбгГЄЯпЩЯЃЌЙ§Еу C зїCDЁЮAB НЛЁЯCAM ЕФЦНЗжЯпгкЕу DЃЎ
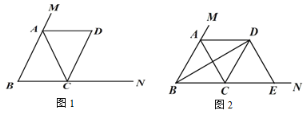
ЃЈ1ЃЉШчЭМ 1ЃЌЧѓжЄЃКЫФБпаЮ ABCD ЪЧЦНааЫФБпаЮЃЛ
ЃЈ2ЃЉШчЭМ 2ЃЌЕБЁЯABC=60ЁуЪБЃЌСЌНг BDЃЌЙ§Еу D зї DEЁЭBDЃЌНЛ BN гкЕу EЃЌдкВЛЬэМгШЮКЮИЈжњЯпЕФЧщПіЯТЃЌЧыжБНгаДГіЭМ 2 жаЫФИіШ§НЧаЮЃЈВЛАќКЌЁїCDEЃЉЃЌЪЙаДГіЕФУПИіШ§НЧаЮЕФУцЛ§гыЁїCDE ЕФУцЛ§ЯрЕШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГбЇаЃАЫЁЂОХСНИіФъМЖИїгабЇЩњ180ШЫЃЌЮЊСЫНтетСНИіФъМЖбЇЩњЕФЬхжЪНЁПЕЧщПіЃЌНјааСЫГщбљЕїВщЃЌОпЬхЙ§ГЬШчЯТЃК
ЁЁЁЁЪеМЏЪ§Он
ДгАЫЁЂОХСНИіФъМЖИїЫцЛњГщШЁ20УћбЇЩњНјааЬхжЪНЁПЕВтЪдЃЌВтЪдГЩМЈЃЈАйЗжжЦЃЉШчЯТЃК
АЫФъМЖ | 78 | 86 | 74 | 81 | 75 | 76 | 87 | 70 | 75 | 90 |
75 | 79 | 81 | 70 | 74 | 80 | 86 | 69 | 83 | 77 | |
ОХФъМЖ | 93 | 73 | 88 | 81 | 72 | 81 | 94 | 83 | 77 | 83 |
80 | 81 | 70 | 81 | 73 | 78 | 82 | 80 | 70 | 40 |
ећРэЁЂУшЪіЪ§Он
НЋГЩМЈАДШчЯТЗжЖЮећРэЁЂУшЪіетСНзщбљБОЪ§ОнЃК
ГЩМЈЃЈxЃЉ | 40ЁмxЁм49 | 50ЁмxЁм59 | 60ЁмxЁм69 | 70ЁмxЁм79 | 80ЁмxЁм89 | 90ЁмxЁм100 |
АЫФъМЖШЫЪ§ | 0 | 0 | 1 | 11 | 7 | 1 |
ОХФъМЖШЫЪ§ | 1 | 0 | 0 | 7 | 10 | 2 |
ЃЈЫЕУїЃКГЩМЈ80ЗжМАвдЩЯЮЊЬхжЪНЁПЕгХауЃЌ70ЁЋ79ЗжЮЊЬхжЪНЁПЕСМКУЃЌ60ЁЋ69ЗжЮЊЬхжЪНЁПЕКЯИёЃЌ60ЗжвдЯТЮЊЬхжЪНЁПЕВЛКЯИёЃЉ
ЁЁЁЁЗжЮіЪ§Он
СНзщбљБОЪ§ОнЕФЦНОљЪ§ЁЂжаЮЛЪ§ЁЂжкЪ§ЁЂЗНВюШчБэЫљЪОЃК
ФъМЖ | ЦНОљЪ§ | жаЮЛЪ§ | жкЪ§ | ЗНВю |
АЫФъМЖ | 78.3 | 77.5 | 75 | 33.6 |
ОХФъМЖ | 78 | 80.5 | a | 52.1 |
ЃЈ1ЃЉБэИёжаaЕФжЕЮЊ______ЃЛ
ЃЈ2ЃЉЧыФуЙРМЦИУаЃОХФъМЖЬхжЪНЁПЕгХауЕФбЇЩњШЫЪ§ЮЊЖрЩйЃП
ЃЈ3ЃЉИљОнвдЩЯаХЯЂЃЌФуШЯЮЊФФИіФъМЖбЇЩњЕФЬхжЪНЁПЕЧщПіИќКУвЛаЉЃПЧыЫЕУїРэгЩЃЎЃЈЧыДгСНИіВЛЭЌЕФНЧЖШЫЕУїЭЦЖЯЕФКЯРэадЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com