
ЁОЬтФПЁПдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЩш
ЃЌЩш![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
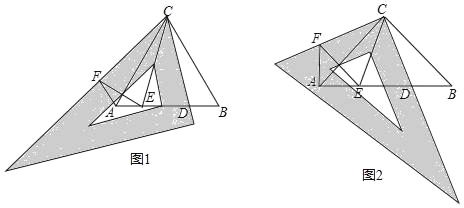
ЃЈ1ЃЉШчЭМ1ЃЌЕБЕу![]() дк
дк![]() ФкЃЌ
ФкЃЌ
ЂйШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
аЁУїЭЌбЇЭЈЙ§ЗжЮівбжЊЬѕМўЗЂЯжЃК![]() ЪЧЖЅНЧЮЊ
ЪЧЖЅНЧЮЊ![]() ЕФЕШбќШ§НЧаЮЃЌЧв
ЕФЕШбќШ§НЧаЮЃЌЧв![]() ЃЌДгЖјШнвзСЊЯыЕНЙЙдьвЛИіЖЅНЧЮЊ
ЃЌДгЖјШнвзСЊЯыЕНЙЙдьвЛИіЖЅНЧЮЊ![]() ЕФЕШбќШ§НЧаЮЃЎгкЪЧЃЌЫћЙ§Еу
ЕФЕШбќШ§НЧаЮЃЎгкЪЧЃЌЫћЙ§Еу![]() зї
зї![]() ЃЌЧв
ЃЌЧв![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌЗЂЯжСНИіВЛЭЌЕФШ§НЧаЮШЋЕШЃК______
ЃЌЗЂЯжСНИіВЛЭЌЕФШ§НЧаЮШЋЕШЃК______![]() _______дйРћгУШЋЕШШ§НЧаЮМАЕШбќШ§НЧаЮЕФЯрЙижЊЪЖПЩЧѓГі
_______дйРћгУШЋЕШШ§НЧаЮМАЕШбќШ§НЧаЮЕФЯрЙижЊЪЖПЩЧѓГі![]() ЕФЖШЪ§
ЕФЖШЪ§
ЧыРћгУаЁЭѕЭЌбЇЗжЮіЕФЫМТЗЃЌЭЈЙ§МЦЫуЧѓЕУ![]() ЕФЖШЪ§ЮЊ_____ЃЛ
ЕФЖШЪ§ЮЊ_____ЃЛ
ЂкаЁЭѕдкЂйЕФЛљДЁЩЯНјвЛВННјааЬНЫїЃЌЗЂЯж![]() жЎМфДцдквЛжжЬиЪтЕФЕШСПЙиЯЕЃЌЧыаДГіетИіЕШСПЙиЯЕЃЌВЂМгвджЄУїЃЎ
жЎМфДцдквЛжжЬиЪтЕФЕШСПЙиЯЕЃЌЧыаДГіетИіЕШСПЙиЯЕЃЌВЂМгвджЄУїЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌЕу![]() дк
дк![]() ЭтЃЌФЧУД
ЭтЃЌФЧУД![]() жЎМфЕФЪ§СПЙиЯЕЪЧЗёИФБфЃПШєИФБфЃЌЧыжБНгаДГіЫќУЧЕФЪ§СПЙиЯЕЃЛШєВЛБфЃЌЧыЫЕУїРэгЩЃЎ
жЎМфЕФЪ§СПЙиЯЕЪЧЗёИФБфЃПШєИФБфЃЌЧыжБНгаДГіЫќУЧЕФЪ§СПЙиЯЕЃЛШєВЛБфЃЌЧыЫЕУїРэгЩЃЎ

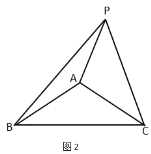
ЁОД№АИЁПЃЈ1ЃЉЂйЁїBADЃЌЁїCAPЃЌ 63ЁуЃЛЂкІТЉІСЃН90ЁуЃЛЃЈ2ЃЉИФБфЃЌІС+ІТЃН90ЁуЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЂйЯШжЄУїЁїBADЁеЁїCAPЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУЕНCPЃНBDЃЌИљОнЕШбќШ§НЧаЮЕФаджЪНтД№ЃЛЂкЗТееЂйЕФзїЗЈНтД№МДПЩЃЛ
ЃЈ2ЃЉЙ§ЕуAзї![]() ЃЌЧвADЃНAPЃЌСЌНгDPЃЌDBЃЌжЄУїЁїBADЁеЁїCAPЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУЕНPCЃНBDЃЌНсКЯЭМаЮМЦЫуМДПЩЃЎ
ЃЌЧвADЃНAPЃЌСЌНгDPЃЌDBЃЌжЄУїЁїBADЁеЁїCAPЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУЕНPCЃНBDЃЌНсКЯЭМаЮМЦЫуМДПЩЃЎ
НтЃКЃЈ1ЃЉЂйЁп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁрЁЯBACЃНЁЯDAPЃЌ
ЁрЁЯBADЃНЁЯCAPЃЌ
дкЁїBADКЭЁїCAPжаЃЌ
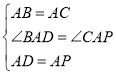 ЃЌ
ЃЌ
ЁрЁїBADЁеЁїCAPЃЈSASЃЉЃЌ
ЁрBDЃНCPЃЌЁЯBDAЃНЁЯAPCЃЌ
Ёп![]() ЃЌ
ЃЌ
ЁрBDЃН![]() ЃЌ
ЃЌ
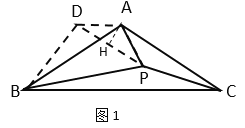
ШчЭМЃЌЙ§ЕуAзїAHЁЭDPЃЌДЙзуЮЊЕуHЃЌ
Ёп![]() ЃЌЧв
ЃЌЧв![]() ЃЌ
ЃЌ
ЁрЁЯAPDЃНЁЯADPЃН30ЁуЃЌ
дкRtЁїAPHжаЃЌcosЁЯAPH=![]() ,
,
Ёрcos30Ёу=![]() ,
,
Ёр![]()
Ёп![]() ЃЌAHЁЭDPЃЌ
ЃЌAHЁЭDPЃЌ
ЁрDPЃН2PHЃН![]() ЃЌ
ЃЌ
ЁрBDЃНDPЃЌ
ЁрЁЯBPDЃНЁЯPBDЃЌ
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]()
Ёп![]() ЃЌЁЯAPDЃН30ЁуЃЌ
ЃЌЁЯAPDЃН30ЁуЃЌ
ЁрЁЯBPDЃНЁЯPBDЃН![]()
ЁрЁЯBDPЃН![]() ЃЌ
ЃЌ
ЁрЁЯBDAЃНЁЯBDP+ЁЯADPЃН![]() ЃЌ
ЃЌ
ЁпЁЯBDAЃНЁЯAPCЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃКЁїBADЃЌЁїCAPЃЌ 63ЁуЃЛ
ЂкІТЉІСЃН90ЁуЃЌ
РэгЩШчЯТЃКгЩЂйЕУ
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌЁЯAPDЃН30ЁуЃЌ
ЃЌЁЯAPDЃН30ЁуЃЌ
ЁрЁЯBPDЃНЁЯPBDЃН![]() ЃЌ
ЃЌ
ЁрЁЯBDPЃН![]() ЃЌ
ЃЌ
ЁрЁЯBDAЃНЁЯBDP+ЁЯADPЃН![]() ЃЌ
ЃЌ
ЁпЁЯBDAЃНЁЯAPCЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрІТЉІСЃН90ЁуЃЌ
ЃЈ2ЃЉИФБфЃЌІС+ІТЃН90ЁуЃЌРэгЩШчЯТЃК
Й§ЕуAзїЁЯDAPЃН120ЁуЃЌЧвADЃНAPЃЌСЌНгDPЃЌDBЃЌЙ§ЕуAзїAHЁЭDPЃЌДЙзуЮЊЕуHЃЌ
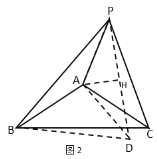
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁрЁЯBACЃНЁЯDAPЃЌ
ЁрЁЯBADЃНЁЯCAPЃЌ
дкЁїBADКЭЁїCAPжаЃЌ
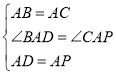 ЃЌ
ЃЌ
ЁрЁїBADЁеЁїCAPЃЈSASЃЉЃЌ
ЁрBDЃНCPЃЌЁЯBDAЃНЁЯAPCЃЌ
Ёп![]() ЃЌ
ЃЌ
ЁрBDЃН![]() ЃЌ
ЃЌ
Ёп![]() ЃЌЧв
ЃЌЧв![]() ЃЌ
ЃЌ
ЁрЁЯAPDЃНЁЯADPЃН30ЁуЃЌ
дкRtЁїAPHжаЃЌcosЁЯAPH=![]() ,
,
Ёрcos30Ёу=![]() ,
,
Ёр![]()
Ёп![]() ЃЌAHЁЭDPЃЌ
ЃЌAHЁЭDPЃЌ
ЁрDPЃН2PHЃН![]() ЃЌ
ЃЌ
ЁрBDЃНDPЃЌ
ЁрЁЯBPDЃНЁЯPBDЃЌ
Ёп![]() ЃЌЁЯAPDЃН30ЁуЃЌ
ЃЌЁЯAPDЃН30ЁуЃЌ
ЁрЁЯBPDЃНЁЯPBDЃНЁЯAPB+ЁЯAPDЃН![]() +30ЁуЃЌ
+30ЁуЃЌ
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁрЁЯADBЃН![]() ЃЌ
ЃЌ
гжЁпЁЯADPЃН30ЁуЃЌ
ЁрЁЯBDPЃНЁЯADB+ЁЯADPЃН![]() +30Ёу,
+30Ёу,
ЁпЁЯBPD+ЁЯPBD+ЁЯBDPЃН180Ёу,
Ёр![]() +30Ёу+
+30Ёу+![]() +30Ёу+
+30Ёу+![]() +30ЁуЃН180Ёу,
+30ЁуЃН180Ёу,
ЁрІС+ІТЃН90ЁуЃЌ
ЁрІСЁЂІТжЎМфЕФЪ§СПЙиЯЕИФБфЮЊІС+ІТЃН90ЁуЃЎ


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
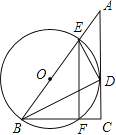
ЁОЬтФПЁПдкRtЁїABCжаЃЌBC=9ЃЌ CA=12ЃЌЁЯABCЕФЦНЗжЯпBDНЛACгыЕуDЃЌ DEЁЭDBНЛABгкЕуEЃЎ
ЃЈ1ЃЉЩшЁбOЪЧЁїBDEЕФЭтНгдВЃЌЧѓжЄЃКACЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉЩшЁбOНЛBCгкЕуFЃЌСЌНсEFЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЖўДЮКЏЪ§![]() ЕФЭМЯѓгы
ЕФЭМЯѓгы![]() жсНЛгк
жсНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌгы
СНЕуЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌ
ЃЌ![]() ЕФАыОЖЮЊ
ЕФАыОЖЮЊ![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() ЩЯвЛЖЏЕуЃЎ
ЩЯвЛЖЏЕуЃЎ
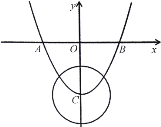
ЃЈ1ЃЉЧѓЕу![]() ЃЌ
ЃЌ![]() ЕФзјБъЃП
ЕФзјБъЃП
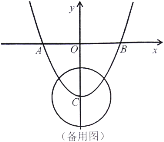
ЃЈ2ЃЉЪЧЗёДцдкЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЮЊжБНЧШ§НЧаЮЃПШєДцдкЃЌЧѓГіЕу
ЮЊжБНЧШ§НЧаЮЃПШєДцдкЃЌЧѓГіЕу![]() ЕФзјБъЃКШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃКШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдке§ЗНаЮ![]() жаЃЌ
жаЃЌ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЩЯЕФЕуЃЌЧв
ЩЯЕФЕуЃЌЧв![]() ЃЌдђгаНсТл
ЃЌдђгаНсТл![]() ГЩСЂЃЛ
ГЩСЂЃЛ
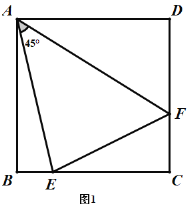
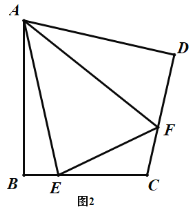
![]() ШчЭМ2ЃЌдкЫФБпаЮ
ШчЭМ2ЃЌдкЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЩЯЕФЕуЃЌЧв
ЩЯЕФЕуЃЌЧв![]() ЪЧ
ЪЧ![]() ЕФвЛАыЃЌ ФЧУДНсТл
ЕФвЛАыЃЌ ФЧУДНсТл![]() ЪЧЗёШдШЛГЩСЂ?ШєГЩСЂЃЌЧыжЄУїЃЛВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЎ
ЪЧЗёШдШЛГЩСЂ?ШєГЩСЂЃЌЧыжЄУїЃЛВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЎ
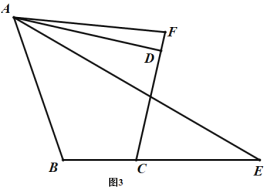
![]() ШєНЋ
ШєНЋ![]() жаЕФЬѕМўИФЮЊЃКШчЭМ3ЃЌдкЫФБпаЮ
жаЕФЬѕМўИФЮЊЃКШчЭМ3ЃЌдкЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌбгГЄ
ЃЌбгГЄ![]() ЕНЕу
ЕНЕу![]() ЃЌбгГЄ
ЃЌбгГЄ![]() ЕНЕу
ЕНЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ШдШЛЪЧ
ШдШЛЪЧ![]() ЕФвЛАыЃЌдђНсТл
ЕФвЛАыЃЌдђНсТл![]() ЪЧЗёШдШЛГЩСЂ?ШєГЩСЂЃЌЧыжЄУїЃЛВЛГЩСЂЃЌЧыаДГіЫќУЧЕФЪ§СПЙиЯЕВЂжЄУї
ЪЧЗёШдШЛГЩСЂ?ШєГЩСЂЃЌЧыжЄУїЃЛВЛГЩСЂЃЌЧыаДГіЫќУЧЕФЪ§СПЙиЯЕВЂжЄУї
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬГЁЯњЪлвЛжжНјМлЮЊУПМў10дЊЕФШегУЩЬЦЗЃЌОЕїВщЗЂЯжЃЌИУЩЬЦЗУПЬьЕФЯњЪлСП![]() ЃЈМўЃЉгыЯњЪлЕЅМл
ЃЈМўЃЉгыЯњЪлЕЅМл![]() ЃЈдЊЃЉТњзу
ЃЈдЊЃЉТњзу![]() ЃЌЩшЯњЪлетжжЩЬЦЗУПЬьЕФРћШѓЮЊ
ЃЌЩшЯњЪлетжжЩЬЦЗУПЬьЕФРћШѓЮЊ![]() ЃЈдЊЃЉ.
ЃЈдЊЃЉ.
ЃЈ1ЃЉЧѓ![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉдкБЃжЄЯњЪлСПОЁПЩФмДѓЕФЧАЬсЯТЃЌИУЩЬГЁУПЬьЛЙЯыЛёЕУ2000дЊЕФРћШѓЃЌгІНЋЯњЪлЕЅМлЖЈЮЊЖрЩйдЊЃП
ЃЈ3ЃЉЕБУПЬьЯњЪлСПВЛЩйгк50МўЃЌЧвЯњЪлЕЅМлжСЩйЮЊ32дЊЪБЃЌИУЩЬГЁУПЬьЛёЕУЕФзюДѓРћШѓЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЪЧвЛжжМђвзЕФЪжЛњМмЃЌНЋЦфНсЙЙМђЛЏЮЊЭМ2ЃЌгЩППАх![]() ЃЌЕззљ
ЃЌЕззљ![]() КЭЖЅАх
КЭЖЅАх![]() зщГЩЃЌВтЕУ
зщГЩЃЌВтЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЪжЛњМмЕФИпЃЈЕу![]() ЕН
ЕН![]() ЕФОрРыЃЉЃЛ
ЕФОрРыЃЉЃЛ
ЃЈ2ЃЉЧыЭЈЙ§МЦЫуШЗЖЈКёЖШЮЊ![]() ЕФЪжЛњЗХжУдкЪжЛњМмЩЯФмЗёгаЕїНкНЧЖШЕФПеМфЃЎ
ЕФЪжЛњЗХжУдкЪжЛњМмЩЯФмЗёгаЕїНкНЧЖШЕФПеМфЃЎ
ЃЈВЮПМЪ§ОнЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌНсЙћОЋШЗЕН0.1
ЃЌНсЙћОЋШЗЕН0.1![]() ЃЉ
ЃЉ


ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПГЄФ§ДѓЫтВњгкгмДЮЧјГЄФ§еђЃЌжжжВРњЪЗгЦОУЃЌЧхГѕдјБЛбЁЮЊЛЪМвЙБЦЗЃЌдкНњжавдМАЪЁФкЭтЯэгаЪЂгўЃЎЧяЬьЧкРЭЕФХЉУёУЧНЋДѓЫтБрГЩДЎКѓНјааЯњЪлЃЎаЁРжЭЈЙ§ЭјЕъЭЦЙуМвЯчЬиВњЃЌЯњЪлДѓЫтЃЎУПДЎДѓЫтЕФГЩБОЪЧ6дЊЃЌЯњЪлвЛЖЮЪБМфКѓЃЌЗЂЯжЕБЪлМлЮЊУПДЎ25дЊЪБЃЌЦНОљУПЬьФмЪлГі12ДЎЃЎаЁРжЯыШУИќЖрЕФШЫГЂЕНГЄФ§ДѓЫтЃЌвђДЫНјааСЫНЕМлЯњЪлЃЌОЕїВщЗЂЯжЃЌУПДЎДѓЫтУПНЕМл0.5дЊЃЌЦНОљУПЬьЖрЪлГі2ДЎЃЎШєаЁРжМШЯыБЃжЄЦНОљУПЬьЛёРћ420дЊЃЌгжЯыРЉДѓЯњЪлСПЃЌФЧУДУПДЎДѓЫтгІНЕМлЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
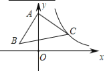
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌЖЅЕу
ЃЌЖЅЕу![]() дк
дк![]() жсЩЯЃЌЖЅЕу
жсЩЯЃЌЖЅЕу![]() дкЗДБШР§КЏЪ§
дкЗДБШР§КЏЪ§![]() ЕФЭМЯѓЩЯЃЌвбжЊЕу
ЕФЭМЯѓЩЯЃЌвбжЊЕу![]() ЕФзнзјБъЪЧ 3ЃЌдђОЙ§Еу
ЕФзнзјБъЪЧ 3ЃЌдђОЙ§Еу![]() ЕФЗДБШР§КЏЪ§ЕФНтЮіЪНЮЊ_____________
ЕФЗДБШР§КЏЪ§ЕФНтЮіЪНЮЊ_____________
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈВйзїЗЂЯжЃЉ
ЃЈ1ЃЉШчЭМ1ЃЌЁїABCЮЊЕШБпШ§НЧаЮЃЌЯШНЋШ§НЧАхжаЕФ60ЁуНЧгыЁЯACBжиКЯЃЌдйНЋШ§НЧАхШЦЕуCАДЫГЪБеыЗНЯђа§зЊЃЈа§зЊНЧДѓгк0ЁуЧваЁгк30ЁуЃЉЃЌа§зЊКѓШ§НЧАхЕФвЛжБНЧБпгыABНЛгкЕуDЃЌдкШ§НЧАхаББпЩЯШЁвЛЕуFЃЌЪЙCF=CDЃЌЯпЖЮABЩЯШЁЕуEЃЌЪЙЁЯDCE=30ЁуЃЌСЌНгAFЃЌEFЃЎ
ЂйЧѓЁЯEAFЕФЖШЪ§ЃЛ
ЂкDEгыEFЯрЕШТ№ЃПЧыЫЕУїРэгЩЃЛ
ЃЈРрБШЬНОПЃЉ
ЃЈ2ЃЉШчЭМ2ЃЌЁїABCЮЊЕШбќжБНЧШ§НЧаЮЃЌЁЯACB=90ЁуЃЌЯШНЋШ§НЧАхЕФ90ЁуНЧгыЁЯACBжиКЯЃЌдйНЋШ§НЧАхШЦЕуCАДЫГЪБеыЗНЯђа§зЊЃЈа§зЊНЧДѓгк0ЁуЧваЁгк45ЁуЃЉЃЌа§зЊКѓШ§НЧАхЕФвЛжБНЧБпгыABНЛгкЕуDЃЌдкШ§НЧАхСэвЛжБНЧБпЩЯШЁвЛЕуFЃЌЪЙCF=CDЃЌЯпЖЮABЩЯШЁЕуEЃЌЪЙЁЯDCE=45ЁуЃЌСЌНгAFЃЌEFЃЎЧыжБНгаДГіЬНОПНсЙћЃК
ЂйЁЯEAFЕФЖШЪ§ЃЛ
ЂкЯпЖЮAEЃЌEDЃЌDBжЎМфЕФЪ§СПЙиЯЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com