
【题目】在Rt△ABC中,BC=9, CA=12,∠ABC的平分线BD交AC与点D, DE⊥DB交AB于点E.
(1)设⊙O是△BDE的外接圆,求证:AC是⊙O的切线;
(2)设⊙O交BC于点F,连结EF,求![]() 的值.
的值.
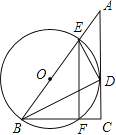
【答案】(1)见详解;
(2)![]() .
.
【解析】
(1)因为点D在⊙O上,所以只要连结圆心和圆上这点,证明OD和AC垂直即可.
利用角平分线、等腰三角形、直角三角形两锐角互余,完成证明.
(2)利用勾股定理求得AB的长.;利用△ADO∽△ACB对应线段成比例求得BE的长;利用△BEF∽△BAC得![]() =
=![]() ,从而问题得解.
,从而问题得解.
(1)证明:由已知DE⊥DB,⊙O是Rt△BDE的外接圆,
∴BE是⊙O的直径,点O是BE的中点,连结OD,
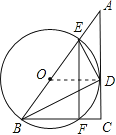
∵![]() ,∴
,∴![]() .
.
又∵BD为∠ABC的平分线,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() ,即∴
,即∴![]()
又∵OD是⊙O的半径,
∴AC是⊙O的切线.
(2) 解:设⊙O的半径为r, 在Rt△ABC中,![]() ,
,
∴![]()
∵![]() ,
,![]() ,∴△ADO∽△ACB.
,∴△ADO∽△ACB.
∴![]() .∴
.∴![]() .
.
∴![]() .∴
.∴![]()
又∵BE是⊙O的直径.∴![]() .∴△BEF∽△BAC
.∴△BEF∽△BAC
∴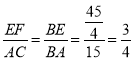 .
.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴相交于点C(0,3),且
轴相交于点C(0,3),且![]() ,
,![]() ,抛物线的顶点为
,抛物线的顶点为![]() .
.
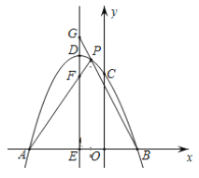
(1)求![]() 、
、![]() 两点的坐标.
两点的坐标.
(2)求抛物线的表达式.
(3)过点![]() 作直线
作直线![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,点
,点![]() 是抛物线上
是抛物线上![]() ,
,![]() 两点间的一个动点(点
两点间的一个动点(点![]() 不与
不与![]() 、
、![]() 两点重合),
两点重合),![]() 、
、![]() 与直线
与直线![]() 分别相交于点
分别相交于点![]() 、
、![]() 当点
当点![]() 运动时,
运动时,![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
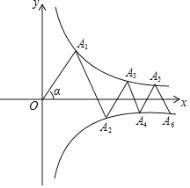
【题目】如图,点A1、A3、A5…在反比例函数y=![]() (x>0)的图象上,点A2、A4、A6……在反比例函数y=-
(x>0)的图象上,点A2、A4、A6……在反比例函数y=-![]() (x>0)的图象上,∠OA1A2=∠A1A2A3=∠A2A3A4=…=∠α=60°,且OA1=2,则An(n为正整数)的纵坐标为________________________________.(用含n的式子表示)
(x>0)的图象上,∠OA1A2=∠A1A2A3=∠A2A3A4=…=∠α=60°,且OA1=2,则An(n为正整数)的纵坐标为________________________________.(用含n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
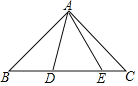
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,点D,E均在边BC上,且∠DAE=45°
(1)若BD=2,CE=4,则DE=_____.
(2)若∠AEB=75°,则线段BD与CE的数量关系是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
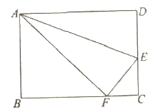
【题目】如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,使点D恰好落在BC边上的F点处.已知折痕AE=10![]() ,且CE:CF=4:3,那么该矩形的周长为( )
,且CE:CF=4:3,那么该矩形的周长为( )
A.48B.64C.92D.96
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系 xOy 中,直线 l:![]() 与 x 轴交于点 A(-2,0),与 y 轴交于点 B.双曲线
与 x 轴交于点 A(-2,0),与 y 轴交于点 B.双曲线![]() 与直线 l 交于 P,Q 两点,其中点 P 的纵坐标大于点 Q 的纵坐标.
与直线 l 交于 P,Q 两点,其中点 P 的纵坐标大于点 Q 的纵坐标.
(1)求点 B 的坐标;
(2)当点 P 的横坐标为 2 时,求 k 的值;
(3)连接 PO,记△POB 的面积为 S,若![]() ,直接写出 k 的取值范围.
,直接写出 k 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,设
,设![]() ,
,![]() .
.
(1)如图1,当点![]() 在
在![]() 内,
内,
①若![]() ,求
,求![]() 的度数;
的度数;
小明同学通过分析已知条件发现:![]() 是顶角为
是顶角为![]() 的等腰三角形,且
的等腰三角形,且![]() ,从而容易联想到构造一个顶角为
,从而容易联想到构造一个顶角为![]() 的等腰三角形.于是,他过点
的等腰三角形.于是,他过点![]() 作
作![]() ,且
,且![]() ,连接
,连接![]() ,发现两个不同的三角形全等:______
,发现两个不同的三角形全等:______![]() _______再利用全等三角形及等腰三角形的相关知识可求出
_______再利用全等三角形及等腰三角形的相关知识可求出![]() 的度数
的度数
请利用小王同学分析的思路,通过计算求得![]() 的度数为_____;
的度数为_____;
②小王在①的基础上进一步进行探索,发现![]() 之间存在一种特殊的等量关系,请写出这个等量关系,并加以证明.
之间存在一种特殊的等量关系,请写出这个等量关系,并加以证明.
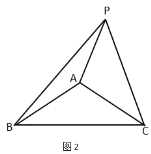
(2)如图2,点![]() 在
在![]() 外,那么
外,那么![]() 之间的数量关系是否改变?若改变,请直接写出它们的数量关系;若不变,请说明理由.
之间的数量关系是否改变?若改变,请直接写出它们的数量关系;若不变,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com