
【题目】如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,使点D恰好落在BC边上的F点处.已知折痕AE=10![]() ,且CE:CF=4:3,那么该矩形的周长为( )
,且CE:CF=4:3,那么该矩形的周长为( )
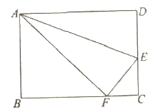
A.48B.64C.92D.96
【答案】D
【解析】
由CE:CF=4:3,可以假设CE=4k,CF=3k推出EF=DE=5k,AB=CD=9k,利用相似三角形的性质求出BF,再在Rt△ADE中,利用勾股定理构建方程即可解决问题.
∵四边形ABCD是矩形,
∴AB=CD,AD=BC,∠B=∠C=∠D=90°,
∵CE:CF=4:3,
∴可以假设CE=4k,CF=3k
∴EF=DE=5k,AB=CD=9k,
∵∠AFE=∠D=90°,
∴∠AFB+∠EFC=90°,∠EFC+∠FEC=90°,
∴∠AFB=∠CEF,
∴△ABF∽△FCE,
∴![]() ,
,
∴![]() ,
,
∴BF=12k,
∴AD=BC=15k,
在Rt△AED中,∵AE2=AD2+DE2,
∴1000=225k2+25k2,
∴k=2或-2(舍弃),
∴矩形的周长=48k=96,
故选D.


科目:初中数学 来源: 题型:
【题目】在直角坐标系中,![]() 的三个顶点都在边长为
的三个顶点都在边长为![]() 的小正方形的格点上,关
的小正方形的格点上,关![]() 于
于![]() 轴的对称图形为
轴的对称图形为![]() ,以
,以![]() 与
与![]() 组成一个基本图形,不断复制与平移这个基本图形,得到图形所示的图形
组成一个基本图形,不断复制与平移这个基本图形,得到图形所示的图形
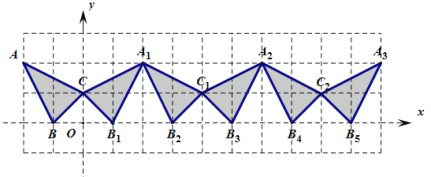
(1)观察以上图形并填写下列各点坐标:
![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() 为正整数)
为正整数)
(2)若![]() 是这组图形中的一个三角形,当
是这组图形中的一个三角形,当![]() 时,则
时,则![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 交
交![]() 轴于
轴于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]()
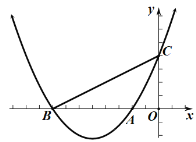
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 若
若![]() 是
是![]() 轴下方抛物线上的一点,且
轴下方抛物线上的一点,且![]() ,请通过计算或推理判断
,请通过计算或推理判断![]() 与
与![]() 的位置关系:
的位置关系:
![]() 在
在![]() 轴左侧的抛物线上是否存在与点
轴左侧的抛物线上是否存在与点![]() 不重合的点
不重合的点![]() ,使
,使![]() 等于
等于![]() 中的某个锐角? 若存在,请求出
中的某个锐角? 若存在,请求出![]() 的值:若不存在,请说明理由.
的值:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,BC=9, CA=12,∠ABC的平分线BD交AC与点D, DE⊥DB交AB于点E.
(1)设⊙O是△BDE的外接圆,求证:AC是⊙O的切线;
(2)设⊙O交BC于点F,连结EF,求![]() 的值.
的值.
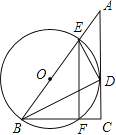
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:若关于x的一元二次方程ax2+bx+c=0的两个非零实数根分别为x1,x2,则x1+x2=﹣![]() ,x1x2=
,x1x2=![]() .
.
解决下列问题:已知关于x的一元二次方程(x+n)2=6x有两个非零不等实数根x1,x2,设m=![]() ,
,
(Ⅰ)当n=1时,求m的值;
(Ⅱ)是否存在这样的n值,使m的值等于![]() ?若存在,求出所有满足条件的n的值;若不存在,请说明理由.
?若存在,求出所有满足条件的n的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
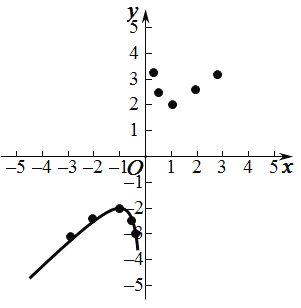
【题目】某“兴趣小组”根据学习函数的经验,对函数y=x+![]() 的图象和性质进行了探究,探究过程如下,请补充完整
的图象和性质进行了探究,探究过程如下,请补充完整
(1)函数y=x+![]() 的自变量取值范围是 .
的自变量取值范围是 .
(2)下表是x与y的几组对应值

则表中m的值为 .
(3)根据表中数据,在如图所示平面直角坐标xOy中描点,并画出函数的一部分,请画出该函数的图象的另一部分,
(4)观察函数图象:写出该函数的一条性质: .
(5)进一步探究发现:函数y=x+![]() 图象与直线y=﹣2只有一交点,所以方程x+
图象与直线y=﹣2只有一交点,所以方程x+![]() =﹣2只有1个实数根,若方程x+
=﹣2只有1个实数根,若方程x+![]() =k(x<0)有两个不相等的实数根,则k的取值范围是 .
=k(x<0)有两个不相等的实数根,则k的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于点C(0,3),其对称轴与
轴交于点C(0,3),其对称轴与![]() 轴交于点A(2,0).
轴交于点A(2,0).
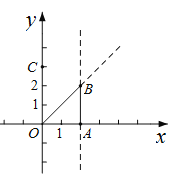
(1)求抛物线![]() 的解析式;
的解析式;
(2)将抛物线![]() 适当平移,使平移后的抛物线
适当平移,使平移后的抛物线![]() 的顶点为D(0,
的顶点为D(0,![]() ).已知点B(2,2),若抛物线
).已知点B(2,2),若抛物线![]() 与△OAB的边界总有两个公共点,请结合函数图象,求
与△OAB的边界总有两个公共点,请结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
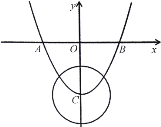
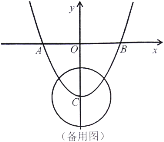
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() 的半径为
的半径为![]() ,
,![]() 为
为![]() 上一动点.
上一动点.
(1)求点![]() ,
,![]() 的坐标?
的坐标?
(2)是否存在点![]() ,使得
,使得![]() 为直角三角形?若存在,求出点
为直角三角形?若存在,求出点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长凝大蒜产于榆次区长凝镇,种植历史悠久,清初曾被选为皇家贡品,在晋中以及省内外享有盛誉.秋天勤劳的农民们将大蒜编成串后进行销售.小乐通过网店推广家乡特产,销售大蒜.每串大蒜的成本是6元,销售一段时间后,发现当售价为每串25元时,平均每天能售出12串.小乐想让更多的人尝到长凝大蒜,因此进行了降价销售,经调查发现,每串大蒜每降价0.5元,平均每天多售出2串.若小乐既想保证平均每天获利420元,又想扩大销售量,那么每串大蒜应降价多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com