
【题目】长凝大蒜产于榆次区长凝镇,种植历史悠久,清初曾被选为皇家贡品,在晋中以及省内外享有盛誉.秋天勤劳的农民们将大蒜编成串后进行销售.小乐通过网店推广家乡特产,销售大蒜.每串大蒜的成本是6元,销售一段时间后,发现当售价为每串25元时,平均每天能售出12串.小乐想让更多的人尝到长凝大蒜,因此进行了降价销售,经调查发现,每串大蒜每降价0.5元,平均每天多售出2串.若小乐既想保证平均每天获利420元,又想扩大销售量,那么每串大蒜应降价多少元?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,使点D恰好落在BC边上的F点处.已知折痕AE=10![]() ,且CE:CF=4:3,那么该矩形的周长为( )
,且CE:CF=4:3,那么该矩形的周长为( )
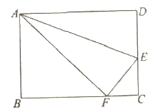
A.48B.64C.92D.96
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=![]() x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.
x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.

A. (-3,0) B. (-6,0) C. (-![]() ,0) D. (-
,0) D. (-![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,设
,设![]() ,
,![]() .
.
(1)如图1,当点![]() 在
在![]() 内,
内,
①若![]() ,求
,求![]() 的度数;
的度数;
小明同学通过分析已知条件发现:![]() 是顶角为
是顶角为![]() 的等腰三角形,且
的等腰三角形,且![]() ,从而容易联想到构造一个顶角为
,从而容易联想到构造一个顶角为![]() 的等腰三角形.于是,他过点
的等腰三角形.于是,他过点![]() 作
作![]() ,且
,且![]() ,连接
,连接![]() ,发现两个不同的三角形全等:______
,发现两个不同的三角形全等:______![]() _______再利用全等三角形及等腰三角形的相关知识可求出
_______再利用全等三角形及等腰三角形的相关知识可求出![]() 的度数
的度数
请利用小王同学分析的思路,通过计算求得![]() 的度数为_____;
的度数为_____;
②小王在①的基础上进一步进行探索,发现![]() 之间存在一种特殊的等量关系,请写出这个等量关系,并加以证明.
之间存在一种特殊的等量关系,请写出这个等量关系,并加以证明.
(2)如图2,点![]() 在
在![]() 外,那么
外,那么![]() 之间的数量关系是否改变?若改变,请直接写出它们的数量关系;若不变,请说明理由.
之间的数量关系是否改变?若改变,请直接写出它们的数量关系;若不变,请说明理由.

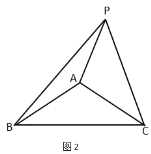
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() ,
,![]() 与
与![]() 相切于点
相切于点![]() ,
,![]() 、
、![]() 是正方形与圆的另两个交点.
是正方形与圆的另两个交点.
(1)![]() __________
__________![]() ,圆心
,圆心![]() 到直线
到直线![]() 的距离为__________;
的距离为__________;
(2)求![]() 的半径长和
的半径长和![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
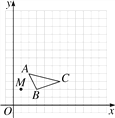
【题目】在13×13的网格图中,已知△ABC和点M(1,2).
(1)以点M为位似中心,画出△ABC的位似图形△A′B′C′,其中△A′B′C′与△ABC的位似比为2;
(2)写出△A′B′C′的各顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
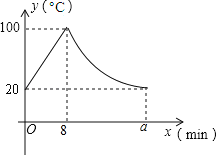
【题目】某小学为每个班级配备了一种可以加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10℃,待加热到100℃,饮水机自动停止加热,水温开始下降,水温y(℃)与通电时间x(min)成反比例关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温为20℃,接通电源后,水温y(℃)与通电时间x(min)的关系如下图所示,回答下列问题:
(1)当0≤x≤8时,求y与x之间的函数关系式;
(2)求出图中a的值;
(3)某天早上7:20,李老师将放满水后的饮水机电源打开,若他想在8:00上课前能喝到不超过40℃的温开水,问:他应在什么时间段内接水?
查看答案和解析>>
科目:初中数学 来源: 题型:
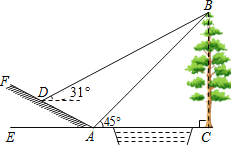
【题目】数学活动课上,小明和小红要测量小河对岸大树BC的高度,小红在点A测得大树顶端B的仰角为45°,小明从A点出发沿斜坡走3![]() 米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2.
米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2.
(1)求小明从点A到点D的过程中,他上升的高度;
(2)依据他们测量的数据能否求出大树BC的高度?若能,请计算;若不能,请说明理由.(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com