
【题目】如图,已知抛物线![]() 交
交![]() 轴于
轴于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]()
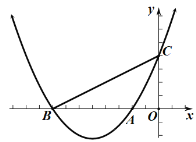
![]() 求抛物线的解析式;
求抛物线的解析式;
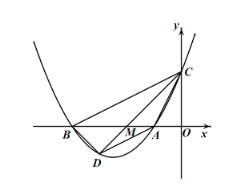
![]() 若
若![]() 是
是![]() 轴下方抛物线上的一点,且
轴下方抛物线上的一点,且![]() ,请通过计算或推理判断
,请通过计算或推理判断![]() 与
与![]() 的位置关系:
的位置关系:
![]() 在
在![]() 轴左侧的抛物线上是否存在与点
轴左侧的抛物线上是否存在与点![]() 不重合的点
不重合的点![]() ,使
,使![]() 等于
等于![]() 中的某个锐角? 若存在,请求出
中的某个锐角? 若存在,请求出![]() 的值:若不存在,请说明理由.
的值:若不存在,请说明理由.
【答案】(1)y= ![]() x2+
x2+![]() +4;(2)AD∥BC;(3)存在满足条件的点P,当∠ACP=∠OBC时,
+4;(2)AD∥BC;(3)存在满足条件的点P,当∠ACP=∠OBC时,![]() =
=![]() ;当∠ACP'=∠OCB时,
;当∠ACP'=∠OCB时,![]() =1
=1
【解析】
(1)设抛物线的解析式为交点式,用待定系数法求解即可.
(2)由![]() ,利用
,利用![]() 轴上的M(-4,0),确定D的坐标,利用
轴上的M(-4,0),确定D的坐标,利用![]() 的解析式确定它们的位置关系.
的解析式确定它们的位置关系.
(3)分情况讨论:①当CP在AC右侧时,显然不存在,
②当CP在AC左侧时,当∠ACP=∠OBC,证明△ACQ∽△ABC可得答案,
再过![]() 作
作![]() ,交抛物线于
,交抛物线于![]() ,利用垂直确定
,利用垂直确定![]() 的坐标,说明∠ACP' =∠OCB,
的坐标,说明∠ACP' =∠OCB,
所以可得答案.
(1)由题设可设抛物线解析式为y=a (x+2)(x+8),
将点C的坐标代入,得4=16a,解得a=![]() ,
,
∴抛物线解析式为y=![]() (x+2)(x+8)=
(x+2)(x+8)=![]() x2+
x2+![]() +4,
+4,
(2)取点M(-4,0),连接CM并延长,交抛物线于点D,则BM=2AM,
故S△CBM=2S△CAM,S△MBD=2S△MAD,∴S△CBD=2S△CAD,
设![]() 为
为![]() ,
,
![]() ,解得:
,解得:![]() ,
,
![]() 直线CD的解析式为y=x+4
直线CD的解析式为y=x+4
由 解得
解得![]() ,
,![]() ,
,
∴D(-6,-2),
同理:lAD:![]() ,lBC:
,lBC:![]() ,
,
∴AD∥BC;
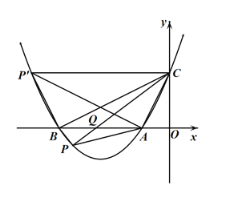
(3)存在
①当CP在AC右侧时,满足∠ACP=∠OBC的CP与抛物线只有一个交点C,与题意不符,
故此时不存在;
②当CP在AC左侧时,设CP交x轴于点Q,
![]()
![]() AC=
AC=![]() ,
,
∵∠ACP=∠OBC,∠CAQ=∠BAC,
∴△ACQ∽△ABC,
∴![]() ,可得AQ=
,可得AQ=![]() ,
,
则AQ:BQ=5:4,
∴![]() =
=![]() ,
,
![]() ,
,
![]() ,
,
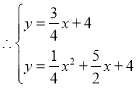 ,解得:
,解得:
此时点P的坐标为(![]() )
)
③![]() ,
,
![]() 为
为![]() ,
,
过![]() 作
作![]() ,交抛物线于
,交抛物线于![]() ,
,
则设:![]() 为
为![]() ,把
,把![]() 代入得:
代入得:![]()
所以:![]() 为
为![]() ,
,
 , 解得:
, 解得:![]()
![]() P' (-10,4),
P' (-10,4),
则由两点间距离公式得:AP' =![]() ,CP' =10,
,CP' =10,
∵AC2+AP' 2=CP' 2,
∴△AP' C为直角三角形,
∵tan∠ACP' =2,tan∠OCB=2,
∴∠ACP' =∠OCB,
此时点P满足条件,
∵AB∥CP',
∴S△CBD=2S△CAD,
∴![]() =1,
=1,
综上,存在满足条件的点P,当∠ACP=∠OBC时,![]() =
=![]() ;
;
当∠ACP'=∠OCB时,![]() =1.
=1.


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图所示的两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
扇形统计图
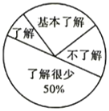
条形统计图

(1)接受问卷调查的学生共有_______人,扇形统计图中“不了解”部分所对应扇形的圆心角度数为_______,并把条形统计图补充完整;
(2)若该中学共有学生![]() 人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为_______人;
人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为_______人;
(3)若从对校园安全知识达到“了解”程度的![]() ,
,![]() ,
,![]()
![]() 个女生和
个女生和![]() ,
,![]()
![]() 个男生中随机抽取
个男生中随机抽取![]() 人参加校园安全知识竞赛,请用画树状图法或列表法求出恰好抽到
人参加校园安全知识竞赛,请用画树状图法或列表法求出恰好抽到![]() 个男生和
个男生和![]() 个女生的概率.
个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图,对称轴是直线x=﹣1,有以下结论:①abc>0;②4ac<b2;③2a﹣b=0;④a﹣b+c>0;⑤9a﹣3b+c>0.其中正确的结论有_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(发现问题)爱好数学的小明在做作业时碰到这样的一道题目:
如图①,点O为坐标原点,⊙O的半径为1,点A(2,0).动点B在⊙O上,连结AB,作等边△ABC(A,B,C为顺时针顺序),求OC的最大值
(解决问题)小明经过多次的尝试与探索,终于得到解题思路:在图①中,连接OB,以OB为边在OB的左侧作等边三角形BOE,连接AE.
(1)请你找出图中与OC相等的线段,并说明理由;
(2)求线段OC的最大值.
(灵活运用)
(3)如图②,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,求线段AM长的最大值及此时点P的坐标.
(迁移拓展)
(4)如图③,BC=4![]() ,点D是以BC为直径的半圆上不同于B、C的一个动点,以BD为边作等边△ABD,请直接写出AC的最值.
,点D是以BC为直径的半圆上不同于B、C的一个动点,以BD为边作等边△ABD,请直接写出AC的最值.

查看答案和解析>>
科目:初中数学 来源: 题型:
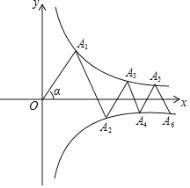
【题目】如图,点A1、A3、A5…在反比例函数y=![]() (x>0)的图象上,点A2、A4、A6……在反比例函数y=-
(x>0)的图象上,点A2、A4、A6……在反比例函数y=-![]() (x>0)的图象上,∠OA1A2=∠A1A2A3=∠A2A3A4=…=∠α=60°,且OA1=2,则An(n为正整数)的纵坐标为________________________________.(用含n的式子表示)
(x>0)的图象上,∠OA1A2=∠A1A2A3=∠A2A3A4=…=∠α=60°,且OA1=2,则An(n为正整数)的纵坐标为________________________________.(用含n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,使点D恰好落在BC边上的F点处.已知折痕AE=10![]() ,且CE:CF=4:3,那么该矩形的周长为( )
,且CE:CF=4:3,那么该矩形的周长为( )
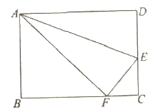
A.48B.64C.92D.96
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=![]() x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.
x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.

A. (-3,0) B. (-6,0) C. (-![]() ,0) D. (-
,0) D. (-![]() ,0)
,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com