
【题目】二次函数y=ax2+bx+c的图象如图,对称轴是直线x=﹣1,有以下结论:①abc>0;②4ac<b2;③2a﹣b=0;④a﹣b+c>0;⑤9a﹣3b+c>0.其中正确的结论有_____.

【答案】①②③④
【解析】
根据抛物线的开口方向、与y轴的交点和对称轴即可求出a、b、c的符号,从而判断①;然后根据抛物线与x轴的交点个数即可判断②;根据抛物线对称轴公式即可判断③;根据当x=-1时,y>0,代入即可判断④;利用抛物线的对称性可得当x=﹣3时,y<0,然后代入即可判断⑤.
解:由图象可知:a<0,c>0,
又∵对称轴是直线x=﹣1,
∴根据对称轴在y轴左侧,a,b同号,可得b<0,
∴abc>0,
故①正确;
∵抛物线与x轴有两个交点,
∴△=b2﹣4ac>0,
∴4ac<b2,
故②正确;
∵对称轴是直线x=﹣1,
∴﹣![]() =﹣1,
=﹣1,
∴b=2a,
∴2a﹣b=0,
故③正确;
∵当x=﹣1时,y>0,
∴a﹣b+c>0,
故④正确;
∵对称轴是直线x=﹣1,且由图象可得:当x=1时,y<0,
∴当x=﹣3时,y<0,
∴9a﹣3b+c<0,
故⑤错误.
综上,正确的有①②③④.
故答案为:①②③④.


科目:初中数学 来源: 题型:
【题目】对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了调查同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取部分同学进行问卷测试,把测试成绩分成“优、良、中、差”四个等级,绘制了如下不完整的统计图:

根据以上统计信息,解答下列问题:
(1)求成绩是“优”的人数占抽取人数的百分比;
(2)求本次随机抽取问卷测试的人数;
(3)请把条形统计图补充完整;
(4)若该校学生人数为3000人,请估计成绩是“优”和“良”的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图像如图所示,对称轴为直线
的图像如图所示,对称轴为直线![]() ,则下列结论正确的有( )
,则下列结论正确的有( )
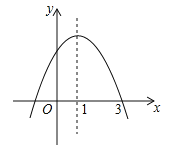
①![]() ;②方程
;②方程![]() 的两个根是
的两个根是![]() ,
,![]() ;
;
③![]() ;④当
;④当![]() 时,
时,![]() 随
随![]() 的增大而减小.
的增大而减小.
A.①②B.②③C.①④D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,![]() 的三个顶点都在边长为
的三个顶点都在边长为![]() 的小正方形的格点上,关
的小正方形的格点上,关![]() 于
于![]() 轴的对称图形为
轴的对称图形为![]() ,以
,以![]() 与
与![]() 组成一个基本图形,不断复制与平移这个基本图形,得到图形所示的图形
组成一个基本图形,不断复制与平移这个基本图形,得到图形所示的图形
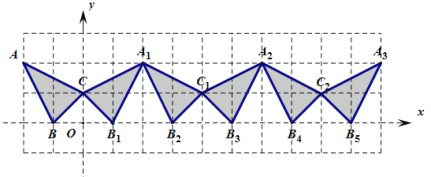
(1)观察以上图形并填写下列各点坐标:
![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() 为正整数)
为正整数)
(2)若![]() 是这组图形中的一个三角形,当
是这组图形中的一个三角形,当![]() 时,则
时,则![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
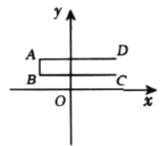
【题目】如图,已知点![]() ,
,![]() ,
,![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,![]() ,
,![]() .线段
.线段![]() ,
,![]() ,
,![]() 组成的图形为图形
组成的图形为图形![]() ,点
,点![]() 沿
沿![]() 移动,设点
移动,设点![]() 移动的距离为
移动的距离为![]() ,直线
,直线![]() 过点
过点![]() ,且在点
,且在点![]() 移动过程中,直线
移动过程中,直线![]() 随
随![]() 运动而运动.
运动而运动.
(1)若点![]() 过点
过点![]() 时,求直线
时,求直线![]() 的解析式;
的解析式;
(2)当![]() 过点
过点![]() 时,求
时,求![]() 值;
值;
(3)①若直线![]() 与图形
与图形![]() 有一个交点,直接写出
有一个交点,直接写出![]() 的取值范围;
的取值范围;
②若直线![]() 与图形
与图形![]() 有两个交点,直接写出
有两个交点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
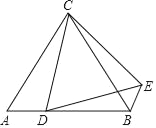
【题目】如图,△ABC是边长为4的等边三角形,点D是AB上异于A,B的一动点,将△ACD绕点C逆时针旋转60°得△BCE,则旋转过程中△BDE周长的最小值_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】铁岭市某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量y(千克)与每千克降价x(元)(0<x<20)之间满足一次函数关系,其图象如图所示:
(1)求y与x之间的函数关系式;
(2)商贸公司要想获利2090元,则这种干果每千克应降价多少元?
(3)该干果每千克降价多少元时,商贸公司获利最大?最大利润是多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 交
交![]() 轴于
轴于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]()
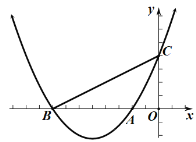
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 若
若![]() 是
是![]() 轴下方抛物线上的一点,且
轴下方抛物线上的一点,且![]() ,请通过计算或推理判断
,请通过计算或推理判断![]() 与
与![]() 的位置关系:
的位置关系:
![]() 在
在![]() 轴左侧的抛物线上是否存在与点
轴左侧的抛物线上是否存在与点![]() 不重合的点
不重合的点![]() ,使
,使![]() 等于
等于![]() 中的某个锐角? 若存在,请求出
中的某个锐角? 若存在,请求出![]() 的值:若不存在,请说明理由.
的值:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于点C(0,3),其对称轴与
轴交于点C(0,3),其对称轴与![]() 轴交于点A(2,0).
轴交于点A(2,0).
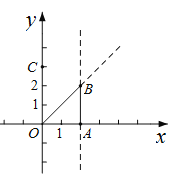
(1)求抛物线![]() 的解析式;
的解析式;
(2)将抛物线![]() 适当平移,使平移后的抛物线
适当平移,使平移后的抛物线![]() 的顶点为D(0,
的顶点为D(0,![]() ).已知点B(2,2),若抛物线
).已知点B(2,2),若抛物线![]() 与△OAB的边界总有两个公共点,请结合函数图象,求
与△OAB的边界总有两个公共点,请结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com