
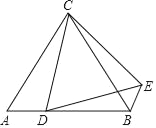
【题目】如图,△ABC是边长为4的等边三角形,点D是AB上异于A,B的一动点,将△ACD绕点C逆时针旋转60°得△BCE,则旋转过程中△BDE周长的最小值_____
【答案】2![]() +4.
+4.
【解析】
由旋转的性质得到BE=AD,于是得到C△DBE=BE+DB+DE=AB+DE=4+DE,根据等边三角形的性质得到DE=CD,由垂线段最短得到当CD⊥AB时,△BDE的周长最小,于是得到结论.
∵将△ACD绕点C逆时针方向旋转60°得到△BCE,
∴∠DCE=60°,DC=EC,
∴△CDE是等边三角形,
由旋转的性质得,BE=AD,
∴C△DBE=BE+DB+DE=AB+DE=4+DE,
∵△CDE是等边三角形,
∴DE=CD,
∴C△DBE=CD+4,
由垂线段最短可知,当CD⊥AB时,△BDE的周长最小,
此时,CD=2![]() ,
,
∴△BDE的最小周长=CD+4=2![]() +4,
+4,
故答案为:2![]() +4.
+4.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】远远在一个不透明的盒子里装了4个除颜色外其他都相同的小球,其中有3个是红球,1个是绿球,每次拿一个球然后放回去,拿2次,则至少有一次取到绿球的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴相交于点C(0,3),且
轴相交于点C(0,3),且![]() ,
,![]() ,抛物线的顶点为
,抛物线的顶点为![]() .
.
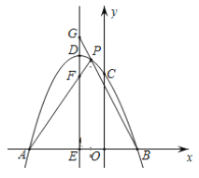
(1)求![]() 、
、![]() 两点的坐标.
两点的坐标.
(2)求抛物线的表达式.
(3)过点![]() 作直线
作直线![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,点
,点![]() 是抛物线上
是抛物线上![]() ,
,![]() 两点间的一个动点(点
两点间的一个动点(点![]() 不与
不与![]() 、
、![]() 两点重合),
两点重合),![]() 、
、![]() 与直线
与直线![]() 分别相交于点
分别相交于点![]() 、
、![]() 当点
当点![]() 运动时,
运动时,![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图,对称轴是直线x=﹣1,有以下结论:①abc>0;②4ac<b2;③2a﹣b=0;④a﹣b+c>0;⑤9a﹣3b+c>0.其中正确的结论有_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
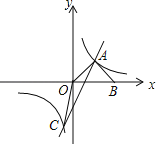
【题目】如图,在平面直角坐标系中,直线y1=2x﹣2与双曲线y2=![]() 交于A、C两点,AB⊥OA交x轴于点B,且AB=OA.
交于A、C两点,AB⊥OA交x轴于点B,且AB=OA.
(1)求双曲线的解析式;
(2)连接OC,求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系 xOy 中,直线 l:![]() 与 x 轴交于点 A(-2,0),与 y 轴交于点 B.双曲线
与 x 轴交于点 A(-2,0),与 y 轴交于点 B.双曲线![]() 与直线 l 交于 P,Q 两点,其中点 P 的纵坐标大于点 Q 的纵坐标.
与直线 l 交于 P,Q 两点,其中点 P 的纵坐标大于点 Q 的纵坐标.
(1)求点 B 的坐标;
(2)当点 P 的横坐标为 2 时,求 k 的值;
(3)连接 PO,记△POB 的面积为 S,若![]() ,直接写出 k 的取值范围.
,直接写出 k 的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com