
����Ŀ�����������⣩������ѧ��С��������ҵʱ����������һ����Ŀ��
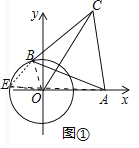
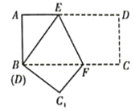
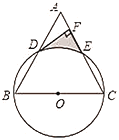
��ͼ�٣���OΪ����ԭ�㣬��O�İ뾶Ϊ1����A��2��0��������B�ڡ�O�ϣ�����AB�����ȱߡ�ABC��A��B��CΪ˳ʱ��˳����OC�����ֵ
��������⣩С��������εij�����̽�������ڵõ�����˼·����ͼ���У�����OB����OBΪ����OB��������ȱ�������BOE������AE��
��1�������ҳ�ͼ����OC��ȵ��߶Σ���˵�����ɣ�
��2�����߶�OC�����ֵ��
��������ã�
��3����ͼ�ڣ���ƽ��ֱ������ϵ�У���A������Ϊ��2��0������B������Ϊ��5��0������PΪ�߶�AB��һ���㣬��PA��2��PM��PB����BPM��90�㣬���߶�AM�������ֵ����ʱ��P�����꣮
��Ǩ����չ��
��4����ͼ�ۣ�BC��4![]() ����D����BCΪֱ���İ�Բ�ϲ�ͬ��B��C��һ�����㣬��BDΪ�����ȱߡ�ABD����ֱ��д��AC����ֵ��
����D����BCΪֱ���İ�Բ�ϲ�ͬ��B��C��һ�����㣬��BDΪ�����ȱߡ�ABD����ֱ��д��AC����ֵ��

���𰸡���1�����ۣ�OC��AE�����ɼ���������2��OC�����ֵΪ3����3�����ֵΪ2![]() +3��P��2��
+3��P��2��![]() ��
��![]() ������4��AC�����ֵΪ2
������4��AC�����ֵΪ2![]() +2
+2![]() �� 2
�� 2![]() ��2
��2![]() ��
��
��������
��1�����ۣ�![]() ��ֻҪ֤��
��ֻҪ֤��![]() ���ɣ�
���ɣ�
��2�����������ε����߹�ϵ���ɽ�����⣻
��3������![]() ����
����![]() ���ŵ�
���ŵ�![]() ˳ʱ����ת
˳ʱ����ת![]() �õ�
�õ�![]() ������
������![]() ���õ�
���õ�![]() �ǵ���ֱ�������Σ�����ȫ�������ε����ʵõ�
�ǵ���ֱ�������Σ�����ȫ�������ε����ʵõ�![]() ��
��![]() �����ݵ�
�����ݵ�![]() ���߶�
���߶�![]() ���ӳ���ʱ���߶�
���ӳ���ʱ���߶�![]() ȡ�����ֵ�����ɵõ����ֵΪ
ȡ�����ֵ�����ɵõ����ֵΪ![]() ����
����![]() ��
��![]() ����
����![]() �����ݵ���ֱ�������ε����ʣ����ɵõ����ۣ�
�����ݵ���ֱ�������ε����ʣ����ɵõ����ۣ�
��4����ͼ4�У���![]() Ϊ�����ȱ�������
Ϊ�����ȱ�������![]() ����
����![]() ���Ƴ�
���Ƴ�![]() ���Ƴ�����
���Ƴ�����![]() �����ֵ��ֻҪ���
�����ֵ��ֻҪ���![]() �����ֵ���ɣ���
�����ֵ���ɣ���![]() ��ֵ��
��ֵ��![]() ���Ƴ���
���Ƴ���![]() ����
����![]() Ϊֱ����
Ϊֱ����![]() ���˶�����ͼ���֪������
���˶�����ͼ���֪������![]() ��
��![]() �Ϸ���
�Ϸ���![]() ʱ��
ʱ��![]() ��ֵ���.
��ֵ���.
��1����ͼ���У����ۣ�OC��AE��
���ɣ��ߡ�ABC����BOE���ǵȱ������Σ�
��BC��BA��BO��BE����CBA����OBE��60�㣬
���CBO����ABE��
���CBO�ա�ABE��
��OC��AE��
��2���ڡ�AOE�У�AE��OE+OA��
�൱E��O��A���ߣ�
��AE�����ֵΪ3��
��OC�����ֵΪ3��
��3����ͼ1������BM��
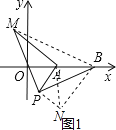
�߽���APM���ŵ�P˳ʱ����ת90��õ���PBN������AN�����APN�ǵ���ֱ�������Σ�
��PN��PA��2��BN��AM��
��A��������2��0������B��������5��0����
��OA��2��OB��5��
��AB��3��
���߶�AM�������ֵ���߶�BN�������ֵ��
�൱N���߶�BA���ӳ���ʱ���߶�BNȡ�����ֵ����ͼ2�У�
���ֵ��AB+AN��
��AN��![]() AP��2
AP��2![]() ��
��
�����ֵΪ2![]() +3��
+3��
��ͼ2����P��PE��x����E��
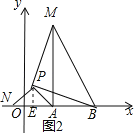
�ߡ�APN�ǵ���ֱ�������Σ�
��PE��AE��![]() ��
��
��OE��BO��AB��AE��5��3��![]() ��2��
��2��![]() ��
��
��P��2��![]() ��
��![]() ����
����
��4����ͼ4�У���BCΪ�����ȱ������Ρ�BCM��
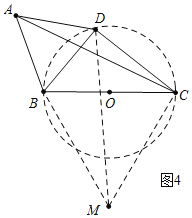
�ߡ�ABD����CBM��60�㣬
���ABC����DBM����AB��DB��BC��BM��
���ABC�ա�DBM��
��AC��MD��
������AC�����ֵ��ֻҪ���DM�����ֵ���ɣ�
��BC��4![]() ����ֵ����BDC��90�㣬
����ֵ����BDC��90�㣬
���D����BCΪֱ���ġ�O���˶���
��ͼ���֪������D��BC�Ϸ���DM��BCʱ��DM��ֵ������ֵ��2![]() +2
+2![]() ��
��
��AC�����ֵΪ2![]() +2
+2![]() ��
��
����A���߶�BD���Ҳ�ʱ��ͬ���ɵ�AC����СֵΪ2![]() ��2
��2![]() ��
��


 ���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ֽƬ![]() �۵���ʹ��
�۵���ʹ��![]() ���
���![]() �غϣ���
�غϣ���![]() ����
����![]() �����ۺ�Ϊ
�����ۺ�Ϊ![]() ����
����![]() ��
��![]() �����߶�
�����߶�![]() �ij���Ϊ________��
�ij���Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��![]() ��
��![]() ��
��![]() ��
��![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ���߶�
���߶�![]() ��
��![]() ��
��![]() ��ɵ�ͼ��Ϊͼ��
��ɵ�ͼ��Ϊͼ��![]() ����
����![]() ��
��![]() �ƶ������
�ƶ������![]() �ƶ��ľ���Ϊ
�ƶ��ľ���Ϊ![]() ��ֱ��
��ֱ��![]() ����
����![]() �����ڵ�
�����ڵ�![]() �ƶ������У�ֱ��
�ƶ������У�ֱ��![]() ��
��![]() �˶����˶���
�˶����˶���
��1������![]() ����
����![]() ʱ����ֱ��
ʱ����ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����![]() ����
����![]() ʱ����
ʱ����![]() ֵ��
ֵ��
��3������ֱ��![]() ��ͼ��
��ͼ��![]() ��һ�����㣬ֱ��д��
��һ�����㣬ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
����ֱ��![]() ��ͼ��
��ͼ��![]() ���������㣬ֱ��д��
���������㣬ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
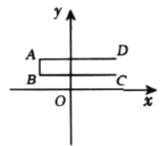
����Ŀ��������ij��ó��˾��ÿǧ��40Ԫ�ļ۸�һ�ָɹ����ƻ���ÿǧ��60Ԫ�ļ۸����ۣ�Ϊ���ù˿͵õ������ʵ�ݣ��־����������ۣ���֪���ָɹ�������y(ǧ��)��ÿǧ�˽���x(Ԫ)(0��x��20)֮������һ�κ�����ϵ����ͼ����ͼ��ʾ��
(1)��y��x֮��ĺ�����ϵʽ��
(2)��ó��˾Ҫ�����2090Ԫ�������ָɹ�ÿǧ��Ӧ���۶���Ԫ��
(3)�øɹ�ÿǧ�˽��۶���Ԫʱ����ó��˾���������������Ƕ���Ԫ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����л���ͳ�Ļ���ǭ���ݽ��ھٰ�����Сѧ������ѧ�����������������ĿΪ��A����ʫ��B���δʣ�C�����D�����־���������ʽ����������������˫��������
��1��С���μ������������������������ȡһ��������Ŀ��ǡ�ó��������־����ĸ����Ƕ��٣�
��2��С���С�����һ��С��μ���˫���������������������ǣ�ͬһС���������Ա�ı�����Ŀ������ͬ����ÿ��ֻ�������ȡһ�Σ���ǡ��С���������ʫ����С���������δ����ĸ����Ƕ��٣����û���״ͼ���б��ķ�������˵����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() ��
��![]() ����
����![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() ������
������![]()
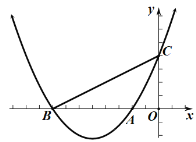
![]() �������ߵĽ���ʽ;
�������ߵĽ���ʽ;
![]() ��
��![]() ��
��![]() ���·��������ϵ�һ�㣬��
���·��������ϵ�һ�㣬��![]() ����ͨ������������ж�
����ͨ������������ж�![]() ��
��![]() ��λ�ù�ϵ:
��λ�ù�ϵ:
![]() ��
��![]() ���������������Ƿ�������
���������������Ƿ�������![]() ���غϵĵ�
���غϵĵ�![]() ��ʹ
��ʹ![]() ����
����![]() �е�ij�����? �����ڣ������
�е�ij�����? �����ڣ������![]() ��ֵ:�������ڣ���˵�����ɣ�
��ֵ:�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() �ֱ�x�ᡢy���ڵ�B��C��������AOCD�Ķ���D�ڵڶ������ڣ�E��BC�е㣬OF��DE�ڵ�F������OE������P��AO�ϴӵ�A���յ�O�����˶���ͬʱ������Q��ֱ��BC�ϴ�ij��Q1���յ�Q2�����˶�������ͬʱ�����յ㣮
�ֱ�x�ᡢy���ڵ�B��C��������AOCD�Ķ���D�ڵڶ������ڣ�E��BC�е㣬OF��DE�ڵ�F������OE������P��AO�ϴӵ�A���յ�O�����˶���ͬʱ������Q��ֱ��BC�ϴ�ij��Q1���յ�Q2�����˶�������ͬʱ�����յ㣮
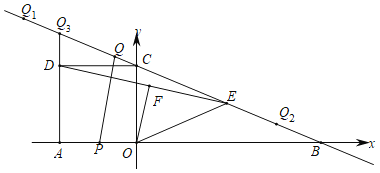
��1�����B�������OE�ij���
��2�����Q2Ϊ(m��n)����![]() tan��EOFʱ�����Q2�����ꣻ
tan��EOFʱ�����Q2�����ꣻ
��3�����ݣ�2��������������P�˶���AO�е�ʱ����Qǡ�����C�غϣ�
���ӳ�AD��ֱ��BC�ڵ�Q3������Q���߶�Q2Q3��ʱ����Q3Q��s��AP��t����s����t�ĺ�������ʽ��
�ڵ�PQ���OEF��һ��ƽ��ʱ������������������AP�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ�������x��һԪ���η���ax2+bx+c��0����������ʵ�����ֱ�Ϊx1��x2����x1+x2����![]() ��x1x2��
��x1x2��![]() .
.
����������⣺��֪����x��һԪ���η���(x+n)2��6x���������㲻��ʵ����x1��x2����m��![]() ��
��
(��)��n��1ʱ����m��ֵ��
(��)�Ƿ����������nֵ��ʹm��ֵ����![]() �������ڣ������������������n��ֵ���������ڣ���˵������.
�������ڣ������������������n��ֵ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���Եȱ�![]() �ı�
�ı�![]() Ϊֱ����
Ϊֱ����![]() ���ֱ�
���ֱ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
��1����֤��![]() ��
��![]() �����ߣ�
�����ߣ�
��2�����ȱ�![]() �ı߳�Ϊ8������
�ı߳�Ϊ8������![]() ��
��![]() ��
��![]() Χ�ɵ���Ӱ���������
Χ�ɵ���Ӱ���������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com