
【题目】已知:如图,以等边![]() 的边
的边![]() 为直径作
为直径作![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
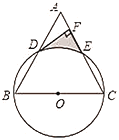
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若等边![]() 的边长为8,求由
的边长为8,求由![]() 、
、![]() 、
、![]() 围成的阴影部分面积.
围成的阴影部分面积.
【答案】(1)详见解析;(2)6![]() ﹣
﹣![]() .
.
【解析】
(1)连接CD、OD,先利用等腰三角形的性质证AD=BD,再证OD为△ABC的中位线得DO∥AC,根据DF⊥AC可得结论;
(2)连接OE,作OG⊥AC,求出EF、DF的长及∠DOE的度数,根据S阴影=S梯形EFDO﹣S扇形DOE计算可得.
解:(1)连接CD、OD,
∵BC是⊙O的直径,
∴∠CDB=90°,即CD⊥AB,
又∵△ABC是等边三角形,
∴AD=BD,
∵BO=CO,
∴DO是△ABC的中位线,
∴OD∥AC,
∵DF⊥AC,
∴DF⊥OD,
∴DF是⊙O的切线;
(2)连接OE,作OG⊥AC于点G,
∴∠OGF=∠DFG=∠ODF=90°,
∴四边形OGFD是矩形,
∴FG=OD=4,
∵OC=OE=OD=OB,且∠ACB=∠B=60°,
∴△OBD和△OCE均为等边三角形,
∴∠BOD=∠COE=60°,CE=OC=4,
∴EG=![]() CE=2,DF=OG=OCsin60°=2
CE=2,DF=OG=OCsin60°=2![]() ,∠DOE=60°,
,∠DOE=60°,
∴EF=FG﹣EG=2,
∴S阴影=S梯形EFDO﹣S扇形DOE=![]() ×(2+4)×2
×(2+4)×2![]() ﹣
﹣![]() =6
=6![]() ﹣
﹣![]() .
.



 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】(发现问题)爱好数学的小明在做作业时碰到这样的一道题目:
如图①,点O为坐标原点,⊙O的半径为1,点A(2,0).动点B在⊙O上,连结AB,作等边△ABC(A,B,C为顺时针顺序),求OC的最大值
(解决问题)小明经过多次的尝试与探索,终于得到解题思路:在图①中,连接OB,以OB为边在OB的左侧作等边三角形BOE,连接AE.
(1)请你找出图中与OC相等的线段,并说明理由;
(2)求线段OC的最大值.
(灵活运用)
(3)如图②,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,求线段AM长的最大值及此时点P的坐标.
(迁移拓展)
(4)如图③,BC=4![]() ,点D是以BC为直径的半圆上不同于B、C的一个动点,以BD为边作等边△ABD,请直接写出AC的最值.
,点D是以BC为直径的半圆上不同于B、C的一个动点,以BD为边作等边△ABD,请直接写出AC的最值.

查看答案和解析>>
科目:初中数学 来源: 题型:
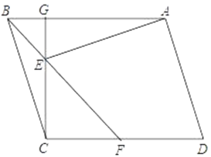
【题目】如图,在ABCD中,CG⊥AB于点G,∠ABF=45°,F在CD上,BF交CG于点E,连接AE,且AE⊥AD.
(1)若BG=2,BC=![]() ,求EF的长度;
,求EF的长度;
(2)求证:CE+![]() BE=AB.
BE=AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC=BC,点G为AC中点,连结BG,CE⊥BG于F,交AB于E,连接GE,点H为AB中点,连接FH.以下结论:(1)∠ACE=∠ABG;(2)∠AGE=∠CGB:(3)若AB=10![]() ,则BF=4
,则BF=4![]() ;(4)FH平分∠BFE;(5)S△BGC=3S△CGE.其中正确结论的个数是( )
;(4)FH平分∠BFE;(5)S△BGC=3S△CGE.其中正确结论的个数是( )
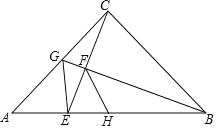
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①![]() ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )

A. ①②③④ B. ①④ C. ②③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=![]() x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.
x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.

A. (-3,0) B. (-6,0) C. (-![]() ,0) D. (-
,0) D. (-![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校共有200名学生,为了解本学期学生参加公益劳动的情况,收集了他们参加公益劳动时间(单位:小时)等数据,以下是根据数据绘制的统计图表的一部分.
学 生 类 型 人数 时间 |
|
|
|
|
| |
性别 | 男 | 7 | 31 | 25 | 30 | 4 |
女 | 8 | 29 | 26 | 32 | 8 | |
学段 | 初中 | 25 | 36 | 44 | 11 | |
高中 | ||||||

下面有四个推断:
①这200名学生参加公益劳动时间的平均数一定在24.5-25.5之间
②这200名学生参加公益劳动时间的中位数在20-30之间
③这200名学生中的初中生参加公益劳动时间的中位数一定在20-30之间
④这200名学生中的高中生参加公益劳动时间的中位数可能在20-30之间
所有合理推断的序号是( )
A. ①③B. ②④C. ①②③D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() ,
,![]() 与
与![]() 相切于点
相切于点![]() ,
,![]() 、
、![]() 是正方形与圆的另两个交点.
是正方形与圆的另两个交点.
(1)![]() __________
__________![]() ,圆心
,圆心![]() 到直线
到直线![]() 的距离为__________;
的距离为__________;
(2)求![]() 的半径长和
的半径长和![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象经过点
的图象经过点![]() .
.
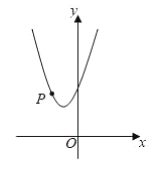
(1)求![]() 的值和图象的顶点坐标;
的值和图象的顶点坐标;
(2)点![]() 在该二次函数图象上.
在该二次函数图象上.
①当![]() 时,求
时,求![]() 的值;
的值;
②若点![]() 到
到![]() 轴的距离小于2,请根据图象直接写出
轴的距离小于2,请根据图象直接写出![]() 的取值范围;
的取值范围;
③直接写出点![]() 与直线
与直线![]() 的距离小于
的距离小于![]() 时
时![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com