
【题目】如图,在![]() 中,
中,![]() ,顶点
,顶点![]() 在
在![]() 轴上,顶点
轴上,顶点![]() 在反比例函数
在反比例函数![]() 的图象上,已知点
的图象上,已知点![]() 的纵坐标是 3,则经过点
的纵坐标是 3,则经过点![]() 的反比例函数的解析式为_____________
的反比例函数的解析式为_____________
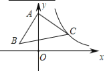
【答案】![]()
【解析】
过C作CD⊥y轴于D,过B作BE⊥y轴于E,即可得到△ABE≌△CAD,依据全等三角形的性质以及点C的坐标,即可得到点B的坐标,进而得出经过点B的反比例函数的解析式.
如图所示,过C作CD⊥y轴于D,过B作BE⊥y轴于E,则∠CDA=∠AEB=90°,
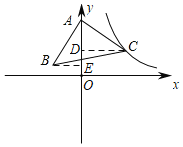
又∵∠BAC=90°,
∴∠BAE+∠CAD=∠ACD+∠CAD=90°,
∴∠BAE=∠ACD,
又∵AB=CA,
∴△ABE≌△CAD(AAS),
又∵顶点C在反比例函数![]()
的图象上,点C的纵坐标为3,
∴点C的横坐标为4,
∴CD=4=AE,OD=3,
∴Rt△ACD中,AD= ![]()
= ![]() =2,
=2,
∴BE=AD=2,AO=AD+DO=2+3=5,
∴OE=AO-AE=5-4=1,
∴B(-2,1),
∴经过点B的反比例函数的解析式为![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系 xOy 中,直线 l:![]() 与 x 轴交于点 A(-2,0),与 y 轴交于点 B.双曲线
与 x 轴交于点 A(-2,0),与 y 轴交于点 B.双曲线![]() 与直线 l 交于 P,Q 两点,其中点 P 的纵坐标大于点 Q 的纵坐标.
与直线 l 交于 P,Q 两点,其中点 P 的纵坐标大于点 Q 的纵坐标.
(1)求点 B 的坐标;
(2)当点 P 的横坐标为 2 时,求 k 的值;
(3)连接 PO,记△POB 的面积为 S,若![]() ,直接写出 k 的取值范围.
,直接写出 k 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,设
,设![]() ,
,![]() .
.
(1)如图1,当点![]() 在
在![]() 内,
内,
①若![]() ,求
,求![]() 的度数;
的度数;
小明同学通过分析已知条件发现:![]() 是顶角为
是顶角为![]() 的等腰三角形,且
的等腰三角形,且![]() ,从而容易联想到构造一个顶角为
,从而容易联想到构造一个顶角为![]() 的等腰三角形.于是,他过点
的等腰三角形.于是,他过点![]() 作
作![]() ,且
,且![]() ,连接
,连接![]() ,发现两个不同的三角形全等:______
,发现两个不同的三角形全等:______![]() _______再利用全等三角形及等腰三角形的相关知识可求出
_______再利用全等三角形及等腰三角形的相关知识可求出![]() 的度数
的度数
请利用小王同学分析的思路,通过计算求得![]() 的度数为_____;
的度数为_____;
②小王在①的基础上进一步进行探索,发现![]() 之间存在一种特殊的等量关系,请写出这个等量关系,并加以证明.
之间存在一种特殊的等量关系,请写出这个等量关系,并加以证明.
(2)如图2,点![]() 在
在![]() 外,那么
外,那么![]() 之间的数量关系是否改变?若改变,请直接写出它们的数量关系;若不变,请说明理由.
之间的数量关系是否改变?若改变,请直接写出它们的数量关系;若不变,请说明理由.

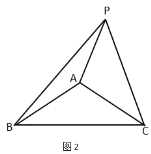
查看答案和解析>>
科目:初中数学 来源: 题型:
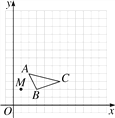
【题目】在13×13的网格图中,已知△ABC和点M(1,2).
(1)以点M为位似中心,画出△ABC的位似图形△A′B′C′,其中△A′B′C′与△ABC的位似比为2;
(2)写出△A′B′C′的各顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
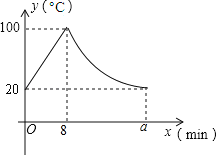
【题目】某小学为每个班级配备了一种可以加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10℃,待加热到100℃,饮水机自动停止加热,水温开始下降,水温y(℃)与通电时间x(min)成反比例关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温为20℃,接通电源后,水温y(℃)与通电时间x(min)的关系如下图所示,回答下列问题:
(1)当0≤x≤8时,求y与x之间的函数关系式;
(2)求出图中a的值;
(3)某天早上7:20,李老师将放满水后的饮水机电源打开,若他想在8:00上课前能喝到不超过40℃的温开水,问:他应在什么时间段内接水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)模型探究:如图1,![]() 、
、![]() 、
、![]() 分别为
分别为![]() 三边
三边![]() 、
、![]() 、
、![]() 上的点,且
上的点,且![]() ,
,![]() 与
与![]() 相似吗?请说明理由.
相似吗?请说明理由.

(2)模型应用:![]() 为等边三角形,其边长为
为等边三角形,其边长为![]() ,
,![]() 为边
为边![]() 上一点,
上一点,![]() 为射线
为射线![]() 上一点,将
上一点,将![]() 沿
沿![]() 翻折,使点
翻折,使点![]() 落在射线
落在射线![]() 上的点
上的点![]() 处,且
处,且![]() .
.
①如图2,当点![]() 在线段
在线段![]() 上时,求
上时,求![]() 的值;
的值;

②如图3,当点![]() 落在线段
落在线段![]() 的延长线上时,求
的延长线上时,求![]() 与
与![]() 的周长之比.
的周长之比.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=3,矩形内部有一动点P满足S△PAB=![]() S矩形ABCD,则点P到A、B两点的距离之和PA+PB的最小值为______.
S矩形ABCD,则点P到A、B两点的距离之和PA+PB的最小值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC 中,AB=AC,点 M 在 BA 的延长线上,点 N 在 BC 的延长线上,过点 C 作CD∥AB 交∠CAM 的平分线于点 D.
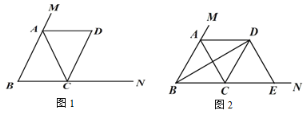
(1)如图 1,求证:四边形 ABCD 是平行四边形;
(2)如图 2,当∠ABC=60°时,连接 BD,过点 D 作 DE⊥BD,交 BN 于点 E,在不添加任何辅助线的情况下,请直接写出图 2 中四个三角形(不包含△CDE),使写出的每个三角形的面积与△CDE 的面积相等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com