
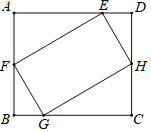
【题目】如图,矩形![]() 的四个顶点分别在矩形
的四个顶点分别在矩形![]() 的各条边上,
的各条边上,![]() ,
,![]() ,
,![]() .有以下四个结论:①
.有以下四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④矩形
;④矩形![]() 的面积是
的面积是![]() .其中正确的结论为( )
.其中正确的结论为( )
A.①②B.①②③C.①②④D.①②③④
【答案】C
【解析】
根据矩形的性质和余角的性质可判定①;根据AAS可判定△BFG≌△DHE,即可判定②,证明△BFG∽△CGH,设GH=EF=a,得出BF,AF,CH,利用勾股定理求出a值,得到BF,再利用勾股定理求出BG=1,可得tan∠BFG,可判定③,计算出矩形EFGH的面积,可判定④.
解:∵∠FGH=90°,
∴∠BGF+∠CGH=90°,
又∵∠CGH+∠CHG=90°,
∴∠BGF=∠CHG,故①正确;
同理可得∠DEH=∠CHG,
∴∠BGF=∠DEH,
又∵∠B=∠D=90°,FG=EH,
在△BFG和△DHE中,
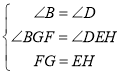 ,
,
∴△BFG≌△DHE(AAS),故②正确;
同理可得△AFE≌△CHG,
∴AF=CH,
由∠BGF=∠CHG,∠B=∠C=90°,
可得△BFG∽△CGH,
设GH=EF=a,
∴![]() ,
,
∴![]() ,
,
∴BF=![]() ,
,
∴AF=AB-BF=a-![]() ,
,
∴CH=AF= a-![]() ,
,
在Rt△CGH中,
∵CG2+CH2=GH2,
∴42+(a-![]() )2=a2,解得a=
)2=a2,解得a=![]() 或
或![]() (舍),
(舍),
∴GH=![]() ,
,
∴BF=![]() =
=![]() ,
,
在Rt△BFG中,
BG=![]() ,
,
∴tan∠BFG=![]() =
=![]() ,故③错误;
,故③错误;
矩形EFGH的面积=FG×GH=3×![]() =
=![]() ,故④正确.
,故④正确.
故选C.


科目:初中数学 来源: 题型:
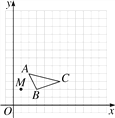
【题目】在13×13的网格图中,已知△ABC和点M(1,2).
(1)以点M为位似中心,画出△ABC的位似图形△A′B′C′,其中△A′B′C′与△ABC的位似比为2;
(2)写出△A′B′C′的各顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=3,矩形内部有一动点P满足S△PAB=![]() S矩形ABCD,则点P到A、B两点的距离之和PA+PB的最小值为______.
S矩形ABCD,则点P到A、B两点的距离之和PA+PB的最小值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,求二楼的层高BC约为多少米?( sin42°≈0.7,tan42°≈0.9)

查看答案和解析>>
科目:初中数学 来源: 题型:
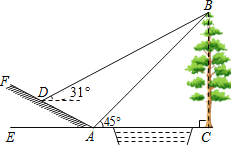
【题目】数学活动课上,小明和小红要测量小河对岸大树BC的高度,小红在点A测得大树顶端B的仰角为45°,小明从A点出发沿斜坡走3![]() 米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2.
米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2.
(1)求小明从点A到点D的过程中,他上升的高度;
(2)依据他们测量的数据能否求出大树BC的高度?若能,请计算;若不能,请说明理由.(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,已知点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() 和
和![]() ,点
,点![]() 为
为![]() 轴正半轴上的一个动点,过点
轴正半轴上的一个动点,过点![]() 、
、![]() 、
、![]() 作
作![]() 的外接圆
的外接圆![]() ,连结
,连结![]() 并延长交圆于点
并延长交圆于点![]() ,连结
,连结![]() 、
、![]() .
.
(1)求证:![]() .
.
(2)当![]() 时,求
时,求![]() 的长度.
的长度.
(3)如图2,连结![]() ,求线段
,求线段![]() 的最小值及当
的最小值及当![]() 最小时
最小时![]() 的外接圆圆心
的外接圆圆心![]() 的坐标.
的坐标.
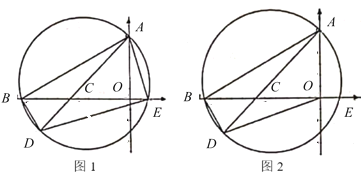
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC 中,AB=AC,点 M 在 BA 的延长线上,点 N 在 BC 的延长线上,过点 C 作CD∥AB 交∠CAM 的平分线于点 D.
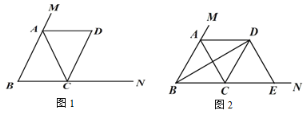
(1)如图 1,求证:四边形 ABCD 是平行四边形;
(2)如图 2,当∠ABC=60°时,连接 BD,过点 D 作 DE⊥BD,交 BN 于点 E,在不添加任何辅助线的情况下,请直接写出图 2 中四个三角形(不包含△CDE),使写出的每个三角形的面积与△CDE 的面积相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
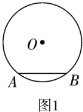
【题目】(1)如图1,![]() 、
、![]() 是
是![]() 上的两个点,点
上的两个点,点![]() 在
在![]() 上,且
上,且![]() 是直角三角形,
是直角三角形,![]() 的半径为1.
的半径为1.
①请在图1中画出点![]() 的位置;
的位置;
②当![]() 时,
时,![]()
![]() ;
;
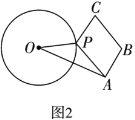
(2)如图2,![]() 的半径为5,
的半径为5,![]() 、
、![]() 为
为![]() 外固定两点(
外固定两点(![]() 、
、![]() 、
、![]() 三点不在同一直线上),且
三点不在同一直线上),且![]() ,
,![]() 为
为![]() 上的一个动点(点
上的一个动点(点![]() 不在直线
不在直线![]() 上),以
上),以![]() 和
和![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,求
,求![]() 最小值并确定此时点
最小值并确定此时点![]() 的位置;
的位置;
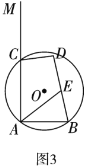
(3)如图3,![]() 、
、![]() 是
是![]() 上的两个点,过
上的两个点,过![]() 点作射线
点作射线![]() ,
,![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,点
,点![]() 是平面内的一个动点,且
是平面内的一个动点,且![]() ,
,![]() 为
为![]() 的中点,在点
的中点,在点![]() 的运动过程中,求线段
的运动过程中,求线段![]() 长度的最大值与最小值.
长度的最大值与最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
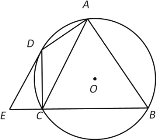
【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,点E在BC的延长线上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AC∥DE,当AB=12,CE=3时,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com