
【题目】对于一元二次方程ax2+bx+c=0(a≠0),下列说法:
①若b=2![]() ,则方程ax2+bx+c=0一定有两个相等的实数根;
,则方程ax2+bx+c=0一定有两个相等的实数根;
②若方程ax2+bx+c=0有两个不等的实数根,则方程x2﹣bx+ac=0也一定有两个不等的实数根;
③若c是方程ax2+bx+c=0的一个根,则一定有ac+b+1=0成立;
④若x0是一元二次方程ax2+bx+c=0的根,则b2﹣4ac=(2ax0+b)2,其中正确的( )
A.只有①②③B.只有①②④C.①②③④D.只有③④
【答案】B
【解析】
判断上述方程的根的情况,只要看根的判别式△![]() 的值的符号就可以了.④难度较大,用到了求根公式表示
的值的符号就可以了.④难度较大,用到了求根公式表示![]() .
.
解:①若![]() ,方程两边平方得b2=4ac,即b2﹣4ac=0,所以方程ax2+bx+c=0一定有两个相等的实数根;
,方程两边平方得b2=4ac,即b2﹣4ac=0,所以方程ax2+bx+c=0一定有两个相等的实数根;
②若方程ax2+bx+c=0有两个不等的实数根,则b2﹣4ac>0
方程x2﹣bx+ac=0中根的判别式也是b2﹣4ac>0,所以也一定有两个不等的实数根;
③若c是方程ax2+bx+c=0的一个根,则一定有ac2+bc+c=0成立,
当c≠0时ac+b+1=0成立;当c=0时ac+b+1=0不成立;
④若x0是一元二次方程ax2+bx+c=0的根,可得![]() ,
,
把x0的值代入(2ax0+b)2,可得b2﹣4ac=(2ax0+b)2,
综上所述其中正确的①②④.
故选:B.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】在△ABC 中,AB=AC,点 M 在 BA 的延长线上,点 N 在 BC 的延长线上,过点 C 作CD∥AB 交∠CAM 的平分线于点 D.
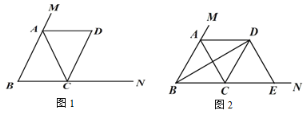
(1)如图 1,求证:四边形 ABCD 是平行四边形;
(2)如图 2,当∠ABC=60°时,连接 BD,过点 D 作 DE⊥BD,交 BN 于点 E,在不添加任何辅助线的情况下,请直接写出图 2 中四个三角形(不包含△CDE),使写出的每个三角形的面积与△CDE 的面积相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校八、九两个年级各有学生180人,为了解这两个年级学生的体质健康情况,进行了抽样调查,具体过程如下:
收集数据
从八、九两个年级各随机抽取20名学生进行体质健康测试,测试成绩(百分制)如下:
八年级 | 78 | 86 | 74 | 81 | 75 | 76 | 87 | 70 | 75 | 90 |
75 | 79 | 81 | 70 | 74 | 80 | 86 | 69 | 83 | 77 | |
九年级 | 93 | 73 | 88 | 81 | 72 | 81 | 94 | 83 | 77 | 83 |
80 | 81 | 70 | 81 | 73 | 78 | 82 | 80 | 70 | 40 |
整理、描述数据
将成绩按如下分段整理、描述这两组样本数据:
成绩(x) | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
八年级人数 | 0 | 0 | 1 | 11 | 7 | 1 |
九年级人数 | 1 | 0 | 0 | 7 | 10 | 2 |
(说明:成绩80分及以上为体质健康优秀,70~79分为体质健康良好,60~69分为体质健康合格,60分以下为体质健康不合格)
分析数据
两组样本数据的平均数、中位数、众数、方差如表所示:
年级 | 平均数 | 中位数 | 众数 | 方差 |
八年级 | 78.3 | 77.5 | 75 | 33.6 |
九年级 | 78 | 80.5 | a | 52.1 |
(1)表格中a的值为______;
(2)请你估计该校九年级体质健康优秀的学生人数为多少?
(3)根据以上信息,你认为哪个年级学生的体质健康情况更好一些?请说明理由.(请从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
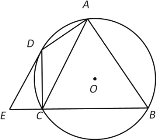
【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,点E在BC的延长线上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AC∥DE,当AB=12,CE=3时,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:若抛物线的顶点在坐标轴上,则称该抛物线为“数轴函数”例如抛物线y=x2和y=(x-1)2都是“数轴函数”.
(1)抛物线y=x2-4x+4和抛物线y=x2-6x是“数轴函数“吗?请说明理由;
(2)若抛物线y=2x2+4mx+m2+16是“数轴函数”,求该抛物线的表达式
查看答案和解析>>
科目:初中数学 来源: 题型:
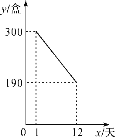
【题目】某公司开发出一款新包装的牛奶,牛奶的成本价为6元/盒,这种新包装的牛奶在正式投放市场前通过代销点进行了为期一个月(30天)的试营销,售价为8元/盒.前几天的销量每况愈下,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的线段表示前12天日销售量y(盒)与销售时间x(天)之间的函数关系,于是从第13天起采用打折销售(不低于成本价),时间每增加1天,日销售量就增加10盒.
(1)打折销售后,第17天的日销售量为________盒;
(2)求y与x之间的函数关系式,并写出x的取值范围;
(3)已知日销售利润不低于560元的天数共有6天,设打折销售的折扣为a折,试确定a的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“作以已知线段为斜边的等腰直角三角形”的尺规作图过程.
已知:线段![]() .
.
![]()
求作:以![]() 为斜边的一个等腰直角三角形
为斜边的一个等腰直角三角形![]() .
.
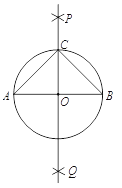
作法:如图,
(1)分别以点![]() 和点
和点![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧相交于
的长为半径作弧,两弧相交于![]() ,
,![]() 两点;
两点;
(2)作直线![]() ,交
,交![]() 于点
于点![]() ;
;
(3)以![]() 为圆心,
为圆心,![]() 的长为半径作圆,交直线
的长为半径作圆,交直线![]() 于点
于点![]() ;
;
(4)连接![]() ,
,![]() .
.
则![]() 即为所求作的三角形.
即为所求作的三角形.
请回答:在上面的作图过程中,①![]() 是直角三角形的依据是________;②
是直角三角形的依据是________;②![]() 是等腰三角形的依据是__________.
是等腰三角形的依据是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学概念
在两个等腰三角形中,如果其中一个三角形的底边长和底角的度数分别等于另一个三角形的腰长和顶角的度数,那么称这两个等腰三角形互为姊妹三角形.
概念理解
(1)如图①,在△ABC中,AB=AC,请用直尺和圆规作出它的姊妹三角形(保留作图痕迹,不写作法).
特例分析
(2)①在△ABC中,AB=AC,∠A=30°,![]() ,求它的姊妹三角形的顶角的度数和腰长;
,求它的姊妹三角形的顶角的度数和腰长;
②如图②,在△ABC中,AB=AC,D是AC上一点,连接BD.若△ABC与△ABD互为姊妹三角形,且△ABC∽△BCD,则∠A= °.
深入研究
(3)下列关于姊妹三角形的结论:
①每一个等腰三角形都有姊妹三角形;
②等腰三角形的姊妹三角形是锐角三角形;
③如果两个等腰三角形互为姊妹三角形,那么这两个三角形可能全等;
④如果一个等腰三角形存在两个不同的姊妹三角形,那么这两个三角形也一定互为姊妹三角形.
其中所有正确结论的序号是 .
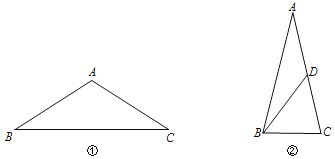
查看答案和解析>>
科目:初中数学 来源: 题型:
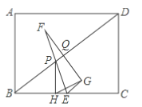
【题目】如图,在矩形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 为对角线
为对角线![]() 上的动点,设
上的动点,设![]() ,作
,作![]() 于点
于点![]() ,连结
,连结![]() 并延长至点
并延长至点![]() ,使得
,使得![]() ,作点
,作点![]() 关于
关于![]() 的对称点
的对称点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() .
.
(1)求证:![]() ;
;
(2)当点![]() 运动到对角线
运动到对角线![]() 的中点时,求
的中点时,求![]() 的周长;
的周长;
(3)在点![]() 的运动的过程中,
的运动的过程中,![]() 是否可以为等腰三角形?若可以,求出
是否可以为等腰三角形?若可以,求出![]() 的值;若不可以,说明理由.
的值;若不可以,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com