
ΓΨΧβΡΩΓΩ ΐ―ßΗ≈Ρν
‘ΎΝΫΗωΒ»―ϋ»ΐΫ«–Έ÷–Θ§»γΙϊΤδ÷–“ΜΗω»ΐΫ«–ΈΒΡΒΉ±Ώ≥ΛΚΆΒΉΫ«ΒΡΕ» ΐΖ÷±πΒ»”ΎΝμ“ΜΗω»ΐΫ«–ΈΒΡ―ϋ≥ΛΚΆΕΞΫ«ΒΡΕ» ΐΘ§Ρ«Ο¥≥Τ’βΝΫΗωΒ»―ϋ»ΐΫ«–ΈΜΞΈΣφΔΟΟ»ΐΫ«–ΈΘ°
Η≈ΡνάμΫβ
Θ®1Θ©»γΆΦΔΌΘ§‘ΎΓςABC÷–Θ§ABΘΫACΘ§«κ”Ο÷±≥ΏΚΆ‘≤ΙφΉς≥ωΥϋΒΡφΔΟΟ»ΐΫ«–ΈΘ®±ΘΝτΉςΆΦΚέΦΘΘ§≤Μ–¥ΉςΖ®Θ©Θ°
ΧΊάΐΖ÷Έω
Θ®2Θ©ΔΌ‘ΎΓςABC÷–Θ§ABΘΫACΘ§ΓœAΘΫ30ΓψΘ§![]() Θ§«σΥϋΒΡφΔΟΟ»ΐΫ«–ΈΒΡΕΞΫ«ΒΡΕ» ΐΚΆ―ϋ≥ΛΘΜ
Θ§«σΥϋΒΡφΔΟΟ»ΐΫ«–ΈΒΡΕΞΫ«ΒΡΕ» ΐΚΆ―ϋ≥ΛΘΜ
ΔΎ»γΆΦΔΎΘ§‘ΎΓςABC÷–Θ§ABΘΫACΘ§D «AC…œ“ΜΒψΘ§Ν§Ϋ”BDΘ°»τΓςABC”κΓςABDΜΞΈΣφΔΟΟ»ΐΫ«–ΈΘ§«“ΓςABCΓΉΓςBCDΘ§‘ρΓœAΘΫΓΓ ΓΓΓψΘ°
…ν»κ―–ΨΩ
Θ®3Θ©œ¬Ν–ΙΊ”ΎφΔΟΟ»ΐΫ«–ΈΒΡΫα¬έΘΚ
ΔΌΟΩ“ΜΗωΒ»―ϋ»ΐΫ«–ΈΕΦ”–φΔΟΟ»ΐΫ«–ΈΘΜ
ΔΎΒ»―ϋ»ΐΫ«–ΈΒΡφΔΟΟ»ΐΫ«–Έ «»ώΫ«»ΐΫ«–ΈΘΜ
Δέ»γΙϊΝΫΗωΒ»―ϋ»ΐΫ«–ΈΜΞΈΣφΔΟΟ»ΐΫ«–ΈΘ§Ρ«Ο¥’βΝΫΗω»ΐΫ«–ΈΩ…Ρή»ΪΒ»ΘΜ
Δή»γΙϊ“ΜΗωΒ»―ϋ»ΐΫ«–Έ¥φ‘ΎΝΫΗω≤ΜΆ§ΒΡφΔΟΟ»ΐΫ«–ΈΘ§Ρ«Ο¥’βΝΫΗω»ΐΫ«–Έ“≤“ΜΕ®ΜΞΈΣφΔΟΟ»ΐΫ«–ΈΘ°
Τδ÷–Υυ”–’ΐ»ΖΫα¬έΒΡ–ρΚ≈ «ΓΓ ΓΓΘ°
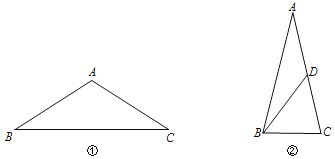
ΓΨ¥πΑΗΓΩΘ®1Θ©ΦϊΫβΈωΘΜΘ®2Θ©ΔΌΓςABCΒΡφΔΟΟ»ΐΫ«–ΈΒΡΕΞΫ«ΈΣ75Γψ ±Θ§―ϋ≥ΛΈΣ![]() ΘΜΕΞΫ«ΈΣ120Γψ ±Θ§―ϋ≥ΛΈΣ
ΘΜΕΞΫ«ΈΣ120Γψ ±Θ§―ϋ≥ΛΈΣ![]() ΘΜΔΎΓœAΘΫΓΓ36ΓΓΓψΘ°Θ®3Θ©Υυ”–’ΐ»ΖΫα¬έΒΡ–ρΚ≈ «ΓΓΔΌΔέΓΓΘ°
ΘΜΔΎΓœAΘΫΓΓ36ΓΓΓψΘ°Θ®3Θ©Υυ”–’ΐ»ΖΫα¬έΒΡ–ρΚ≈ «ΓΓΔΌΔέΓΓΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίφΔΟΟ»ΐΫ«–ΈΒΡΕ®“εΜ≠≥ωΆΦ–ΈΦ¥Ω…ΘΜ
Θ®2Θ©ΔΌΙΐΒψBΉςBGΓΆACΘ§¥ΙΉψΈΣGΘ°…ηBGΘΫxΘ§œκΑλΖ®ΙΙΫ®ΖΫ≥ΧΫβΨωΈ ΧβΦ¥Ω…ΘΜ
ΔΎ Ήœ»÷ΛΟςΓœAΘΫΓœABDΘ§ΓœBDCΘΫΓœCΘΫΓœABCΘ§…ηΓœAΘΫxΘ§άϊ”Ο»ΐΫ«–ΈΡΎΫ«ΚΆΕ®άμΙΙΫ®ΖΫ≥ΧΦ¥Ω…ΫβΨωΈ ΧβΘΜ
Θ®3Θ©ΗυΨίφΔΟΟ»ΐΫ«–ΈΒΡΕ®“ε“Μ“Μ≈–ΕœΦ¥Ω…Θ°
Θ®1Θ©»γΆΦΘ§ΓςDEFΦ¥ΈΣΥυ«σΘ°
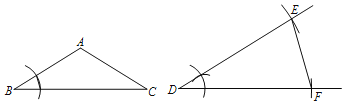
Θ®2Θ©ΔΌ…ηΓςABCΒΡφΔΟΟ»ΐΫ«–ΈΈΣΓςDEFΘ§«“DEΘΫDFΘ°
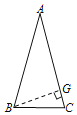
ΓΏ‘ΎΓςABC÷–Θ§ABΘΫACΘ§ΓœAΘΫ30ΓψΘ§BCΘΫ![]() ©¹
©¹![]() Θ§
Θ§
ΓύΓœBΘΫΓœCΘΫ75ΓψΘ§
ΙΐΒψBΉςBGΓΆACΘ§¥ΙΉψΈΣGΘ°…ηBGΘΫxΘ§
‘ρABΘΫACΘΫ2xΘ§AGΘΫ![]() xΘ§
xȧ
ΓύCGΘΫAC©¹AGΘΫ2x©¹![]() xΘΫΘ®2©¹
xΘΫΘ®2©¹![]() Θ©xΘ§
ȩxȧ
‘ΎRtΓςBGC÷–Θ§BG2+CG2ΘΫBC2Θ§
Γύx2+Θ®2©¹![]() Θ©2x2ΘΫΘ®
Θ©2x2ΘΫΘ®![]() ©¹
©¹![]() Θ©2Θ§
Θ©2Θ§
ΓύxΘΫ1Θ§
ΓύABΘΫACΘΫ2Θ°
ΒΎ“Μ÷÷«ι–ΈΘΚΓœDΘΫΓœABCΘΫ75ΓψΘ§
DEΘΫDFΘΫBCΘΫ![]() ©¹
©¹![]() Θ°
Θ°
ΒΎΕΰ÷÷«ι–ΈΘΚΒ±ΓœEΘΫΓœAΘΫ30Γψ ±Θ§ΓœEDFΘΫ120ΓψΘ°
EFΘΫABΘΫ2Θ°
ΙΐΒψDΉςDHΓΆEFΘ§¥ΙΉψΈΣHΘ°
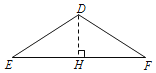
ΓΏDEΘΫDFΘ§ΓύEHΘΫ![]() EFΘΫ1Θ°
EFΘΫ1Θ°
ΓύEDΘΫ![]() Θ§
Θ§
ΓύΓςABCΒΡφΔΟΟ»ΐΫ«–ΈΒΡΕΞΫ«ΈΣ75Γψ ±Θ§―ϋ≥ΛΈΣ![]() ©¹
©¹![]() ΘΜΕΞΫ«ΈΣ120Γψ ±Θ§―ϋ≥ΛΈΣ
ΘΜΕΞΫ«ΈΣ120Γψ ±Θ§―ϋ≥ΛΈΣ![]() ΘΜ
ΘΜ
ΔΎ»γΆΦΔΎ÷–Θ§
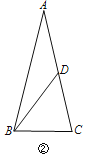
ΓΏΓςABCΓΉΓςBCDΘ§
ΓύΓœAΘΫΓœCBDΘ§ΓœCΘΫΓœBDCΘΫΓœABCΘ§
ΓΏΓςABC”κΓςABDΜΞΈΣφΔΟΟ»ΐΫ«–ΈΘ§
ΓύBCΘΫBDΘ§
ΓΏΓœDBCΘΫΓœA+ΓœABDΘ§ΓœCΘΫΓœABCΘΫΓœDBC+ΓœABDΘ§
ΓύΓœAΘΫΓœABDΘ§…ηΓœAΘΫxΘ§‘ρΓœDBCΘΫxΘ§ΓœBDCΘΫΓœCΘΫ2xΘ§
Γύ5xΘΫ180ΓψΘ§
ΓύxΘΫ36Γψ
Ι ¥πΑΗΈΣΘΚ36ΘΜ
Θ®3Θ©ΔΌΟΩ“ΜΗωΒ»―ϋ»ΐΫ«–ΈΕΦ”–φΔΟΟ»ΐΫ«–ΈΘΜ’ΐ»ΖΘ°
ΔΎΒ»―ϋ»ΐΫ«–ΈΒΡφΔΟΟ»ΐΫ«–Έ «»ώΫ«»ΐΫ«–ΈΘΜ¥μΈσΘ°
Δέ»γΙϊΝΫΗωΒ»―ϋ»ΐΫ«–ΈΜΞΈΣφΔΟΟ»ΐΫ«–ΈΘ§Ρ«Ο¥’βΝΫΗω»ΐΫ«–ΈΩ…Ρή»ΪΒ»ΘΜ’ΐ»ΖΘ°
Δή»γΙϊ“ΜΗωΒ»―ϋ»ΐΫ«–Έ¥φ‘ΎΝΫΗω≤ΜΆ§ΒΡφΔΟΟ»ΐΫ«–ΈΘ§Ρ«Ο¥’βΝΫΗω»ΐΫ«–Έ“≤“ΜΕ®ΜΞΈΣφΔΟΟ»ΐΫ«–ΈΘ°¥μΈσΘ°
Ι ¥πΑΗΈΣΔΌΔέΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ“Μ¥ΈΚ· ΐ![]() ΒΡΆΦœσ”κΖ¥±»άΐΚ· ΐ
ΒΡΆΦœσ”κΖ¥±»άΐΚ· ΐ![]() ΒΡΆΦœσΫΜ”ΎΒψ
ΒΡΆΦœσΫΜ”ΎΒψ![]() Θ§”κ
Θ§”κ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() Θ§»τ
Θ§»τ![]() Θ§«“
Θ§«“![]() .
.
Θ®1Θ©«σΖ¥±»άΐΚ· ΐ”κ“Μ¥ΈΚ· ΐΒΡ±μ¥ο ΫΘΜ
Θ®2Θ©»τΒψ![]() ΈΣx÷α…œ“ΜΒψΘ§
ΈΣx÷α…œ“ΜΒψΘ§![]() «Β»―ϋ»ΐΫ«–ΈΘ§«σΒψ
«Β»―ϋ»ΐΫ«–ΈΘ§«σΒψ![]() ΒΡΉχ±ξ.
ΒΡΉχ±ξ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΕ‘”Ύ“Μ‘ΣΕΰ¥ΈΖΫ≥Χax2+bx+cΘΫ0Θ®aΓΌ0Θ©Θ§œ¬Ν–ΥΒΖ®ΘΚ
ΔΌ»τbΘΫ2![]() Θ§‘ρΖΫ≥Χax2+bx+cΘΫ0“ΜΕ®”–ΝΫΗωœύΒ»ΒΡ Β ΐΗυΘΜ
Θ§‘ρΖΫ≥Χax2+bx+cΘΫ0“ΜΕ®”–ΝΫΗωœύΒ»ΒΡ Β ΐΗυΘΜ
ΔΎ»τΖΫ≥Χax2+bx+cΘΫ0”–ΝΫΗω≤ΜΒ»ΒΡ Β ΐΗυΘ§‘ρΖΫ≥Χx2©¹bx+acΘΫ0“≤“ΜΕ®”–ΝΫΗω≤ΜΒ»ΒΡ Β ΐΗυΘΜ
Δέ»τc «ΖΫ≥Χax2+bx+cΘΫ0ΒΡ“ΜΗωΗυΘ§‘ρ“ΜΕ®”–ac+b+1ΘΫ0≥…ΝΔΘΜ
Δή»τx0 «“Μ‘ΣΕΰ¥ΈΖΫ≥Χax2+bx+cΘΫ0ΒΡΗυΘ§‘ρb2©¹4acΘΫΘ®2ax0+bΘ©2Θ§Τδ÷–’ΐ»ΖΒΡΘ®ΓΓΓΓΘ©
A.÷Μ”–ΔΌΔΎΔέB.÷Μ”–ΔΌΔΎΔήC.ΔΌΔΎΔέΔήD.÷Μ”–ΔέΔή
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ![]() «Β»―ϋ»ΐΫ«–ΈΘ§
«Β»―ϋ»ΐΫ«–ΈΘ§![]() Θ§
Θ§![]() Θ§Βψ
Θ§Βψ![]() ‘Ύ±Ώ
‘Ύ±Ώ![]() …œΘ§Βψ
…œΘ§Βψ![]() ‘Ύ±Ώ
‘Ύ±Ώ![]() …œΘ®Βψ
…œΘ®Βψ![]() ≤Μ”κΥυ‘ΎœΏΕΈΕΥΒψ÷ΊΚœΘ©Θ§
≤Μ”κΥυ‘ΎœΏΕΈΕΥΒψ÷ΊΚœΘ©Θ§![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§…δœΏ
Θ§…δœΏ![]() Θ§―”≥Λ
Θ§―”≥Λ![]() ΫΜ…δœΏ
ΫΜ…δœΏ![]() ”ΎΒψ
”ΎΒψ![]() Θ§Βψ
Θ§Βψ![]() ‘Ύ÷±œΏ
‘Ύ÷±œΏ![]() …œΘ§«“
…œΘ§«“![]() Θ°
Θ°
Θ®1Θ©»γΆΦΘ§Β±![]() ±Θ§«κ÷±Ϋ”–¥≥ω
±Θ§«κ÷±Ϋ”–¥≥ω![]() ”κ
”κ![]() ΒΡΙΊœΒΘΚ_____ΘΜ
ΒΡΙΊœΒΘΚ_____ΘΜ![]() ”κ
”κ![]() ΒΡΈΜ÷ΟΙΊœΒΘΚ_____Θ°
ΒΡΈΜ÷ΟΙΊœΒΘΚ_____Θ°
Θ®2Θ©Β±![]() Θ§ΤδΥϊΧθΦΰ≤Μ±δ ±Θ§
Θ§ΤδΥϊΧθΦΰ≤Μ±δ ±Θ§![]() ΒΡΕ» ΐ «Εύ…ΌΘΩΘ®”ΟΚ§
ΒΡΕ» ΐ «Εύ…ΌΘΩΘ®”ΟΚ§![]() ΒΡ¥ζ ΐ Ϋ±μ ΨΘ©
ΒΡ¥ζ ΐ Ϋ±μ ΨΘ©
Θ®3Θ©»τ![]() «Β»±Ώ»ΐΫ«–ΈΘ§
«Β»±Ώ»ΐΫ«–ΈΘ§![]() Θ§
Θ§![]() «
«![]() ±Ώ…œΒΡ»ΐΒ»Ζ÷ΒψΘ§÷±œΏ
±Ώ…œΒΡ»ΐΒ»Ζ÷ΒψΘ§÷±œΏ![]() ”κ÷±œΏ
”κ÷±œΏ![]() ΫΜ”ΎΒψ
ΫΜ”ΎΒψ![]() Θ§«σœΏΕΈ
Θ§«σœΏΕΈ![]() ΒΡ≥ΛΘ°
ΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
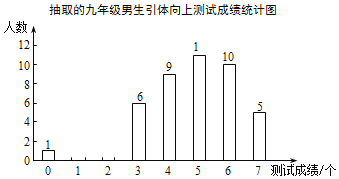
ΓΨΧβΡΩΓΩΡ≥÷–―ßΨ≈ΡξΦΕΡ–…ζΙ≤250»ΥΘ§œ÷ΥφΜζ≥ι»ΓΝΥ≤ΩΖ÷Ψ≈ΡξΦΕΡ–…ζΫχ––“ΐΧεœρ…œ≤β ‘Θ§œύΙΊ ΐΨίΒΡΆ≥ΦΤΆΦ»γœ¬Θ°…η―ß…ζ“ΐΧεœρ…œ≤β ‘≥…Φ®ΈΣxΘ®ΒΞΈΜΘΚΗωΘ©Θ°―ß–ΘΙφΕ®ΘΚΒ±0ΓήxΘΦ2 ±≥…Φ®Β»ΦΕΈΣ≤ΜΦΑΗώΘ§Β±2ΓήxΘΦ4 ±≥…Φ®Β»ΦΕΈΣΦΑΗώΘ§Β±4ΓήxΘΦ6 ±≥…Φ®Β»ΦΕΈΣΝΦΚΟΘ§Β±xΓί6 ±≥…Φ®Β»ΦΕΈΣ”≈–ψΘ°―υ±Ψ÷–“ΐΧεœρ…œ≥…Φ®”≈–ψΒΡ»Υ ΐ’Φ30%Θ§≥…Φ®ΈΣ1ΗωΚΆ2ΗωΒΡ»Υ ΐœύΆ§Θ°
Θ®1Θ©≤Ι»ΪΆ≥ΦΤΆΦΘΜ
Θ®2Θ©ΙάΦΤ»Ϊ–ΘΨ≈ΡξΦΕΡ–…ζ“ΐΧεœρ…œ≤β ‘≤ΜΦΑΗώΒΡ»Υ ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ ΐ÷α…œΒΡΒψAΓΔBΓΔCΓΔDΓΔE±μ ΨΝ§–χΒΡΈεΗω’ϊ ΐΘ§Ε‘”ΠΒΡ ΐΖ÷±πΈΣaΓΔbΓΔcΓΔdΓΔeΓΘ
Θ®1Θ©»τaΘΪeΘΫ0Θ§÷±Ϋ”–¥≥ω¥ζ ΐ ΫbΘΪcΘΪdΒΡ÷ΒΈΣ_____ΘΜ
Θ®2Θ©»τaΘΪbΘΫ7Θ§œ»Μ·ΦρΘ§‘Ό«σ÷ΒΘΚ![]() ΘΜ
ΘΜ
Θ®3Θ©»τaΘΪbΘΪcΘΪdΘΪeΘΫ5Θ§ ΐ÷α…œΒΡΒψM±μ ΨΒΡ Β ΐΈΣmΘ§«“¬ζΉψMAΘΪMEΘΨ12Θ§‘ρmΒΡΖΕΈß «____ΓΘ
![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
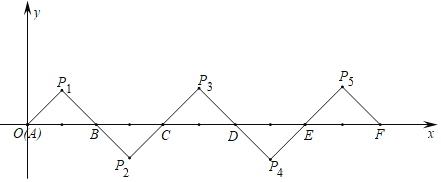
ΓΨΧβΡΩΓΩ»γΆΦΥυ ΨΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() «Β»―ϋ÷±Ϋ«»ΐΫ«–Έ«“
«Β»―ϋ÷±Ϋ«»ΐΫ«–Έ«“![]() Θ§Α―
Θ§Α―![]() »ΤΒψBΥ≥ ±’κ–ΐΉΣ
»ΤΒψBΥ≥ ±’κ–ΐΉΣ![]() Θ§ΒΟΒΫ
Θ§ΒΟΒΫ![]() Θ§Α―
Θ§Α―![]() »ΤΒψCΥ≥ ±’κ–ΐΉΣ
»ΤΒψCΥ≥ ±’κ–ΐΉΣ![]() Θ§ΒΟΒΫ
Θ§ΒΟΒΫ![]() Θ§“ά¥ΥάύΆΤΘ§ΒΟΒΫΒΡΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΒΡ÷±Ϋ«ΕΞΒψ
Θ§“ά¥ΥάύΆΤΘ§ΒΟΒΫΒΡΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΒΡ÷±Ϋ«ΕΞΒψ![]() ΒΡΉχ±ξΈΣ__________Θ°
ΒΡΉχ±ξΈΣ__________Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
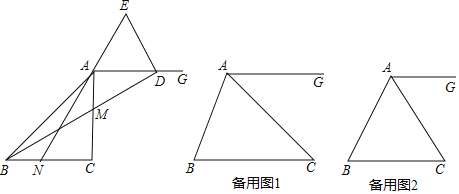
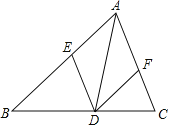
ΓΨΧβΡΩΓΩ»γΆΦAD «ΓςABCΒΡΫ«ΤΫΖ÷œΏΘ§ΙΐΒψDΖ÷±πΉςACΓΔABΒΡΤΫ––œΏΘ§ΫΜAB”ΎΒψEΘ§ΫΜAC”ΎΒψFΘ°
Θ®1Θ©«σ÷ΛΘΚΥΡ±Ώ–ΈAEDF «Νβ–ΈΘ°
Θ®2Θ©»τAFΘΫ13Θ§ADΘΫ24Θ°«σΥΡ±Ώ–ΈAEDFΒΡΟφΜΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
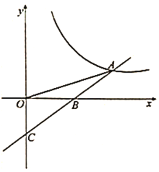
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§÷±œΏl1ΘΚy=©¹![]() x”κΖ¥±»άΐΚ· ΐy=
x”κΖ¥±»άΐΚ· ΐy=![]() ΒΡΆΦœσΫΜ”ΎAΘ§BΝΫΒψΘ®ΒψA‘ΎΒψBΉσ≤ύΘ©Θ§“―÷ΣAΒψΒΡΉίΉχ±ξ «2ΘΚ
ΒΡΆΦœσΫΜ”ΎAΘ§BΝΫΒψΘ®ΒψA‘ΎΒψBΉσ≤ύΘ©Θ§“―÷ΣAΒψΒΡΉίΉχ±ξ «2ΘΚ
Θ®1Θ©«σΖ¥±»άΐΚ· ΐΒΡ±μ¥ο ΫΘΜ
Θ®2Θ©ΫΪ÷±œΏl1ΘΚy=©¹![]() xœρ…œΤΫ“ΤΚσΒΡ÷±œΏl2”κΖ¥±»άΐΚ· ΐy=
xœρ…œΤΫ“ΤΚσΒΡ÷±œΏl2”κΖ¥±»άΐΚ· ΐy=![]() ‘ΎΒΎΕΰœσœόΡΎΫΜ”ΎΒψCΘ§»γΙϊΓςABCΒΡΟφΜΐΈΣ30Θ§«σΤΫ“ΤΚσΒΡ÷±œΏl2ΒΡΚ· ΐ±μ¥ο ΫΘ°
‘ΎΒΎΕΰœσœόΡΎΫΜ”ΎΒψCΘ§»γΙϊΓςABCΒΡΟφΜΐΈΣ30Θ§«σΤΫ“ΤΚσΒΡ÷±œΏl2ΒΡΚ· ΐ±μ¥ο ΫΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com