
【题目】已知![]() 是等腰三角形,
是等腰三角形,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上(点
上(点![]() 不与所在线段端点重合),
不与所在线段端点重合),![]() ,连接
,连接![]() ,射线
,射线![]() ,延长
,延长![]() 交射线
交射线![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 上,且
上,且![]() .
.
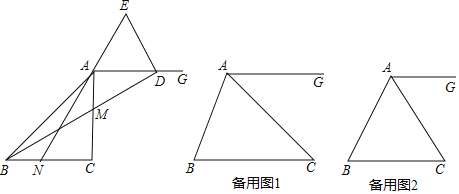
(1)如图,当![]() 时,请直接写出
时,请直接写出![]() 与
与![]() 的关系:_____;
的关系:_____;![]() 与
与![]() 的位置关系:_____.
的位置关系:_____.
(2)当![]() ,其他条件不变时,
,其他条件不变时,![]() 的度数是多少?(用含
的度数是多少?(用含![]() 的代数式表示)
的代数式表示)
(3)若![]() 是等边三角形,
是等边三角形,![]() ,
,![]() 是
是![]() 边上的三等分点,直线
边上的三等分点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() 的长为
的长为![]() 或
或![]()
【解析】
(1)根据SAS证明![]() 即可;根据平行线的性质和余角的性质证明∠ADE+∠ADB=90°即可;
即可;根据平行线的性质和余角的性质证明∠ADE+∠ADB=90°即可;
(2)分两种情形讨论求解即可,①如图2中,当点E在AN的延长线上;②如图3中,当点E在NA的延长线上;结合外角的性质求解;
(3)分两种情形求解即可,①如图4中,当BN=![]() BC=
BC=![]() 时,作AK⊥BC于K,证明△AKN≌△DCF即可得出结论;②如图5中,当CN=
时,作AK⊥BC于K,证明△AKN≌△DCF即可得出结论;②如图5中,当CN=![]() BC=
BC=![]() 时,作AK⊥BC于K,DH⊥BC于H,证明△AKN≌△DHF即可得出结论.
时,作AK⊥BC于K,DH⊥BC于H,证明△AKN≌△DHF即可得出结论.
解:(1)证明:如图1中,∠ACB=90°,
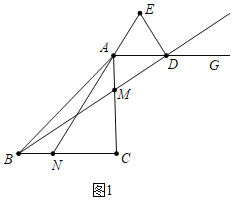
![]() ,
,![]() ,
,
![]()
即![]() ,
,
![]() ,
,
在△BCM和△ACN中,
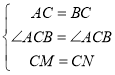 ,
,
![]() (SAS);
(SAS);
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
即BD与DE的位置关系为:BD⊥DE;
(2)解:如图2中,当点![]() 在
在![]() 的延长线上时,
的延长线上时,
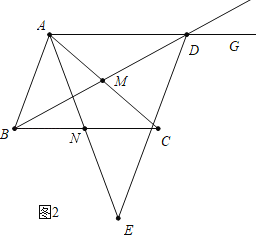
∵AG∥BC,
∠ANB=∠CAN+∠ACB=∠EAD=∠CAN+∠CAD,
∴![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
如图3中,当点![]() 在
在![]() 的延长线上时,
的延长线上时,
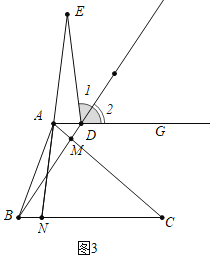
可得![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
综上所述,![]() 或
或![]() .
.
故答案为:![]() 或
或![]() ;
;
(3)解:如图4中,当![]() 时,作
时,作![]() 于
于![]() .
.
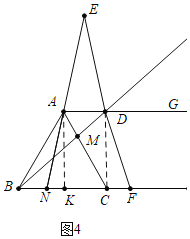
![]() ,
,
![]()
![]() ,
,
![]() =
=![]() BC,
BC,![]() ,
,
∴KC=AD,
∴四边形AKCD为平行四边形,而AK⊥KC,
则四边形![]() 是矩形,
是矩形,
∵AE=DE,
∴∠EAD=∠EDA,
∵AG∥BC,
∴∠EAD=∠ANK=∠DFC=∠EDA,
在△AKN和△DCF中,
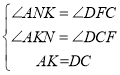
∴△AKN≌△DCF(AAS),
![]() ;
;
如图5中,当![]() 时,作
时,作![]() 于
于![]() ,
,![]() 于
于![]() .
.
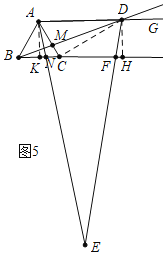
![]() ,
,
![]()
![]() ,
,
![]() ,
,
∵AK⊥AD,DH⊥AD,AG∥BC,
∴四边形AKHD为矩形,
∴AK=DH,AD=KH,
∵△ABC为等边三角形,AK⊥BC,
∴BK=CK=![]() ,
,
∴AK=![]() ,
,
则![]() ,
,
∵AE=DE,
∴∠EAD=∠EDA,
∴∠KAN=∠HDF,
在△AKN和△DHF中,
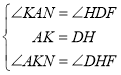 ,
,
∴![]() (ASA),
(ASA),
∴![]() ,
,
![]() .
.
综上所述,![]() 的长为
的长为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
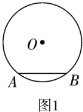
【题目】(1)如图1,![]() 、
、![]() 是
是![]() 上的两个点,点
上的两个点,点![]() 在
在![]() 上,且
上,且![]() 是直角三角形,
是直角三角形,![]() 的半径为1.
的半径为1.
①请在图1中画出点![]() 的位置;
的位置;
②当![]() 时,
时,![]()
![]() ;
;
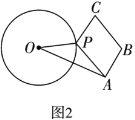
(2)如图2,![]() 的半径为5,
的半径为5,![]() 、
、![]() 为
为![]() 外固定两点(
外固定两点(![]() 、
、![]() 、
、![]() 三点不在同一直线上),且
三点不在同一直线上),且![]() ,
,![]() 为
为![]() 上的一个动点(点
上的一个动点(点![]() 不在直线
不在直线![]() 上),以
上),以![]() 和
和![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,求
,求![]() 最小值并确定此时点
最小值并确定此时点![]() 的位置;
的位置;
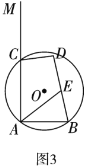
(3)如图3,![]() 、
、![]() 是
是![]() 上的两个点,过
上的两个点,过![]() 点作射线
点作射线![]() ,
,![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,点
,点![]() 是平面内的一个动点,且
是平面内的一个动点,且![]() ,
,![]() 为
为![]() 的中点,在点
的中点,在点![]() 的运动过程中,求线段
的运动过程中,求线段![]() 长度的最大值与最小值.
长度的最大值与最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
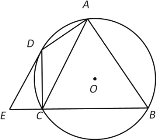
【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,点E在BC的延长线上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AC∥DE,当AB=12,CE=3时,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
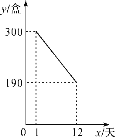
【题目】某公司开发出一款新包装的牛奶,牛奶的成本价为6元/盒,这种新包装的牛奶在正式投放市场前通过代销点进行了为期一个月(30天)的试营销,售价为8元/盒.前几天的销量每况愈下,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的线段表示前12天日销售量y(盒)与销售时间x(天)之间的函数关系,于是从第13天起采用打折销售(不低于成本价),时间每增加1天,日销售量就增加10盒.
(1)打折销售后,第17天的日销售量为________盒;
(2)求y与x之间的函数关系式,并写出x的取值范围;
(3)已知日销售利润不低于560元的天数共有6天,设打折销售的折扣为a折,试确定a的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
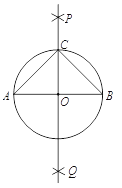
【题目】下面是“作以已知线段为斜边的等腰直角三角形”的尺规作图过程.
已知:线段![]() .
.
![]()
求作:以![]() 为斜边的一个等腰直角三角形
为斜边的一个等腰直角三角形![]() .
.
作法:如图,
(1)分别以点![]() 和点
和点![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧相交于
的长为半径作弧,两弧相交于![]() ,
,![]() 两点;
两点;
(2)作直线![]() ,交
,交![]() 于点
于点![]() ;
;
(3)以![]() 为圆心,
为圆心,![]() 的长为半径作圆,交直线
的长为半径作圆,交直线![]() 于点
于点![]() ;
;
(4)连接![]() ,
,![]() .
.
则![]() 即为所求作的三角形.
即为所求作的三角形.
请回答:在上面的作图过程中,①![]() 是直角三角形的依据是________;②
是直角三角形的依据是________;②![]() 是等腰三角形的依据是__________.
是等腰三角形的依据是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=(x﹣m)2+2(x﹣m)(m为常数)
(1)求证:不论m为何值,该函数的图象与x轴总有两个不同的公共点;
(2)当m取什么值时,该函数的图象关于y轴对称?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学概念
在两个等腰三角形中,如果其中一个三角形的底边长和底角的度数分别等于另一个三角形的腰长和顶角的度数,那么称这两个等腰三角形互为姊妹三角形.
概念理解
(1)如图①,在△ABC中,AB=AC,请用直尺和圆规作出它的姊妹三角形(保留作图痕迹,不写作法).
特例分析
(2)①在△ABC中,AB=AC,∠A=30°,![]() ,求它的姊妹三角形的顶角的度数和腰长;
,求它的姊妹三角形的顶角的度数和腰长;
②如图②,在△ABC中,AB=AC,D是AC上一点,连接BD.若△ABC与△ABD互为姊妹三角形,且△ABC∽△BCD,则∠A= °.
深入研究
(3)下列关于姊妹三角形的结论:
①每一个等腰三角形都有姊妹三角形;
②等腰三角形的姊妹三角形是锐角三角形;
③如果两个等腰三角形互为姊妹三角形,那么这两个三角形可能全等;
④如果一个等腰三角形存在两个不同的姊妹三角形,那么这两个三角形也一定互为姊妹三角形.
其中所有正确结论的序号是 .
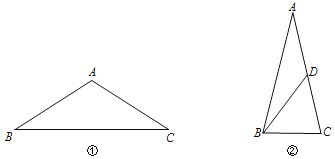
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,图象过
,图象过![]() 点,部分图象如图所示,下列判断:①
点,部分图象如图所示,下列判断:①![]() ;②
;②![]() ;③
;③![]() ;④若点
;④若点![]() ,
,![]() 均在抛物线上,则
均在抛物线上,则![]() ,其中正确的个数是( )
,其中正确的个数是( )
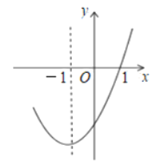
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() .
.
(1)求抛物线的对称轴(用含![]() 的式子去表示);
的式子去表示);
(2)若点![]() ,
,![]() ,
,![]() 都在抛物线
都在抛物线![]() 上,则
上,则![]() 、
、![]() 、
、![]() 的大小关系为_______;
的大小关系为_______;
(3)直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() 与抛物线
与抛物线![]() 有两个交点,在抛物线对称轴右侧的点记为
有两个交点,在抛物线对称轴右侧的点记为![]() ,当
,当![]() 为钝角三角形时,求
为钝角三角形时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com