练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知一次函数的图象与反比例函数的图象交于点，与轴交于点，若，且.

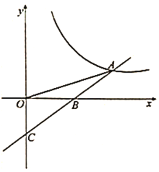
    （1）求反比例函数与一次函数的表达式；

    （2）若点为x轴上一点，是等腰三角形，求点的坐标.

    【答案】（l） ， ；（2）、 ， ，

    【解析】

    （1）根据可计算出A点的纵坐标，进而利用勾股定理计算出A点的横坐标，代入可得一次函数和反比例函数的解析式.

    （2）根据题意可得有三种情况，一种是AB为底，一种是AB为腰，以A为顶点，一种是AB为腰，以B为顶点.

    （l）过点作轴于点

    ∵

    ∴

    ∴

    ∵∴

    在中，

    ∴∴

    ∵经过点 ∴ ∴

    ∴反比例函数表达式为

    ∵经过点，点

    ∴解得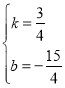

    ∴一次函数表达式为

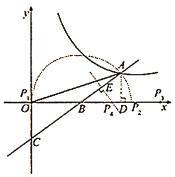
    （2）本题分三种情况

    ①当以为腰，且点为顶角顶点时，可得点的坐标为、

    ②当以为腰，且以点为顶角顶点时，点关于的对称点即为所求的点

    ③当以为底时，作线段的中垂线交轴于点，交于点，则点即为所求

    由（1）得，

    在中，

    ∵

    ∴∴∴∴

    ∴

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

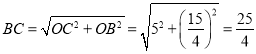
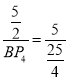    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，AB=4，AD=3，矩形内部有一动点P满足S△PAB=S矩形ABCD，则点P到A、B两点的距离之和PA+PB的最小值为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC 中，AB=AC，点 M 在 BA 的延长线上，点 N 在 BC 的延长线上，过点 C 作CD∥AB 交∠CAM 的平分线于点 D．

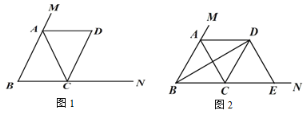
    （1）如图 1，求证：四边形 ABCD 是平行四边形；

    （2）如图 2，当∠ABC=60°时，连接 BD，过点 D 作 DE⊥BD，交 BN 于点 E，在不添加任何辅助线的情况下，请直接写出图 2 中四个三角形（不包含△CDE），使写出的每个三角形的面积与△CDE 的面积相等．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

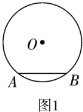
    【题目】（1）如图1，、是上的两个点，点在上，且是直角三角形，的半径为1．

    ①请在图1中画出点的位置；

    ②当时， ；

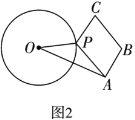
    （2）如图2，的半径为5，、为外固定两点（、、三点不在同一直线上），且，为上的一个动点（点不在直线上），以和为邻边作平行四边形，求最小值并确定此时点的位置；

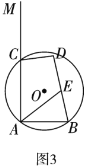
    （3）如图3，、是上的两个点，过点作射线，交于点，若，，点是平面内的一个动点，且，为的中点，在点的运动过程中，求线段长度的最大值与最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

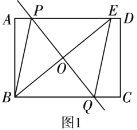
    【题目】（1）如图1，矩形中，点、分别在线段、上，点与点关于对称，点在线段上，连接、、交于点．求证：四边形是菱形；

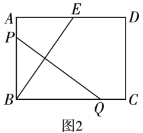
    （2）如图2，矩形中，，点、分别在线段、上，点与点关于对称，点在线段上，，求的长；

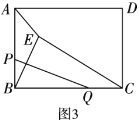
    （3）如图3，有一块矩形空地，，，点是一个休息站且在线段上，，点在线段上，现要在点关于对称的点处修建一口水井，并且修建水渠和，以便于在四边形空地上种植花草，余下部分贴上地砖．种植花草的四边形空地的面积是否存在最小值，若存在，请求出最小值，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校有1500名学生，小明想了解全校学生每月课外阅读书籍的数量情况，随机抽取了部分学生，得到如统计图：

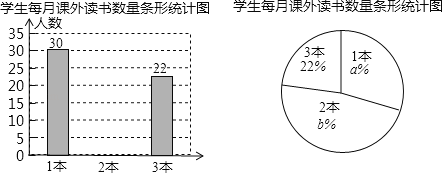
    （1）一共抽查了多少人？

    （2）每月课外阅读书籍数量是1本的学生对应的圆心角度数是多少？

    （3）估计该校全体学生每月课外阅读书籍的总量大约是多少本？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校八、九两个年级各有学生180人，为了解这两个年级学生的体质健康情况，进行了抽样调查，具体过程如下：

    　　收集数据

    从八、九两个年级各随机抽取20名学生进行体质健康测试，测试成绩（百分制）如下：

    八年级

    78

    86

    74

    81

    75

    76

    87

    70

    75

    90

    75

    79

    81

    70

    74

    80

    86

    69

    83

    77

    九年级

    93

    73

    88

    81

    72

    81

    94

    83

    77

    83

    80

    81

    70

    81

    73

    78

    82

    80

    70

    40

    整理、描述数据

    将成绩按如下分段整理、描述这两组样本数据：

    成绩（x）

    40≤x≤49

    50≤x≤59

    60≤x≤69

    70≤x≤79

    80≤x≤89

    90≤x≤100

    八年级人数

    0

    0

    1

    11

    7

    1

    九年级人数

    1

    0

    0

    7

    10

    2

    （说明：成绩80分及以上为体质健康优秀，70～79分为体质健康良好，60～69分为体质健康合格，60分以下为体质健康不合格）

    　　分析数据

    两组样本数据的平均数、中位数、众数、方差如表所示：

    年级

    平均数

    中位数

    众数

    方差

    八年级

    78.3

    77.5

    75

    33.6

    九年级

    78

    80.5

    a

    52.1

    （1）表格中a的值为______；

    （2）请你估计该校九年级体质健康优秀的学生人数为多少？

    （3）根据以上信息，你认为哪个年级学生的体质健康情况更好一些？请说明理由．（请从两个不同的角度说明推断的合理性）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

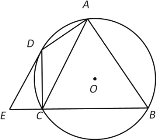
    【题目】如图，四边形ABCD内接于⊙O，∠BAD＝90°，点E在BC的延长线上，且∠DEC＝∠BAC．

    （1）求证：DE是⊙O的切线；

    （2）若AC∥DE，当AB＝12，CE＝3时，求AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数学概念

    在两个等腰三角形中，如果其中一个三角形的底边长和底角的度数分别等于另一个三角形的腰长和顶角的度数，那么称这两个等腰三角形互为姊妹三角形．

    概念理解

    （1）如图①，在△ABC中，AB＝AC，请用直尺和圆规作出它的姊妹三角形（保留作图痕迹，不写作法）．

    特例分析

    （2）①在△ABC中，AB＝AC，∠A＝30°，，求它的姊妹三角形的顶角的度数和腰长；

    ②如图②，在△ABC中，AB＝AC，D是AC上一点，连接BD．若△ABC与△ABD互为姊妹三角形，且△ABC∽△BCD，则∠A＝　 　°．

    深入研究

    （3）下列关于姊妹三角形的结论：

    ①每一个等腰三角形都有姊妹三角形；

    ②等腰三角形的姊妹三角形是锐角三角形；

    ③如果两个等腰三角形互为姊妹三角形，那么这两个三角形可能全等；

    ④如果一个等腰三角形存在两个不同的姊妹三角形，那么这两个三角形也一定互为姊妹三角形．

    其中所有正确结论的序号是　 　．

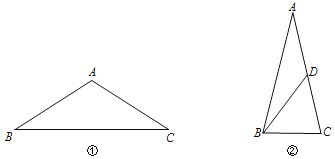
    查看答案和解析>>

    同步练习册答案