
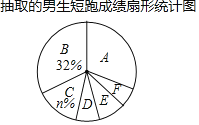
����Ŀ���й������ձ�����6��47���2019�������������������������60�ھ����ձ�����������ܲ��ȳ�ijУΪ�˽��У���꼶�����Ķ���ˮƽ��ȫУ���꼶�����������ȡ�˲��������������ǵĶ���ˮƽ���в��ԣ��������Գɼ�(����10��)���Ƴ����²�������ͳ��ͼ����
��� | �ɼ�/�� | ����/�� |
A | 5 | 36 |
B | 6 | 32 |
C | 7 | 15 |
D | 8 | 8 |
E | 9 | 5 |
F | 10 | m |
�������ͳ��ͼ���е���Ϣ������������⣺
(1)��գ�m��_____��n��_____��
(2)����ȡ�İ��꼶�������ܳɼ���������_____�֣�����ͳ��ͼ��E�������Բ�ĽǵĶ���Ϊ____����
(3)������ȡ�İ��꼶�������ܵ�ƽ���ɼ���
���𰸡���1��4��15��2��5��18��3��6.26
��������
��1������B��32��ռ��������32%����������������m��Ȼ�����C����ռ�İٷֱȼ������n��ֵ��
��2�����������Ķ�������������ɣ����E����ռ�İٷֱȼ�������������ε�Բ�ĽǵĶ�����
��3�����ü�Ȩƽ��������ֱ�Ӽ��㼴�ɣ�
�⣺��1����B�����32�ˣ�ռ32%��
�౻���������Ϊ32��32%��100�ˣ�
��m��100��36��32��15��8��5��4��
15��100��15%��
��n��15��
�ʴ�Ϊ4��15��
��2���ɼ�Ϊ5�ֵ���36�ˣ���࣬
��������Ϊ5�֣�
5��100��360�㣽18�㣬
������ͳ��ͼ��E�������Բ�ĽǵĶ���Ϊ18�㣬
�ʴ�Ϊ5��18��
��3������ȡ�İ��꼶�������ܵ�ƽ���ɼ�Ϊ��![]() ��6.26���֣���
��6.26���֣���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���![]() �У�
��![]() ����
����![]() ��
��![]() �۵�����
�۵�����![]() �Ķ�Ӧ��Ϊ
�Ķ�Ӧ��Ϊ![]() ������
������![]() ��ʹ
��ʹ![]() ƽ��
ƽ��![]() ����
����![]() �����
�����![]() �ǣ� ��
�ǣ� ��
A.![]() ������B.
������B.![]() ������C.
������C.![]() ������D.
������D.![]() ������
������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
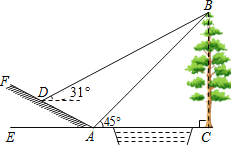
����Ŀ����ѧ����ϣ�С����С��Ҫ����С�Ӷ�����BC�ĸ߶ȣ�С���ڵ�A��ô�������B������Ϊ45����С����A�������б����3![]() ����б���ϵ�D���ڴ˴���������˵�B������Ϊ31������б��AF���±�Ϊ1��2��
����б���ϵ�D���ڴ˴���������˵�B������Ϊ31������б��AF���±�Ϊ1��2��
��1����С���ӵ�A����D�Ĺ����У��������ĸ߶ȣ�
��2���������Dz����������ܷ��������BC�ĸ߶ȣ����ܣ�����㣻�����ܣ���˵�����ɣ����ο����ݣ�sin31���0.52��cos31���0.86��tan31���0.60��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
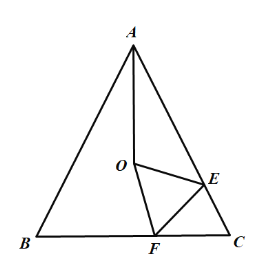
����Ŀ������ABC �У�AB=AC���� M �� BA ���ӳ����ϣ��� N �� BC ���ӳ����ϣ����� C ��CD��AB ����CAM ��ƽ�����ڵ� D��
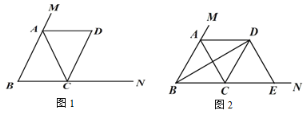
��1����ͼ 1����֤���ı��� ABCD ��ƽ���ı��Σ�
��2����ͼ 2������ABC=60��ʱ������ BD������ D �� DE��BD���� BN �ڵ� E���ڲ������κθ����ߵ�����£���ֱ��д��ͼ 2 ���ĸ������Σ���������CDE����ʹд����ÿ�������ε��������CDE �������ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
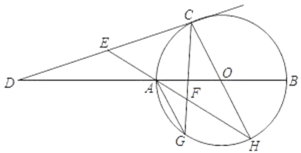
����Ŀ����ͼ����֪ABΪ��O��ֱ����CΪ��O������A��B��һ�㣬��C���������BA���ӳ��߽���D�㣬EΪCD��һ�㣬����EA���ӳ�����O��H��FΪEH��һ�㣬��EF��CE��CF���ӳ��߽���O��G��
��1����֤����AG����GH��
��2����EΪDC���е㣬sim��CDO��![]() ��AH��2
��AH��2![]() �����O�İ뾶��
�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
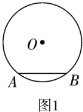
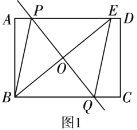
����Ŀ����1����ͼ1��![]() ��
��![]() ��
��![]() �ϵ������㣬��
�ϵ������㣬��![]() ��
��![]() �ϣ���
�ϣ���![]() ��ֱ�������Σ�
��ֱ�������Σ�![]() �İ뾶Ϊ1��
�İ뾶Ϊ1��
������ͼ1�л�����![]() ��λ�ã�
��λ�ã�
�ڵ�![]() ʱ��
ʱ��![]()
![]() ��
��
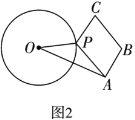
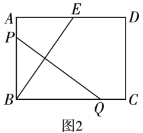
��2����ͼ2��![]() �İ뾶Ϊ5��
�İ뾶Ϊ5��![]() ��
��![]() Ϊ
Ϊ![]() ��̶����㣨
��̶����㣨![]() ��
��![]() ��
��![]() ���㲻��ͬһֱ���ϣ�����
���㲻��ͬһֱ���ϣ�����![]() ��
��![]() Ϊ
Ϊ![]() �ϵ�һ�����㣨��
�ϵ�һ�����㣨��![]() ����ֱ��
����ֱ��![]() �ϣ�����
�ϣ�����![]() ��
��![]() Ϊ�ڱ���ƽ���ı���
Ϊ�ڱ���ƽ���ı���![]() ����
����![]() ��Сֵ��ȷ����ʱ��
��Сֵ��ȷ����ʱ��![]() ��λ�ã�
��λ�ã�
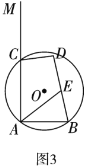
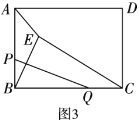
��3����ͼ3��![]() ��
��![]() ��
��![]() �ϵ������㣬��
�ϵ������㣬��![]() ��������
��������![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ����
����![]() ��ƽ���ڵ�һ�����㣬��
��ƽ���ڵ�һ�����㣬��![]() ��
��![]() Ϊ
Ϊ![]() ���е㣬�ڵ�
���е㣬�ڵ�![]() ���˶������У����߶�
���˶������У����߶�![]() ���ȵ����ֵ����Сֵ��
���ȵ����ֵ����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ1������![]() �У���
����![]() ��
��![]() �ֱ����߶�
�ֱ����߶�![]() ��
��![]() �ϣ���
�ϣ���![]() ���
���![]() ����
����![]() �Գƣ���
�Գƣ���![]() ���߶�
���߶�![]() �ϣ�����
�ϣ�����![]() ��
��![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����֤���ı���
����֤���ı���![]() �����Σ�
������
��2����ͼ2������![]() �У�
��![]() ����
����![]() ��
��![]() �ֱ����߶�
�ֱ����߶�![]() ��
��![]() �ϣ���
�ϣ���![]() ���
���![]() ����
����![]() �Գƣ���
�Գƣ���![]() ���߶�
���߶�![]() �ϣ�
�ϣ�![]() ����
����![]() �ij���
�ij���
��3����ͼ3����һ����οյ�![]() ��
��![]() ��
��![]() ����
����![]() ��һ����Ϣվ�����߶�
��һ����Ϣվ�����߶�![]() �ϣ�
�ϣ�![]() ����
����![]() ���߶�
���߶�![]() �ϣ���Ҫ�ڵ�
�ϣ���Ҫ�ڵ�![]() ����
����![]() �ԳƵĵ�
�ԳƵĵ�![]() ����һ��ˮ����������ˮ��
����һ��ˮ����������ˮ��![]() ��
��![]() ���Ա������ı��οյ�
���Ա������ı��οյ�![]() ����ֲ���ݣ����²������ϵ�ש����ֲ���ݵ��ı��οյ�
����ֲ���ݣ����²������ϵ�ש����ֲ���ݵ��ı��οյ�![]() ������Ƿ������Сֵ�������ڣ��������Сֵ���������ڣ���˵�����ɣ�
������Ƿ������Сֵ�������ڣ��������Сֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ�ˡ��������꼶����ѧ��180�ˣ�Ϊ�˽��������꼶ѧ�������ʽ�������������˳������飬����������£�
�����ռ�����
�Ӱˡ��������꼶�������ȡ20��ѧ���������ʽ������ԣ����Գɼ����ٷ��ƣ����£�
���꼶 | 78 | 86 | 74 | 81 | 75 | 76 | 87 | 70 | 75 | 90 |
75 | 79 | 81 | 70 | 74 | 80 | 86 | 69 | 83 | 77 | |
���꼶 | 93 | 73 | 88 | 81 | 72 | 81 | 94 | 83 | 77 | 83 |
80 | 81 | 70 | 81 | 73 | 78 | 82 | 80 | 70 | 40 |
��������������
���ɼ������·ֶ������������������������ݣ�
�ɼ���x�� | 40��x��49 | 50��x��59 | 60��x��69 | 70��x��79 | 80��x��89 | 90��x��100 |
���꼶���� | 0 | 0 | 1 | 11 | 7 | 1 |
���꼶���� | 1 | 0 | 0 | 7 | 10 | 2 |
��˵�����ɼ�80�ּ�����Ϊ���ʽ������㣬70��79��Ϊ���ʽ������ã�60��69��Ϊ���ʽ����ϸ�60������Ϊ���ʽ������ϸ�
������������
�����������ݵ�ƽ��������λ�������������������ʾ��
�꼶 | ƽ���� | ��λ�� | ���� | ���� |
���꼶 | 78.3 | 77.5 | 75 | 33.6 |
���꼶 | 78 | 80.5 | a | 52.1 |
��1��������a��ֵΪ______��
��2��������Ƹ�У���꼶���ʽ��������ѧ������Ϊ���٣�
��3������������Ϣ������Ϊ�ĸ��꼶ѧ�������ʽ����������һЩ����˵�����ɣ������������ͬ�ĽǶ�˵���ƶϵĺ����ԣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
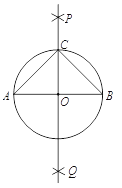
����Ŀ�������ǡ�������֪�߶�Ϊб�ߵĵ���ֱ�������Ρ��ij߹���ͼ���̣�
��֪���߶�![]() ��
��
![]()
��������![]() Ϊб�ߵ�һ������ֱ��������
Ϊб�ߵ�һ������ֱ��������![]() ��
��
��������ͼ��
��1���ֱ��Ե�![]() �͵�
�͵�![]() ΪԲ�ģ�����
ΪԲ�ģ�����![]() �ij�Ϊ�뾶�����������ཻ��
�ij�Ϊ�뾶�����������ཻ��![]() ��
��![]() ���㣻
���㣻
��2����ֱ��![]() ����
����![]() �ڵ�
�ڵ�![]() ��
��
��3����![]() ΪԲ�ģ�
ΪԲ�ģ�![]() �ij�Ϊ�뾶��Բ����ֱ��
�ij�Ϊ�뾶��Բ����ֱ��![]() �ڵ�
�ڵ�![]() ��
��
��4������![]() ��
��![]() ��
��
��![]() ����������������
����������������
��ش����������ͼ�����У���![]() ��ֱ�������ε�������________����
��ֱ�������ε�������________����![]() �ǵ��������ε�������__________��
�ǵ��������ε�������__________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com