
����Ŀ�����������
��1����ͼ������֪�߶�AB��BC��AB��2��BC��5�����߶�AC����СֵΪ�� ����
����̽��
��2����ͼ������֪����COD�У���COD��90�㣬DO��CO��6����A��OC���е㣬�ӳ�OC����F��ʹCF��OC����P��![]() �ϵĶ��㣬��B��OD�ϵ�һ�㣬BD��1��
�ϵĶ��㣬��B��OD�ϵ�һ�㣬BD��1��
��i����֤����OAP����OPF��
��ii����BP+2AP����Сֵ��
��������
��3����ͼ������һ����״Ϊ�ı���ABCD���˹�����BC��9ǧ�ף�CD��4![]() ǧ�ף���BCD��150�㣬�ּƻ��ں���ѡȡһ������һ����ɽP����BP��3ǧ�ף�Ϊ�����ο۹⣬��C��D�ֱ�С��PD��PC����֪����PDÿǧ�������3��Ԫ������PCÿǧ�������1��Ԫ������PD��PC��������Ƿ������Сֵ�������ڣ���ȷ����P��λ�ò��������۵���Сֵ���������ڣ���˵�����ɣ����ŵĿ��Ⱥ��Բ��ƣ�
ǧ�ף���BCD��150�㣬�ּƻ��ں���ѡȡһ������һ����ɽP����BP��3ǧ�ף�Ϊ�����ο۹⣬��C��D�ֱ�С��PD��PC����֪����PDÿǧ�������3��Ԫ������PCÿǧ�������1��Ԫ������PD��PC��������Ƿ������Сֵ�������ڣ���ȷ����P��λ�ò��������۵���Сֵ���������ڣ���˵�����ɣ����ŵĿ��Ⱥ��Բ��ƣ�

���𰸡���1��3����2����i�������������ii��13����3������PD��PC���������СֵΪ12![]() ��Ԫ
��Ԫ
��������
���������
��1������A���߶�BC��ʱ���߶�AC����Сֵ������⣻
����̽��
��2����i��������ɵ�![]() �������������ε��ж��ɵ���OAP����OPF��
�������������ε��ж��ɵ���OAP����OPF��
��ii�������������ε����ʿɵ�PF��2AP���ɵ�BP+2AP��BP+PF��������F����P����B���㹲��ʱ��BP+2AP����Сֵ����СֵΪBF���ɹ��ɶ�������BP+2AP����Сֵ��
��������
��3���Ե�BΪԲ�ģ�3Ϊ�뾶��Բ��AB�ڵ�E����BC�ڵ�F����PΪ![]() ��һ�㣬����BP��PC��PD����BC�Ͻ�ȡBM��1������MD������D��DG��CB����֤��BPM�ס�BCP���ɵ�PC��3PM������P���߶�MD��ʱ������PD��PC�����������Сֵ���ɹ��ɶ�������DM��ֵ����������PD��PC��������Ƿ������Сֵ��
��һ�㣬����BP��PC��PD����BC�Ͻ�ȡBM��1������MD������D��DG��CB����֤��BPM�ס�BCP���ɵ�PC��3PM������P���߶�MD��ʱ������PD��PC�����������Сֵ���ɹ��ɶ�������DM��ֵ����������PD��PC��������Ƿ������Сֵ��
�⣺�����������1���ߵ���A���߶�BC��ʱ���߶�AC����Сֵ��
���߶�AC����Сֵ��5��2��3
�ʴ�Ϊ��3
����̽��
��2����i���ߵ�A��OC���е㣬DO��CO��6��OP��
��![]()
��CF��OC��
��OF��2OC��2OP��
��![]()
��![]() ���ҡ�AOP����FOP
���ҡ�AOP����FOP
���OAP����OPF��
��ii���ߡ�OAP����OPF
��![]()
��PF��2AP
��BP+2AP��BP+PF
�൱��F����P����B���㹲��ʱ��BP+2AP����Сֵ����СֵΪBF
��DO��CO��6��BD��1
��BO��5��OF��12
��BF��![]() ��13
��13
��������
��3����ͼ���Ե�BΪԲ�ģ�3Ϊ�뾶��Բ��AB�ڵ�E����BC�ڵ�F����PΪ![]() ��һ�㣬����BP��PC��PD��
��һ�㣬����BP��PC��PD��
��BC�Ͻ�ȡBM��1������MD������D��DG��CB��
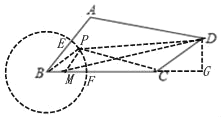
��![]() ���ҡ�PBM����PBC��
���ҡ�PBM����PBC��
���BPM�ס�BCP
��![]()
��PC��3PM
�߽���PD��PC������ۣ�3��PD+1��PC��3PD+��3PM��3��PD+PM��
�൱��P���߶�MD��ʱ������PD��PC�����������Сֵ��
�ߡ�BCD��150��
���DCG��30������DG��BC
��DG��![]() DC��
DC��![]() ��CG��
��CG��![]() DG��6
DG��6
��MG��BC+CG��BM��9+6��1��14
��MD��![]()
�ཨ��PD��PC���������Сֵ��![]() ��Ԫ
��Ԫ


 ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A1A2A3����A3A4A5����A5A6A7����A7A8A9���������ǵ���ֱ�������Σ��ҵ�A1��A3��A5��A7��A9������ֱ�ΪA1 ��3��0����A3 ��1��0����A5 ��4��0����A7 ��0.0����A9 ��5.0��������ͼ������ӳ�Ĺ��ɣ���A102������Ϊ��������

A. ��2��25��B. ��2��26��C. ��![]() ����
����![]() ��D. ��
��D. ��![]() ����
����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����������ij����Ʒʱ��ÿ���ɻ���100Ԫ�������۵İ������۸���Ʒ5���뽫���۽���50Ԫ���۸���Ʒ6�������������.
(1)����Ʒ���ۡ����۷ֱ��Ƕ��٣�
(2)���̳���10000Ԫ���ܽ�������Ʒ��������һ���ڼ��Զ��۵������Ż�ȫ���۳�����ÿ�۳�һ������Ʒʱ��������![]() Ԫ����ḣ����ҵ�����̳�Ϊ�ܻ�ò�����3000Ԫ��������
Ԫ����ḣ����ҵ�����̳�Ϊ�ܻ�ò�����3000Ԫ��������![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ҹ���ȫ������ơ�������������ҹ�����ĸ��2018��5�³ɹ���ɵ�һ�κ�����������.��ͼ����ĸ�������У�����![]() ��ʱ�����С��
��ʱ�����С��![]() λ�����ı�ƫ��
λ�����ı�ƫ��![]() �������뺽ĸ���80����ٺ���һ��ʱ���B�������С��
�������뺽ĸ���80����ٺ���һ��ʱ���B�������С��![]() λ�����ı�ƫ��
λ�����ı�ƫ��![]() ����.�����ĸ����������С��
����.�����ĸ����������С��![]() �����Ϸ����
�����Ϸ����![]() �������躽�еľ���
�������躽�еľ���![]() �ij�.
�ij�.
���ο����ݣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019��3��30�գ��Ĵ�ʡ��ɽ��ľ���ؾ��ڷ���ɭ�ֻ��֣�30�����ҵ��˻�Ӣ�����������˸е�ʹ�ģ�Ҳ�ٴθ����ǵķ���ȫ��ʶ���쾯�ӣ�Ϊ�˼�ǿѧ���ķ���ȫ��ʶ��ijУ������һ�Ρ�����ȫ֪ʶ������������100�֣���������г�ȡ�˲���ѧ���ijɼ����������������������²�������ͳ��ͼ����
��� | �ɼ�x/�� | ����ֵ |
A | 50��x��60 | 55 |
B | 60��x��70 | 65 |
C | 70��x��80 | 75 |
D | 80��x��90 | 85 |
E | 90��x��100 | 95 |
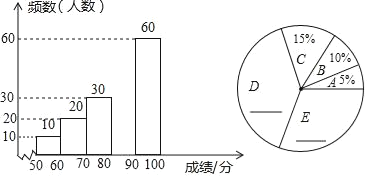
�����ͼ���ṩ����Ϣ��������и��⣺
��1����ȫƵ���ֲ�ֱ��ͼ������ͳ��ͼ��
��2��������80��x��90��Ӧ���ε�Բ�ĽǵĶ������� ���㣬����ȡ��ѧ�������ɼ�����λ�������� �������ڣ�
��3������ÿ�������ֵ�����������˵������ƽ��������������ÿλѧ���ľ����ɼ���������Ƹ�У����ѧ����ƽ���ɼ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
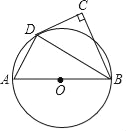
����Ŀ����ͼ��ABΪ��O��ֱ������C�ڡ�O�⣬��ABC��ƽ�������O���ڵ�D����C=90�㣮
��1��CD���O��������λ�ù�ϵ����˵�����ɣ�
��2������CDB=60�㣬AB=6����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���뾶Ϊ2��ԲO�뺬30���ǵ�ֱ�����ǰ�ABC��AB�����ڵ�A����ֱ�����ǰ���BA�����ڵ�ֱ������ƽ�ƣ���ƽ�Ƶ�AC��ԲO����ʱ����ֱ�����ǰ��ƽ�ƾ���Ϊ�� ��
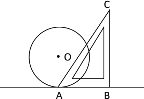
A. ![]() B.
B. ![]() C. 1D. 2
C. 1D. 2![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪CB��CA����ACB��90������D�ڱ�BC�ϣ���B��C���غϣ����ı���ADEFΪ�����Σ�����F��FG��CA����CA���ӳ����ڵ�G������FB����DE�ڵ�Q���ó����½��ۣ���AC��FG����S��FAB��S�ı���CBFG��1��2���ۡ�ABC����ABF����AD2��FQAC��������ȷ���۵ĸ����ǣ�������
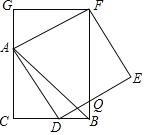
A. 1B. 2C. 3D. 4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com