练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某商场按定价销售某种商品时，每件可获利100元；按定价的八折销售该商品5件与将定价降低50元销售该商品6件所获利润相等.

    (1)该商品进价、定价分别是多少？

    (2)该商场用10000元的总金额购进该商品，并在五一节期间以定价的七折优惠全部售出，在每售出一件该商品时，均捐献元给社会福利事业，该商场为能获得不低于3000元的利润，求的最大值.

    【答案】（1）该商品进价为200元/件，进价为100元/件；（2）10.

    【解析】

    (1)设该商品定价为元/件，进价为元/件，由题意得,解方程组可得；（2）由题意得.

    (1)解法一：设该商品定价为元/件，进价为元/件，由题意得

    解得：

    答：该商品进价为200元/件，进价为100元/件.

    解法二：设该商品进价为元/件，则定价为元/件，由题意得

    解得：

    当时，

    答：该商品进价为200元/件进价为100元/件.

    (2)解：由题意得

    解得：

    的最大值为10.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

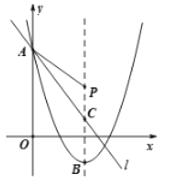
    【题目】如图，已知在平面直角坐标系xOy中，抛物线y=与y轴交于点A，顶点为B，直线l：y=-x+b经过点A，与抛物线的对称轴交于点C，点P是对称轴上的一个动点，若AP+PC的值最小，则点P的坐标为（ ）

    A. （3，1）

    B. （3，）

    C. （3，）

    D. （3，）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在平面直角坐标系中，点A、B、C的坐标分别为（﹣1，3）、（﹣4，1）、（﹣2，1），将△ABC沿一确定方向平移得到△A1B1C1，点B的对应点B1的坐标是（1，2），则点A1，C1的坐标分别是 （　　）

    A. A1（4，4），C1（3，2） B. A1（3，3），C1（2，1）

    C. A1（4，3），C1（2，3） D. A1（3，4），C1（2，2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的。下面是一个案例，请补充完整。

    原题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，试说明理由。

    （1）思路梳理

    ∵AB=CD，

    ∴把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合。

    ∵∠ADC=∠B=90°，

    ∴∠FDG=180°，点F、D、G共线。

    根据　　　　，易证△AFG≌　　　　，得EF=BE+DF。

    （2）类比引申

    如图2，四边形ABCD中，AB=AD，∠BAD=90°，点E、F分别在边BC、CD上，∠EAF=45°。若∠B、∠D都不是直角，则当∠B与∠D满足等量关系　　　　时，仍有EF=BE+DF。

    （3）联想拓展

    如图3，在△ABC中，∠BAC=90°，AB=AC，点D、E均在边BC上，且∠DAE=45°。猜想BD、DE、EC应满足的等量关系，并写出推理过程。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】春晓中学为开展“校园科技节”活动，计划购买A型、B型两种型号的航模．若购买8个A型航模和5个B型航模需用2200元；若购买4个A型航模和6个B型航模需用1520元．求A，B两种型号航模的单价分别是多少元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

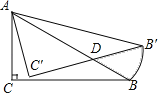
    【题目】已知Rt△ABC中，∠C＝90°，∠ABC＝30°，AC＝1．将Rt△ABC绕点A逆时针旋转15°后，得到Rt△AB'C'，其中点B运动的路径为弧BB'，那么图中阴影部分的面积是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

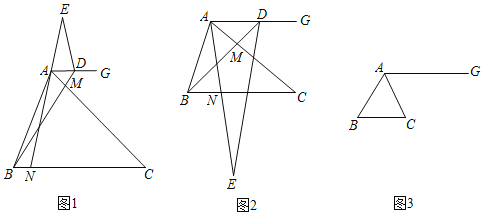
    【题目】已知△ABC中，CA＝CB，0°＜∠ACB≤90°，点M、N分别在边CA，CB上（不与端点重合），BN＝AM，射线AG∥BC交BM延长线于点D，点E在直线AN上，EA＝ED．

    （1）（观察猜想）如图1，点E在射线NA上，当∠ACB＝45°时，①线段BM与AN的数量关系是　 　； ②∠BDE的度数是　 　；

    （2）（探究证明）如图2点E在射线AN上，当∠ACB＝30°时，判断并证明线段BM与AN的数量关系，求∠BDE的度数；

    （3）（拓展延伸）如图3，点E在直线AN上，当∠ACB＝60°时，AB＝3，点N是BC边上的三等分点，直线ED与直线BC交于点F，请直接写出线段CF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题提出：

    （1）如图①，已知线段AB和BC，AB＝2，BC＝5，则线段AC的最小值为　 　；

    问题探究

    （2）如图②，已知扇形COD中，∠COD＝90°，DO＝CO＝6，点A是OC的中点，延长OC到点F，使CF＝OC，点P是 上的动点，点B是OD上的一点，BD＝1．

    （i）求证：△OAP～△OPF；

    （ii）求BP+2AP的最小值；

    问题解决：

    （3）如图③，有一个形状为四边形ABCD的人工湖，BC＝9千米，CD＝4千米，∠BCD＝150°，现计划在湖中选取一处建造一座假山P，且BP＝3千米，为方便游客观光，从C、D分别建小桥PD，PC．已知建桥PD每千米的造价是3万元，建桥PC每千米的造价是1万元，建桥PD和PC的总造价是否存在最小值？若存在，请确定点P的位置并求出总造价的最小值，若不存在，请说明理由．（桥的宽度忽略不计）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，有边长为a的正方形卡片①，边长为b的正方形卡片②，两邻边长分别为a，b的矩形卡片③若干张．

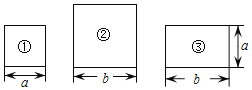
    （1）请用2张卡片①，1张卡片②，3张卡片③拼成一个矩形，在方框中画出这个矩形的草图；

    （2）请结合拼图前后面积之间的关系写出一个等式；

    （3）小明想用类似方法解释多项式乘法（a+3b）（2a+2b）的结果，那么需用卡片①______张，卡片②______张，卡片③______张．

    查看答案和解析>>

    同步练习册答案