
【题目】通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的。下面是一个案例,请补充完整。

原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由。
(1)思路梳理
∵AB=CD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合。
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线。
根据 ,易证△AFG≌ ,得EF=BE+DF。
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°,点E、F分别在边BC、CD上,∠EAF=45°。若∠B、∠D都不是直角,则当∠B与∠D满足等量关系 时,仍有EF=BE+DF。
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°。猜想BD、DE、EC应满足的等量关系,并写出推理过程。
【答案】解:(1)SAS;△AFE。
(2)∠B+∠D=180°。
(3)BD2+EC2=DE2。理由见解析
【解析】
试题(1)在△AFG和△AEF中,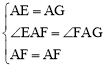 ,∴△AFG≌△AEF(SAS)。
,∴△AFG≌△AEF(SAS)。
(2)如图,把△ABE绕A点逆时针旋转90°至△ADG,可使AB与AD重合,连接FG,

同(1)△AEF≌△AGF(SAS)得EF=GF;
由旋转的性质,得BE=DG,∠B=∠ADG,
若EF=BE+DF,则GF=DG+DF。
∴点F、D、G共线。∴∠ADF+∠ADG180°,即∠B+∠D=180°。
(3)根把△ABD绕A点逆时针旋转90°至△ACG,可使AB与AC重合,根据旋转的性质,全等三角形的性质和勾股定理,可得到BD2+EC2=DE2。
BD2+EC2=DE2。推理过程如下:
∵AB=AC,
∴把△ABD绕A点逆时针旋转90°至△ACG,可使AB与AC重合(如图)。
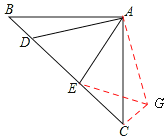
∵△ABC中,∠BAC=90°,
∴∠ACB+∠ACG=∠ACB+∠B=90°,即∠ECG=90°。
∴EC2+CG2=EG2。
在△AEG与△AED中,
∵根据旋转的性质,∠CAG=∠BAD。
∴∠EAG=∠EAC+∠CAG=∠EAC+∠BAD=90°-∠EAD=45°=∠EAD。
又∵根据旋转的性质,AD=AG,AE=AE,
∴△AEG≌△AED(SAS)。∴DE=EG。
又∵CG=BD,∴BD2+EC2=DE2。


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】综合与探究
如图,在平面直角坐标系中,已知抛物线![]() 与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(-2,0),(6,-8).
与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(-2,0),(6,-8).
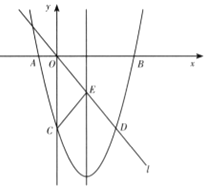
(1)求抛物线的函数表达式,并分别求出点B和点E的坐标;
(2)试探究抛物线上是否存在点F,使![]() ≌
≌![]() ,若存在,请直接写出点F的坐标;若不存在,请说明理由;
,若存在,请直接写出点F的坐标;若不存在,请说明理由;
(3)若点P是y轴负半轴上的一个动点,设其坐标为(0,m),直线PB与直线l交于点Q.试探究:当m为何值时,![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△A1A2A3,△A3A4A5,△A5A6A7,△A7A8A9,…,都是等腰直角三角形,且点A1,A3,A5,A7,A9的坐标分别为A1 (3,0),A3 (1,0),A5 (4,0),A7 (0.0),A9 (5.0),依据图形所反映的规律,则A102的坐标为( )

A. (2,25)B. (2,26)C. (![]() ,﹣
,﹣![]() )D. (
)D. (![]() ,﹣
,﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校随机抽取九年级部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,学校收集整理数据后,将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题:
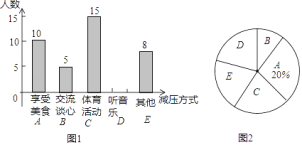
![]() 九年级接受调查的同学共有多少名,并补全条形统计图;
九年级接受调查的同学共有多少名,并补全条形统计图;
![]() 九年级共有500名学生,请你估计该校九年级听音乐减压的学生有多少名;
九年级共有500名学生,请你估计该校九年级听音乐减压的学生有多少名;
![]() 若喜欢“交流谈心”的5名同学中有三名男生和两名女生,心理老师想从5名同学中任选两名同学进行交流,请用画树状图或列表的方法求同时选出的两名同学都是女生的概率.
若喜欢“交流谈心”的5名同学中有三名男生和两名女生,心理老师想从5名同学中任选两名同学进行交流,请用画树状图或列表的方法求同时选出的两名同学都是女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推进“传统文化进校园”活动,某校准备成立“经典诵读”、“传统礼仪”、“民族器乐”和“地方戏曲”等四个课外活动小组.学生报名情况如图(每人只能选择一个小组):
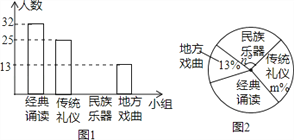
(1)报名参加课外活动小组的学生共有 人,将条形图补充完整;
(2)扇形图中m= ,n= ;
(3)根据报名情况,学校决定从报名“经典诵读”小组的甲、乙、丙、丁四人中随机安排两人到“地方戏曲”小组,甲、乙恰好都被安排到“地方戏曲”小组的概率是多少?请用列表或画树状图的方法说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
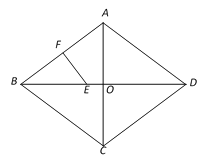
【题目】如图,点O是菱形ABCD对角线的交点,点E在BO上,EF垂直平分AB,垂足为F.
(1)求证:△BEF ∽△DCO;
(2)若AB=10,AC=12,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场按定价销售某种商品时,每件可获利100元;按定价的八折销售该商品5件与将定价降低50元销售该商品6件所获利润相等.
(1)该商品进价、定价分别是多少?
(2)该商场用10000元的总金额购进该商品,并在五一节期间以定价的七折优惠全部售出,在每售出一件该商品时,均捐献![]() 元给社会福利事业,该商场为能获得不低于3000元的利润,求
元给社会福利事业,该商场为能获得不低于3000元的利润,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达![]() 处时,测得小岛
处时,测得小岛![]() 位于它的北偏东
位于它的北偏东![]() 方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛
方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛![]() 位于它的北偏东
位于它的北偏东![]() 方向.如果航母继续航行至小岛
方向.如果航母继续航行至小岛![]() 的正南方向的
的正南方向的![]() 处,求还需航行的距离
处,求还需航行的距离![]() 的长.
的长.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
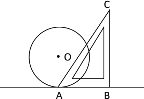
【题目】如图,半径为2的圆O与含30°角的直角三角板ABC的AB边切于点A,将直角三角板沿BA边所在的直线向右平移,当平移到AC与圆O相切时,该直角三角板的平移距离为( )
A. ![]() B.
B. ![]() C. 1D. 2
C. 1D. 2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com