
����Ŀ���ۺ���̽��
��ͼ����ƽ��ֱ������ϵ�У���֪������![]() ��x�ύ��A��B���㣬��y�ύ�ڵ�C��ֱ��l��������ԭ��O���������ߵ�һ������ΪD���������ߵĶԳ��ύ�ڵ�E������CE����֪��A��D������ֱ�Ϊ����2��0������6����8����
��x�ύ��A��B���㣬��y�ύ�ڵ�C��ֱ��l��������ԭ��O���������ߵ�һ������ΪD���������ߵĶԳ��ύ�ڵ�E������CE����֪��A��D������ֱ�Ϊ����2��0������6����8����
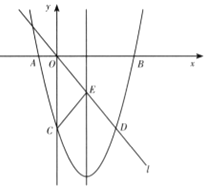
��1���������ߵĺ�������ʽ�����ֱ������B�͵�E�����ꣻ
��2����̽�����������Ƿ���ڵ�F��ʹ![]() ��
��![]() �������ڣ���ֱ��д����F�����ꣻ�������ڣ���˵�����ɣ�
�������ڣ���ֱ��д����F�����ꣻ�������ڣ���˵�����ɣ�
��3������P��y�Ḻ�����ϵ�һ�����㣬��������Ϊ��0��m����ֱ��PB��ֱ��l���ڵ�Q����̽������mΪ��ֵʱ��![]() �ǵ��������Σ�
�ǵ��������Σ�
���𰸡���1��![]() ��B��8,0����E��3��-4������2����
��B��8,0����E��3��-4������2����![]() ����
����![]() ������3��
������3��![]() ��
��![]() .
.
��������
���⣨1����A��D��������뺯������ʽ�����Ԫһ�η��̼��������������ʽ����B���꣺���������߶Գ��ԣ�����Գ�����A�����꼴�����B�����ꣻ��E���꣺EΪֱ��l�������߶Գ���Ľ��㣬����D���������l����ʽ�����������Ϊ![]() �����������E�����ꣻ��2������ȫ�ȶ�Ӧ����ȣ���֪FO=FC�����Ե�F�϶���OC�Ĵ�ֱƽ�����ϣ����Ե�F��������Ϊ-4�����������߱���ʽ��������������ꣻ��3�����ݵ�P��y�Ḻ�������˶�����������������ۣ��ٽ���������.
�����������E�����ꣻ��2������ȫ�ȶ�Ӧ����ȣ���֪FO=FC�����Ե�F�϶���OC�Ĵ�ֱƽ�����ϣ����Ե�F��������Ϊ-4�����������߱���ʽ��������������ꣻ��3�����ݵ�P��y�Ḻ�������˶�����������������ۣ��ٽ���������.
�����������1��![]() ������
������![]() ������A����2��0����D��6����8����
������A����2��0����D��6����8����
![]() ���
���![]()
![]() �����ߵĺ�������ʽΪ
�����ߵĺ�������ʽΪ![]()
![]()
![]() ��
��![]() �����ߵĶԳ���Ϊֱ��
�����ߵĶԳ���Ϊֱ��![]() ����
����![]() ��������x�ύ��A��B���㣬��A������Ϊ����2��0����
��������x�ύ��A��B���㣬��A������Ϊ����2��0����![]() ��B������Ϊ��8��0��
��B��������8��0��
��ֱ��l�ĺ�������ʽΪ![]() ��
��![]() ��D��6����8����ֱ��l�ϣ�
��D��6����8����ֱ��l�ϣ�![]() 6k=��8�����
6k=��8�����![]() ��
��
![]() ֱ��l�ĺ�������ʽΪ
ֱ��l�ĺ�������ʽΪ![]()
![]() ��EΪֱ��l�������߶Գ���Ľ��㣮
��EΪֱ��l�������߶Գ���Ľ��㣮![]() ��E�ĺ�����Ϊ3��������Ϊ
��E�ĺ�����Ϊ3��������Ϊ![]() ��
��
����E��������3����4��
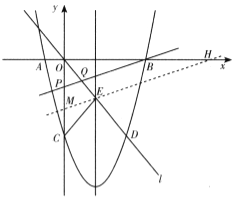
��2���������ϴ��ڵ�F��ʹ![]() ��
��![]() ����F��������
����F��������![]() ����
����![]() ��
��
��3�������������
����![]() ʱ��
ʱ��![]() �ǵ��������Σ�
�ǵ��������Σ�
![]() ��E��������3����4����
��E������Ϊ��3����4����![]() ������E��ֱ��ME//PB����y���ڵ�M����x���ڵ�H����
������E��ֱ��ME//PB����y���ڵ�M����x���ڵ�H����![]() ��
��![]()
![]() ��M��������0����5����
��M��������0����5����
��ֱ��ME�ı���ʽΪ![]() ��
��![]()
![]() �����
�����![]() ��
��![]() ME�ĺ�������ʽΪ
ME�ĺ�������ʽΪ![]() ����y=0����
����y=0����![]() �����x=15��
�����x=15��![]() ��H��������15��0��
��H��������15��0��
��![]() MH//PB��
MH//PB��![]()
![]() ����
����![]() ��
��![]()
![]()
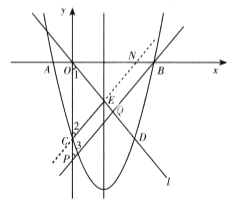
����![]() ʱ��
ʱ��![]() �ǵ��������Σ� ��x=0ʱ��
�ǵ��������Σ� ��x=0ʱ��![]() ��
��![]() ��C��������0����8����
��C��������0����8����
![]()
![]() ��
��![]() OE=CE��
OE=CE��![]()
![]() ������Ϊ
������Ϊ![]() ��
��![]()
![]() ��
��![]()
![]() ��
��![]() CE//PB
CE//PB
��ֱ��CE��x���ڵ�N���亯������ʽΪ![]() ��
��![]()
![]() �����
�����![]() ��
��
![]() CE�ĺ�������ʽΪ
CE�ĺ�������ʽΪ![]() ����y=0����
����y=0����![]() ��
��![]()
![]() ��
��![]() ��N��������6��0��
��N��������6��0��
![]() CN//PB��
CN//PB��![]()
![]() ��
��![]()
![]() �����
�����![]()
������������m��ֵΪ![]() ��
��![]() ʱ��
ʱ��![]() �ǵ��������Σ�
�ǵ��������Σ�


 ����ѵ��ϵ�д�
����ѵ��ϵ�д� ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
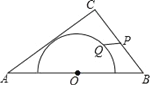
����Ŀ����ͼ���ڡ�ABC�У�AB=10��AC=8��BC=6���Ա�AB���е�OΪԲ�ģ�����Բ��AC���У���P��Q�ֱ��DZ�BC�Ͱ�Բ�ϵĶ��㣬����PQ����PQ������Сֵ��_______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ھ���ABCD�У�E��CD��һ�㣬����P�ӵ�A����������AE��EC��CB�˶�����Bʱֹͣ������Q�ӵ�A��AB�˶�����Bʱֹͣ�����ǵ��ٶȾ�Ϊÿ��1cm�������P��Qͬʱ�ӵ�A����ʼ�˶������˶�ʱ��Ϊx��s������APQ�����Ϊycm2����֪y��x�ĺ���ͼ����ͼ2��ʾ�����½��ۣ���AB��5cm����cos��AED��![]() ������0��x��5ʱ��y��
������0��x��5ʱ��y��![]() ������x��6ʱ����APQ�ǵ��������Σ�����7��x��11ʱ��y��
������x��6ʱ����APQ�ǵ��������Σ�����7��x��11ʱ��y��![]() ��������ȷ���У�������
��������ȷ���У�������
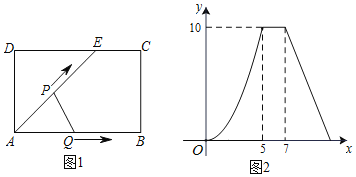
A.2��B.3��C.4��D.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���д�С���ֻ�����3���������4��С����һ�ο����˻�18�֣�2���������6��С����һ�ο����˻�17��.
��1������1���������1��С����һ�ο��Էֱ��˻����ٶ֣�
��2��Ŀǰ��33�ֻ�����Ҫ���䣬���˹�˾�ⰲ�Ŵ�С��������10����ȫ������һ�����꣬����ÿ�������һ���˷ѻ���130Ԫ��ÿ��С����һ���˻�����100Ԫ�����ʻ��˹�˾Ӧ��ΰ��ų������ʡ���ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶��1��������ζԱ���ѧ��������������ϲ���Ŀ������ĵ��飬������������Ϊ�鷨�ͻ滭�ࣨ��ΪA���������ࣨ��ΪB�������ࣨ��ΪC���������ࣨ��ΪD�������ݵ��˽�����ָð�ÿ��ѧ���������˵Ǽ���ÿ��ֻ�Ǽ���һ���Լ���ϲ���Ŀ����������θ��ݵ��������ѧ�������˹��࣬����������������ͳ��ͼ��������ͼ��������Ϣ�������ͬ�⣺
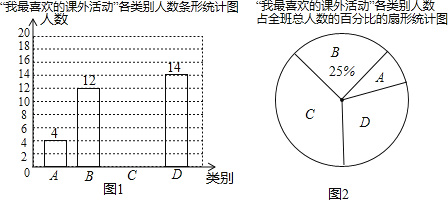
��1�����꼶��1����ѧ��������Ϊ______�ˣ�����ͳ��ͼ��D������Ӧ���ε�Բ�Ľ�Ϊ______�ȣ��벹ȫ����ͳ��ͼ��
��2��ѧУ�������鷨�ͻ滭������ÿ����������ѧ���μӣ�A��4��ѧ����������ѧ���ó��鷨��������ѧ���ó��滭���������ִ�A��4��ѧ���������ȡ����ѧ���μӱ������������б�����״ͼ�ķ�������鵽������ѧ��ǡ����һ���ó��鷨����һ���ó��滭�ĸ��ʣ�
��3�����ȫ����5��������������ôȫ�г������У�ϲ�������ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2017�㽭ʡ�����У���23�⣬10�֣�������������֮��֮�ƣ�ijˮ����ֳ��Ϊ�˸��õط��Ӽ������ƣ�һ�����չ���20000kg��ˮ�㣬�ƻ���ֳһ��ʱ����ٳ��ۣ���֪ÿ������ķ�����ͬ������10����ܳɱ�Ϊ30.4��Ԫ������20����ܳɱ�Ϊ30.8��Ԫ���ܳɱ�=�����ܷ���+�չ��ɱ�����
��1����ÿ��ķ���������a��Ԫ���չ��ɱ�Ϊb��Ԫ����a��b��ֵ��
��2����������ˮ�����t��������Ϊm��kg�������۵���ΪyԪ/kg���������������֪��m��t�ĺ�����ϵΪ![]() ��y��t�ĺ�����ϵ��ͼ��ʾ��
��y��t�ĺ�����ϵ��ͼ��ʾ��
�ٷֱ������0��t��50��50��t��100ʱ��y��t�ĺ�����ϵʽ��
���轫������ˮ�����t���һ���Գ�����������ΪWԪ����tΪ��ֵʱ��W���������ֵ��������=�����ܶ�ܳɱ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ƽ��ֱ������ϵxOy�У�������y=![]() ��y�ύ�ڵ�A������ΪB��ֱ��l��y=-
��y�ύ�ڵ�A������ΪB��ֱ��l��y=-![]() x+b������A���������ߵĶԳ��ύ�ڵ�C����P�ǶԳ����ϵ�һ�����㣬��AP+
x+b������A���������ߵĶԳ��ύ�ڵ�C����P�ǶԳ����ϵ�һ�����㣬��AP+![]() PC��ֵ��С�����P������Ϊ�� ��
PC��ֵ��С�����P������Ϊ�� ��
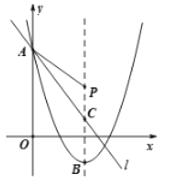
A. ��3��1��
B. ��3��![]() ��
��
C. ��3��![]() ��
��
D. ��3��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����¥AC��һ����һ��б�£�б�µ��½�Ϊ30�㣮С���ڴ�¥��B���������ײ�E���ĸ���Ϊ33�㣬��¥��A���������D���ĸ���Ϊ30�㣮��֪����DE��20m��CE��30m����C��D��E��ͬһƽ���ڣ���A��B����֮��ľ��룮�������ȷ��1m���ο����ݣ�![]() ��1.73��sin33���0.54��cos33���0.84��tan33���0.65��
��1.73��sin33���0.54��cos33���0.84��tan33���0.65��
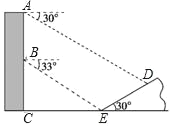
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͨ��������롢������չ�о�������Ŀ���ɴﵽ��һ��֪һ���Ŀ�ġ�������һ���������벹��������

ԭ�⣺��ͼ1����E��F�ֱ���������ABCD�ı�BC��CD�ϣ���EAF=45�㣬����EF����EF=BE+DF����˵�����ɡ�
��1��˼·����
��AB=CD��
������ABE�Ƶ�A��ʱ����ת90������ADG����ʹAB��AD�غϡ�
�ߡ�ADC=��B=90�㣬
���FDG=180�㣬��F��D��G���ߡ�
����������������֤��AFG��������������EF=BE+DF��
��2���������
��ͼ2���ı���ABCD�У�AB=AD����BAD=90������E��F�ֱ��ڱ�BC��CD�ϣ���EAF=45�㡣����B����D������ֱ�ǣ�����B����D���������ϵ��������ʱ������EF=BE+DF��
��3��������չ
��ͼ3������ABC�У���BAC=90�㣬AB=AC����D��E���ڱ�BC�ϣ�����DAE=45�㡣����BD��DE��ECӦ����ĵ�����ϵ����д���������̡�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com