
【题目】(2017浙江省湖州市,第23题,10分)湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了20000kg淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养10天的总成本为30.4万元;放养20天的总成本为30.8万元(总成本=放养总费用+收购成本).
(1)设每天的放养费用是a万元,收购成本为b万元,求a和b的值;
(2)设这批淡水鱼放养t天后的质量为m(kg),销售单价为y元/kg.根据以往经验可知:m与t的函数关系为![]() ;y与t的函数关系如图所示.
;y与t的函数关系如图所示.
①分别求出当0≤t≤50和50<t≤100时,y与t的函数关系式;
②设将这批淡水鱼放养t天后一次性出售所得利润为W元,求当t为何值时,W最大?并求出最大值.(利润=销售总额﹣总成本)

【答案】(1)a的值为0.04,b的值为30;(2)① ;②放养55天时,W最大,最大值为180250元.
;②放养55天时,W最大,最大值为180250元.
【解析】试题分析:(1)由放养10天的总成本为30.4万元;放养20天的总成本为30.8万元可得答案;
(2)①分0≤t≤50、50<t≤100两种情况,结合函数图象利用待定系数法求解可得;
②就以上两种情况,根据“利润=销售总额﹣总成本”列出函数解析式,依据一次函数性质和二次函数性质求得最大值即可得.
试题解析:(1)由题意,得:![]() ,解得:
,解得:![]() ,答:a的值为0.04,b的值为30;
,答:a的值为0.04,b的值为30;
(2)①当0≤t≤50时,设y与t的函数解析式为y=kt+n,将(0,15)、(50,25)代入,得:![]() ,解得:
,解得: ,∴y与t的函数解析式为
,∴y与t的函数解析式为![]() ;
;
当50<t≤100时,设y与t的函数解析式为y=at+b,将点(50,25)、(100,20)代入,得:![]() ,解得:
,解得: ,∴y与t的函数解析式为y=﹣
,∴y与t的函数解析式为y=﹣![]() t+30;
t+30;
综上所述: ;
;
②由题意,当0≤t≤50时,W=20000(![]() t+15)﹣(400t+300000)=3600t,∵3600>0,∴当t=50时,W最大值=180000(元);
t+15)﹣(400t+300000)=3600t,∵3600>0,∴当t=50时,W最大值=180000(元);
当50<t≤100时,W=(100t+15000)(﹣![]() t+30)﹣(400t+300000)
t+30)﹣(400t+300000)
=﹣10t2+1100t+150000
=﹣10(t﹣55)2+180250,∵﹣10<0,∴当t=55时,W最大值=180250(元).
综上所述,放养55天时,W最大,最大值为180250元.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】学生的学业负担过重会严重影响学生对待学习的态度.为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文美书店决定用不多于20000元购进甲乙两种图书共1200本进行销售.甲、乙两种图书的进价分别为每本20元、14元,甲种图书每本的售价是乙种图书每本售价的1.4倍,若用1680元在文美书店可购买甲种图书的本数比用1400元购买乙种图书的本数少10本.
(1)甲乙两种图书的售价分别为每本多少元?
(2)书店为了让利读者,决定甲种图书售价每本降低3元,乙种图书售价每本降低2元,问书店应如何进货才能获得最大利润?(购进的两种图书全部销售完.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与思考:利用多项式的乘法法则,可以得到![]() ,反过来,则有
,反过来,则有![]() 利用这个式子可以将某些二次项系数是1的二次三项式分解因式。例如:将式子
利用这个式子可以将某些二次项系数是1的二次三项式分解因式。例如:将式子![]() 分解因式.这个式子的常数项
分解因式.这个式子的常数项![]() ,一次项系数
,一次项系数![]() ,所以
,所以![]() .
.
解:![]() .
.
上述分解因式![]() 的过程,也可以用十字相乘的形式形象地表示:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数(如图).
的过程,也可以用十字相乘的形式形象地表示:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数(如图).
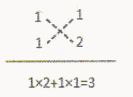
请仿照上面的方法,解答下列问题:
(1)分解因式:![]() ;
;
(2)分解因式:![]() ;
;
(3)若![]() 可分解为两个一次因式的积,写出整数P的所有可能值.
可分解为两个一次因式的积,写出整数P的所有可能值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC、BD相交于点O.下列条件不能判定四边形ABCD为平行四边形的是( )

A. AB∥CD,AD∥BCB. OA=OC,OB=OD
C. AB=CD,AD=BCD. AB∥CD,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区教研部门对本区初二年级的学生进行了一次随机抽样问卷调查,其中有这样一个问题:老师在课堂上放手让学生提问和表达( )
A.从不 B.很少 C.有时 D.常常 E.总是
答题的学生在这五个选项中只能选择一项.下面是根据学生对该问题的答卷情况绘制的两幅不完整的统计图.

根据以上信息,解答下列问题:
(1)该区共有 名初二年级的学生参加了本次问卷调查;
(2)请把这幅条形统计图补充完整;
(3)在扇形统计图中,“总是”的圆心角为 .(精确到度)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的就用了这种分割方法,若BD=2,AE=3,则正方形ODCE的边长等于________.
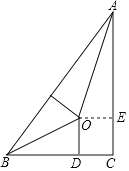
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学完“数据的收集、整理与描述”后,李明对本班期中考试数学成绩(成绩均为整数,满分为150分)作了统计分析(每个人的成绩各不相同,且最低分为50分),绘制成如下频数分布表和频数分布直方图(为避免分数出现在分组的端点处,李明将分点取小数),请你根据图表提供的信息,解答下列问题:
分组 | 频数 | 频率 |
49.5~69.5 | 2 | 0.04 |
69.5~89.5 | 8 |
|
89.5~109.5 | 20 | 0.40 |
109.5~129.5 |
| 0.32 |
129.5~150.5 | 4 | 0.08 |
合计 |
| 1 |

(1)分布表中![]() ______,
______,![]() ______,
______,![]() ______;
______;
(2)补全频数分布直方图;
(3)若画该班期中考试数学成绩的扇形统计图,则分数在89.5~109.5之间的扇形圆心角的度数是____![]() ;
;
(4)张亮同学成绩为109分,他说:“我们班上比我成绩高的人还有![]() ,我要继续努力.”他的说法正确吗?请说明理由.
,我要继续努力.”他的说法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
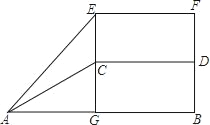
【题目】如图是某个大型商场的自动扶梯侧面示意图,已知自动扶梯AC的坡度为1:2,AC的长度为5![]() 米,AB为底楼地面,CD为二楼侧面,EF为二楼楼顶,当然有EF∥AB∥CD,E为自动扶梯AC的最高端C的正上方,过C的直线EG⊥AB于G,在自动扶梯的底端A测得E的仰角为42°,求该商场二楼的楼高CE.
米,AB为底楼地面,CD为二楼侧面,EF为二楼楼顶,当然有EF∥AB∥CD,E为自动扶梯AC的最高端C的正上方,过C的直线EG⊥AB于G,在自动扶梯的底端A测得E的仰角为42°,求该商场二楼的楼高CE.
(参考数据:sin42°=![]() ,cos42°=
,cos42°=![]() ,tan42°=
,tan42°=![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com