
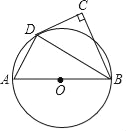
【题目】如图,AB为⊙O的直径,点C在⊙O外,∠ABC的平分线与⊙O交于点D,∠C=90°.
(1)CD与⊙O有怎样的位置关系?请说明理由;
(2)若∠CDB=60°,AB=6,求![]() 的长.
的长.
【答案】(1)相切,理由见解析;(2)π.
【解析】
(1)连接OD,根据BD是∠ABC的平分线的性质有∠CBD=∠ABD,根据OD=OB,得到∠ODB=∠ABD,等量代换得到∠ODB=∠CBD,根据平行线的判定得到OD∥CB,根据平行线的性质有∠ODC=∠C=90°,即可证明CD与⊙O相切;
(2)根据扇形的弧长公式进行计算即可.
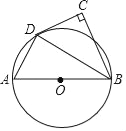
(1)相切.理由如下:
连接OD,
∵BD是∠ABC的平分线,
∴∠CBD=∠ABD,
又∵OD=OB,
∴∠ODB=∠ABD,
∴∠ODB=∠CBD,
∴OD∥CB,
∴∠ODC=∠C=90°,
∴CD与⊙O相切;
(2)若∠CDB=60°,可得∠ODB=30°,
∴∠AOD=60°,
又∵AB=6,
∴AO=3,
∴![]()
![]()


科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,点A、B、C的坐标分别为(﹣1,3)、(﹣4,1)、(﹣2,1),将△ABC沿一确定方向平移得到△A1B1C1,点B的对应点B1的坐标是(1,2),则点A1,C1的坐标分别是 ( )

A. A1(4,4),C1(3,2) B. A1(3,3),C1(2,1)
C. A1(4,3),C1(2,3) D. A1(3,4),C1(2,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
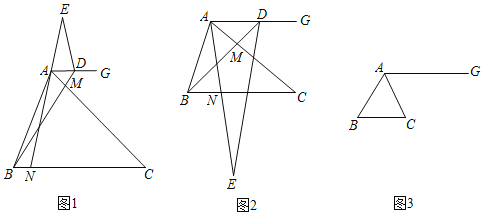
【题目】已知△ABC中,CA=CB,0°<∠ACB≤90°,点M、N分别在边CA,CB上(不与端点重合),BN=AM,射线AG∥BC交BM延长线于点D,点E在直线AN上,EA=ED.
(1)(观察猜想)如图1,点E在射线NA上,当∠ACB=45°时,①线段BM与AN的数量关系是 ; ②∠BDE的度数是 ;
(2)(探究证明)如图2点E在射线AN上,当∠ACB=30°时,判断并证明线段BM与AN的数量关系,求∠BDE的度数;
(3)(拓展延伸)如图3,点E在直线AN上,当∠ACB=60°时,AB=3,点N是BC边上的三等分点,直线ED与直线BC交于点F,请直接写出线段CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:
(1)如图①,已知线段AB和BC,AB=2,BC=5,则线段AC的最小值为 ;
问题探究
(2)如图②,已知扇形COD中,∠COD=90°,DO=CO=6,点A是OC的中点,延长OC到点F,使CF=OC,点P是![]() 上的动点,点B是OD上的一点,BD=1.
上的动点,点B是OD上的一点,BD=1.
(i)求证:△OAP~△OPF;
(ii)求BP+2AP的最小值;
问题解决:
(3)如图③,有一个形状为四边形ABCD的人工湖,BC=9千米,CD=4![]() 千米,∠BCD=150°,现计划在湖中选取一处建造一座假山P,且BP=3千米,为方便游客观光,从C、D分别建小桥PD,PC.已知建桥PD每千米的造价是3万元,建桥PC每千米的造价是1万元,建桥PD和PC的总造价是否存在最小值?若存在,请确定点P的位置并求出总造价的最小值,若不存在,请说明理由.(桥的宽度忽略不计)
千米,∠BCD=150°,现计划在湖中选取一处建造一座假山P,且BP=3千米,为方便游客观光,从C、D分别建小桥PD,PC.已知建桥PD每千米的造价是3万元,建桥PC每千米的造价是1万元,建桥PD和PC的总造价是否存在最小值?若存在,请确定点P的位置并求出总造价的最小值,若不存在,请说明理由.(桥的宽度忽略不计)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,BC与⊙O相切于点B,CD与⊙O相切于点D,连结AD.
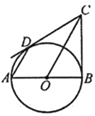
(1)求证:AD∥OC.
(2)小聪与小明在做这个题目的时候,对∠CDA与∠AOC之间的关系进行了探究:
小聪说,∠CDA+∠AOC的值是一个固定的值;
小明说,∠CDA+∠AOC的值随∠A度数的变化而变化.
若∠CDA+∠AOC的值为y,∠A度数为x.你认为他们之中谁说的是正确的?若你认为小聪说的正确,请你求出这个固定值:若你认为小明说的正确,请你求出y与x之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
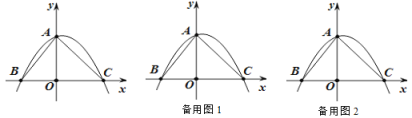
【题目】如图,抛物线y=ax2+bx+4(a≠0)与![]() 轴交于点B (-3 ,0) 和C (4 ,0)与
轴交于点B (-3 ,0) 和C (4 ,0)与![]() 轴交于点A.
轴交于点A.
(1) a = ,b = ;
(2) 点M从点A出发以每秒1个单位长度的速度沿AB向B运动,同时,点N从点B出发以每秒1个单位长度的速度沿BC向C运动,当点M到达B点时,两点停止运动.t为何值时,以B、M、N为顶点的三角形是等腰三角形?
(3) 点P是第一象限抛物线上的一点,若BP恰好平分∠ABC,请直接写出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标中,抛物线y=ax2+bx+c过点A(﹣1,0),B(3,0),C(0,3),点P是直线BC上方抛物线上的一动点,PE∥y轴,交直线BC于点E连接AP,交直线BC于点 D.
(1)求抛物线的函数表达式;
(2)当AD=2PD时,求点P的坐标;
(3)求线段PE的最大值;
(4)当线段PE最大时,若点F在直线BC上且∠EFP=2∠ACO,直接写出点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有边长为a的正方形卡片①,边长为b的正方形卡片②,两邻边长分别为a,b的矩形卡片③若干张.
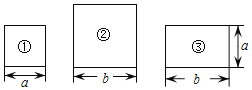
(1)请用2张卡片①,1张卡片②,3张卡片③拼成一个矩形,在方框中画出这个矩形的草图;
(2)请结合拼图前后面积之间的关系写出一个等式;
(3)小明想用类似方法解释多项式乘法(a+3b)(2a+2b)的结果,那么需用卡片①______张,卡片②______张,卡片③______张.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PQMN的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ.过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=![]() DQ,求点F的坐标.
DQ,求点F的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com